Note: I have not checked this thoroughly.
数学中最熟悉的实体 之一是数字 。从学龄前到高级水平,数字 与数学息息相关。但在数学上,这些数字 是什么?本节将展示数学家如何构建数系。我们将从集合论的公理(ZFC 集合论)开始,并以纯粹的集合论方法来构建数字 。
N {\displaystyle \mathbb {N} } [ 编辑 | 编辑源代码 ] 有了这些公理,我们就可以开始构建数字。我们的重点是快速启动并构建所有常用的数字。因此,我们不会专注于开发集合所具有的所有属性,而是相信用户会同意我们的构造足够健全,并且所有属性的严格证明都确实存在于这些公理中。
我们的第一个目标是构建基本的计数数字,也称为自然数。无穷公理说存在一个集合X ,它满足包含空集和集合的属性,以及当一个集合y 是X 的成员时, S ( y ) {\displaystyle S(y)\!} X 的成员。可能存在也可能不存在其他此类集合。取所有此类集合的交集,我们得到自然数集N 。显然,它是最小集合。同样,由于 ∅ {\displaystyle \varnothing } N 的成员,因此是, { ∅ } {\displaystyle \{\varnothing \}} { ∅ { ∅ } } {\displaystyle \{\varnothing \,\{\varnothing \}\}} N 是最小的集合。我们令 0 = ∅ {\displaystyle 0=\varnothing } 1 = { ∅ } {\displaystyle 1=\{\varnothing \}} 2 = { ∅ { ∅ } } {\displaystyle 2=\{\varnothing \,\{\varnothing \}\}}
因此,我们从数学上定义了自然数集。我们将如下定义自然数的加法和乘法:令 x + = S ( x ) {\displaystyle x^{+}=S(x)\!} a + ( b + ) = ( a + b ) + {\displaystyle a+(b^{+})=(a+b)^{+}} 1 + 1 = 1 + 0 + = ( 1 + 0 ) + = 1 + = 2 {\displaystyle 1+1=1+0^{+}=(1+0)^{+}=1^{+}=2} 0 + = 1 {\displaystyle 0^{+}=1}
我们再次假设读者信任我们,当我们说所有自然数的通常性质都可以在我们构建的自然数系统中建立时,我们再次迈出了一步。我们在这里避免这样做是因为我们希望避免陷入正式论证,并偏离我们的目标,即快速地对数字进行数学构建。
接下来我们处理整数。由于我们需要在我们的工具箱中使用一些简短的无关概念(所有这些概念都是根据集合论公理定义的,并且它们的性质也与之一致),我们将简要提到这些概念。首先是序偶 (a,b) 的概念,它被定义为集合 {{a},{a,b}},使用它可以定义 3 元组 (a,b,c) 为序偶 (a,(b,c)),即 {{a}{{b},{b,c}}}。类似地,可以定义 4 元组、5 元组等。接下来是函数和关系的概念,我们相信读者从微积分中了解这些概念。最后,我们讨论等价关系和等价类。
给定集合 *A* 上的一个关系 ~ 被称为等价关系,当且仅当它具有自反性、对称性和传递性。等价地,对于 *A* 中的所有 *a*、*b* 和 *c*,
*a* ~ *a*。(自反性)
如果 *a* ~ *b*,则 *b* ~ *a*。(对称性)
如果 *a* ~ *b* 且 *b* ~ *c*,则 *a* ~ *c*。(传递性) *a* 在 ~ 下的等价类,记为 [*a*],被定义为 [ a ] = { b ∈ A | a ∼ b } {\displaystyle [a]=\{b\in A|a\sim b\}}
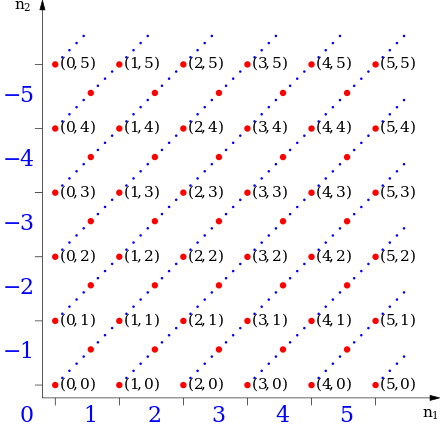
红点表示自然数的有序对。连接的红点是等价类,表示线末端的蓝色整数。 现在,整数集可以正式定义为特定关系的等价类集。该关系是在自然数的有序对之间定义的(不是在自然数本身之间,而是在它们的对之间)。
直觉是 ( *a*,*b* ) 代表从 *a* 中减去 *b* 的结果。为了证实我们的预期,即1 − 2 和4 − 5 表示同一个数字,我们根据以下规则在这些对上定义了一个等价关系 ~
( a , b ) ∼ ( c , d ) {\displaystyle (a,b)\sim (c,d)\,\!} 当且仅当
a + d = b + c . {\displaystyle a+d=b+c.\,\!} 整数的加法和乘法可以根据自然数上的等效运算来定义;用 [( *a*,*b* )] 表示包含 ( *a*,*b* ) 作为成员的等价类,我们有
[ ( a , b ) ] + [ ( c , d ) ] := [ ( a + c , b + d ) ] . {\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].\,} [ ( a , b ) ] ⋅ [ ( c , d ) ] := [ ( a c + b d , a d + b c ) ] . {\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].\,} 整数的否定(或加法逆元)是通过颠倒对的顺序获得的
− [ ( a , b ) ] := [ ( b , a ) ] . {\displaystyle -[(a,b)]:=[(b,a)].\,} 因此,减法可以定义为加法逆元的加法
[ ( a , b ) ] − [ ( c , d ) ] := [ ( a + d , b + c ) ] . {\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].\,} 整数的标准排序由以下给出
[ ( a , b ) ] < [ ( c , d ) ] {\displaystyle [(a,b)]<[(c,d)]\,} a + d < b + c . {\displaystyle a+d<b+c.\,} 很容易验证这些定义与等价类代表的选择无关。
每个等价类都有一个唯一的成员,其形式为 (n ,0) 或 (0,n )(或两者兼有)。自然数 n 与类 [(n ,0)] 识别(换句话说,自然数被嵌入到整数中,通过将 n 映射到 [(n ,0)]),而类 [(0,n )] 被表示为 −n (这涵盖了所有剩余的类,并且为类 [(0,0)] 提供了第二个时间,因为 −0 = 0。)
因此,[(a ,b )] 被表示为
{ a − b , if a ≥ b − ( b − a ) , if a < b . {\displaystyle {\begin{cases}a-b,&{\mbox{if }}a\geq b\\-(b-a),&{\mbox{if }}a<b.\end{cases}}} 如果自然数被识别为相应的整数,这种约定不会产生歧义。
这种表示法恢复了整数的熟悉表示法,即 {... −3,−2,−1, 0, 1, 2, 3, ...}。
一些例子是
0 = [ ( 0 , 0 ) ] = [ ( 1 , 1 ) ] = ⋯ = [ ( k , k ) ] 1 = [ ( 1 , 0 ) ] = [ ( 2 , 1 ) ] = ⋯ = [ ( k + 1 , k ) ] − 1 = [ ( 0 , 1 ) ] = [ ( 1 , 2 ) ] = ⋯ = [ ( k , k + 1 ) ] 2 = [ ( 2 , 0 ) ] = [ ( 3 , 1 ) ] = ⋯ = [ ( k + 2 , k ) ] − 2 = [ ( 0 , 2 ) ] = [ ( 1 , 3 ) ] = ⋯ = [ ( k , k + 2 ) ] . {\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}} 下一站:有理数!
那些学习过代数课程的人可能会认识到下面的构造,正是通过这种构造,一个整环被嵌入到一个域中。(事实上,这并不奇怪,因为整数形成一个整环,而有理数形成一个域。)对于那些认为域是开阔空间,并且在考虑农业而不是农业的人来说,不用担心。我们在下面提供了完整的构造。
一个图表,显示了整数对等价类的表示 在数学上,构造类似于我们从自然数构造整数时所做的。我们考虑所有整数有序对 (m ,n ) 之间的以下关系,其中 n ≠ 0。具体来说,关系是 (m 1 ,n 1 ) ~ (m 2 ,n 2 ) 当且仅当 m 1 n 2 − m 2 n 1 = 0。
( m 1 , n 1 ) + ( m 2 , n 2 ) := ( m 1 n 2 + n 1 m 2 , n 1 n 2 ) {\displaystyle \left(m_{1},n_{1}\right)+\left(m_{2},n_{2}\right):=\left(m_{1}n_{2}+n_{1}m_{2},n_{1}n_{2}\right)} ( m 1 , n 1 ) × ( m 2 , n 2 ) := ( m 1 m 2 , n 1 n 2 ) {\displaystyle \left(m_{1},n_{1}\right)\times \left(m_{2},n_{2}\right):=\left(m_{1}m_{2},n_{1}n_{2}\right)} 并且,如果 m 2 ≠ 0,则除以
( m 1 , n 1 ) ( m 2 , n 2 ) := ( m 1 n 2 , n 1 m 2 ) . {\displaystyle {\frac {\left(m_{1},n_{1}\right)}{\left(m_{2},n_{2}\right)}}:=\left(m_{1}n_{2},n_{1}m_{2}\right).} 等价关系 (m 1 ,n 1 ) ~ (m 2 ,n 2 ) 当且仅当 m 1 n 2 − m 2 n 1 = 0Q 为该关系下所有等价类的集合。我们用 [(m 1 ,n 1 )] 表示包含 (m 1 ,n 1 ) 的等价类。如果 (m 1 ,n 1 ) ~ (m 2 ,n 2 ),则根据定义,(m 1 ,n 1 ) 属于 [(m 2 ,n 2 )],而 (m 2 ,n 2 ) 属于 [(m 1 ,n 1 )];在这种情况下,我们可以写 [(m 1 ,n 1 )] = [(m 2 ,n 2 )]。对于任何等价类 [(m ,n )],都有无穷多个表示形式,因为
⋯ = [ ( − 2 m , − 2 n ) ] = [ ( − m , − n ) ] = [ ( m , n ) ] = [ ( 2 m , 2 n ) ] = ⋯ . {\displaystyle \cdots =[(-2m,-2n)]=[(-m,-n)]=[(m,n)]=[(2m,2n)]=\cdots .} [(m ,n )] 的规范选择是使 gcd(m ,n ) = 1,即 m 和 n 没有公因子,即 m 和 n 互质。例如,我们会写 [(1,2)] 而不是 [(2,4)] 或 [(−12,−24)],即使 [(1,2)] = [(2,4)] = [(−12,−24)]。
整数可以通过将 m 映射到 [(m , 1)] 的嵌入被视为有理数。
实数在等着我们!
首先,我们需要德德金分割的概念。德德金分割,以理查德·德德金命名,是有理数的一个划分,将其分成两个非空部分 A 和 B,使得 A 中的所有元素都小于 B 中的所有元素,并且 A 不包含最大元素。分割本身在概念上是 A 和 B 之间定义的“间隙”。换句话说,A 包含所有小于分割的有理数,而 B 包含所有大于分割的有理数。
为了方便起见,我们可以将较低集合 A 作为任何给定德德金分割 A,B 的代表,因为 A 完全决定了 B。我们现在定义实数集为所有德德金分割的集合。更详细地说,一个实数 r {\displaystyle r} Q {\displaystyle {\textbf {Q}}}
r {\displaystyle r} r ≠ Q {\displaystyle r\neq {\textbf {Q}}} r 向下闭合。换句话说,对于所有 x , y ∈ Q {\displaystyle x,y\in {\textbf {Q}}} x < y {\displaystyle x<y} y ∈ r {\displaystyle y\in r} x ∈ r {\displaystyle x\in r} r 没有最大元素。换句话说,不存在 x ∈ r {\displaystyle x\in r} y ∈ r {\displaystyle y\in r} y ≤ x {\displaystyle y\leq x} 我们形成实数集 R {\displaystyle {\textbf {R}}} Q {\displaystyle {\textbf {Q}}} A {\displaystyle A} 我们将有理数嵌入到实数中,通过将有理数 q {\displaystyle q} { x ∈ Q : x < q } {\displaystyle \{x\in {\textbf {Q}}:x<q\}} 加法。 A + B := { a + b : a ∈ A ∧ b ∈ B } {\displaystyle A+B:=\{a+b:a\in A\land b\in B\}} 定义乘法就不那么直接了。如果 A , B ≥ 0 {\displaystyle A,B\geq 0} A × B := { a × b : a ≥ 0 ∧ a ∈ A ∧ b ≥ 0 ∧ b ∈ B } ∪ { x ∈ Q : x < 0 } {\displaystyle A\times B:=\{a\times b:a\geq 0\land a\in A\land b\geq 0\land b\in B\}\cup \{x\in \mathrm {Q} :x<0\}}
如果 A {\displaystyle A\,} B {\displaystyle B\,} A × B = − ( A × − B ) = − ( − A × B ) = ( − A × − B ) {\displaystyle A\times B=-(A\times -B)=-(-A\times B)=(-A\times -B)\,} A {\displaystyle A\,} B {\displaystyle B\,} 我们做完了吗?还没有。读者无疑已经遇到的复数集还在等待我们。幸运的是,它不需要像实数那样详细的展开,我们很快就可以得到它,方法如下。
设 C 为实数的有序对 (a , b ) 的集合 R 2 。C 被定义为复数集。在这种表示法中,加法和乘法的上述公式写为
( a , b ) + ( c , d ) = ( a + c , b + d ) {\displaystyle (a,b)+(c,d)=(a+c,b+d)\,} ( a , b ) ⋅ ( c , d ) = ( a c − b d , b c + a d ) {\displaystyle (a,b)\cdot (c,d)=(ac-bd,bc+ad)\,} 然后,将 (a, b) 表示为 a + ib 仅仅是一个符号问题。加法和乘法是自然定义的。
← 关系 · 排序 →














![{\displaystyle [a]=\{b\in A|a\sim b\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecd447db4dc0435369173860cd769d704aab0a86)


![{\displaystyle [(a,b)]+[(c,d)]:=[(a+c,b+d)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfcba304a40eefc1e283a196d969ce6fa683cceb)
![{\displaystyle [(a,b)]\cdot [(c,d)]:=[(ac+bd,ad+bc)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7fd52f4eb8780650b373d9344ef67d9d7dbd82aa)
![{\displaystyle -[(a,b)]:=[(b,a)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d87f0da3470a1aa6e060178fe742c78a559c72f4)
![{\displaystyle [(a,b)]-[(c,d)]:=[(a+d,b+c)].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6c83020bdeb7849794e886ea622e66a1dd4ae76)
![{\displaystyle [(a,b)]<[(c,d)]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b572331cb7640ad3bb18ece2afea1a790b27a3eb)


![{\displaystyle {\begin{aligned}0&=[(0,0)]&=[(1,1)]&=\cdots &&=[(k,k)]\\1&=[(1,0)]&=[(2,1)]&=\cdots &&=[(k+1,k)]\\-1&=[(0,1)]&=[(1,2)]&=\cdots &&=[(k,k+1)]\\2&=[(2,0)]&=[(3,1)]&=\cdots &&=[(k+2,k)]\\-2&=[(0,2)]&=[(1,3)]&=\cdots &&=[(k,k+2)].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/325c6a83a84e4fe08bac03e453f674b1ff83eac1)



![{\displaystyle \cdots =[(-2m,-2n)]=[(-m,-n)]=[(m,n)]=[(2m,2n)]=\cdots .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e24a266d671aacfa9b28f50c572f733d630b72c)



















