信号处理/模拟滤波器

模拟滤波器

从历史上看，电信号处理始于模拟电路。信号分析和滤波器设计方法最初基于这类电路。后来出现了数字系统。第一个数字滤波器依赖于它们模拟父滤波器的技术。直到今天，一些数字滤波器仍然依赖于模拟滤波器的模拟，以便利用它们的一些有趣特性。

无源滤波器

集中元件滤波器

集中元件滤波器基于以下元件的频率特性

• 电阻，R
• 电容，C
• 电感，L

它们的特性由下式给出

$U=R\cdot I$

$U={\frac {1}{sC}}\cdot I$

$U=sL\cdot I$

梯形滤波器

下图显示了一个四阶全极点低通梯形滤波器

集中元件梯形滤波器四阶

电路的整体外观解释了这个名字。

在图中，源电阻和负载电阻是相同的。这对应于源到负载的最佳能量传输情况。在直流情况下，电感充当短路，电容充当开路。因此，输出幅度将是输入幅度的一半。

双端梯形滤波器具有 优异的通带灵敏度特性 。换句话说，L 或 C 元件值的给定变化会导致滤波器传递函数的相对变化小得多。因此，梯形滤波器已被广泛用作模拟有源滤波器和数字滤波器的模型。

分布元件滤波器

一个 分布元件滤波器 是一种电子滤波器，其中电容、电感和电阻（电路的元件）不是像传统滤波器那样集中在离散（集中）元件中。在高频，在微波区域，印刷电路板上的条带充当阻抗，精心设计它们可以实现滤波器功能。

有源滤波器

有源滤波器是使用放大器件（如运算放大器）的模拟滤波器。它们允许使用电阻和电容实现滤波器功能，使设计人员不必使用电感。

典型滤波器

实现有源滤波器的首次尝试是设计一个电路来实现传递函数，其中 R 和 C 元件值组合对应于传递函数的分子和分母系数：典型滤波器。然而，这种电路显示出对元件值的敏感性非常高：R 或 C 元件值的微小变化会对传递函数产生很大的影响。

出于这个原因，有源滤波器的设计已从典型滤波器转向其他结构，例如二阶段串联或交错滤波器。

二阶段串联

一个二阶段，通常称为双二阶，实现一个二阶传递函数。滤波器的传递函数可以分解为传递函数的乘积，每个传递函数与一对极点和可能的一对零点相关联。

具有相同数量复共轭零点 $z_{i}$ 和 $z_{i}^{*}$，以及极点 $p_{i}$ 和 $p_{i}^{*}$，以及增益 $k$ 的系统的传递函数为

$H(s)=k\cdot \prod _{i=1}^{N/2}{\frac {(s-z_{i})(s-z_{i}^{*})}{(s-p_{i})(s-p_{i}^{*})}}$

这是切比雪夫二型和椭圆 滤波器函数 的情况。

写

$D_{i}(s)=(s-p_{i})(s-p_{i}^{*})=s^{2}-2Re(p_{i})s+abs(p_{i})^{2}=s^{2}+a_{1i}s+a_{0i}$

表明 $s$ 的分母多项式函数具有实系数。分子也可以这样说。由此，传递函数可以改写为

$H(s)=k\cdot \prod _{i=1}^{N/2}{\frac {s^{2}+b_{1i}s+b_{0i}}{s^{2}+a_{1i}s+a_{0i}}}$

如果传递函数的阶数为奇数，则需要在链中添加一个一阶部分。该部分与实极点 $p_{r}$ 和实零点 $z_{r}$ 相关联，如果存在的话。传递函数变为

$H(s)=k\cdot {\frac {s-z_{r}}{s-p_{r}}}\cdot \prod _{i=1}^{{N-1}/2}{\frac {s^{2}+b_{1i}s+b_{0i}}{s^{2}+a_{1i}s+a_{0i}}}$

全极点偶数阶传递函数的形式为

$H(s)=k\cdot \prod _{i=1}^{N/2}{\frac {1}{(s-p_{i})(s-p_{i}^{*})}}=k\cdot \prod _{i=1}^{N/2}{\frac {1}{s^{2}+a_{1i}s+a_{0i}}}$

这种情况适用于巴特沃斯、切比雪夫一型和贝塞尔 滤波器函数。

一个全极点奇数阶传递函数的形式为

$H(s)=k\cdot {\frac {1}{s-p_{r}}}\cdot \prod _{i=1}^{{N-1}/2}{\frac {1}{s^{2}+a_{1i}s+a_{0i}}}$

状态变量滤波器

状态变量滤波器 具有两个积分器的拓扑结构，其输出对应于与传递函数相关的状态空间变量。

以下电路是由 Kerwin、Huelsman 和 Newcomb 提出的

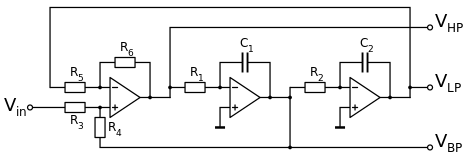
以下电路被称为 Tow-Thomas 电路

通过 Kerwin-Huelsman-Newcomb 和 Tow-Thomas，都可以通过对所有运算放大器输出进行加权求和来获得更通用的传递函数。

某些二阶 规范结构 直接使用传递函数的系数作为放大器增益。

萨伦-基电路

萨伦-基 拓扑结构使用运算放大器驱动输出，并使用 RC 元件设置传递函数。由于运算放大器的驱动能力，萨伦-基电路很容易级联形成更高阶的滤波器。

以下电路显示了一个萨伦-基低通滤波器电路

跳跃滤波器

滤波器结构

跳跃滤波器 基于对 无源梯形滤波器 的模拟。这种选择的动机是继承原始电路优异的通带灵敏度特性。

以以下 4 阶全极点低通梯形滤波器为例，

集中元件梯形滤波器四阶

可以写出以下方程

${\begin{cases}sC_{1}\cdot U_{1}={\frac {1}{R}}\cdot (U_{in}-U_{1})-I_{2}\\sL_{2}\cdot I_{2}=U_{1}-U_{3}\\sC_{3}\cdot U_{3}=I_{2}-I_{4}\\sL_{4}\cdot I_{4}=U_{3}-R\cdot I_{4}\\U_{out}=R\cdot I_{4}\end{cases}}$

重写这些方程得到

${\begin{cases}U_{1}={\frac {1}{sRC_{1}}}(U_{in}-U_{1}-RI_{2})\\RI_{2}={\frac {R}{sL_{2}}}(U_{1}-U_{3})\\U_{3}={\frac {1}{sRC_{3}}}(RI_{2}-RI_{4})\\RI_{4}={\frac {R}{sL_{4}}}(U_{3}-RI_{4})\\U_{out}=RI_{4}\end{cases}}$

这个新的方程组表明，该滤波器可以用 4 个积分器链实现，

• 状态变量 形如 $w_{i}=U_{i}$ 或 $w_{i}=RI_{i}$
• 时间常数 形如 $t_{i}=RC_{i}$ 或 $t_{i}={\frac {L_{i}}{R}}$

得到的电路是一个积分器链，每个积分器的输出都被反馈到前一个积分器的输入。因此称为跳跃。

传递函数

描述滤波器的方程组可以使用状态空间表示重写为

${\begin{array}{ccrcccccc}s\cdot {\begin{bmatrix}U_{1}\\RI_{2}\\U_{3}\\RI_{4}\end{bmatrix}}&=&{\begin{bmatrix}-{\frac {1}{t_{1}}}&-{\frac {1}{t_{1}}}&0&0\\{\frac {1}{t_{2}}}&0&-{\frac {1}{t_{2}}}&0\\0&{\frac {1}{t_{3}}}&0&-{\frac {1}{t_{3}}}\\0&0&{\frac {1}{t_{4}}}&-{\frac {1}{t_{4}}}\end{bmatrix}}&\cdot &{\begin{bmatrix}U_{1}\\RI_{2}\\U_{3}\\RI_{4}\end{bmatrix}}&+&{\begin{bmatrix}{\frac {1}{t_{1}}}\\0\\0\\0\end{bmatrix}}&\cdot &U_{in}\\U_{out}&=&{\begin{bmatrix}0&0&0&1\end{bmatrix}}&\cdot &{\begin{bmatrix}U_{1}\\RI_{2}\\U_{3}\\RI_{4}\end{bmatrix}}&+&{\begin{bmatrix}0\end{bmatrix}}&\cdot &U_{in}\end{array}}$

从这个方程组中，我们可以写出 A、B、C、D 矩阵为

$A={\begin{bmatrix}-{\frac {1}{t_{1}}}&-{\frac {1}{t_{1}}}&0&0\\{\frac {1}{t_{2}}}&0&-{\frac {1}{t_{2}}}&0\\0&{\frac {1}{t_{3}}}&0&-{\frac {1}{t_{3}}}\\0&0&{\frac {1}{t_{4}}}&-{\frac {1}{t_{4}}}\end{bmatrix}}$

$B={\begin{bmatrix}{\frac {1}{t_{1}}}\\0\\0\\0\end{bmatrix}}$

$C={\begin{bmatrix}0&0&0&1\end{bmatrix}}$

$D={\begin{bmatrix}0\end{bmatrix}}$

通过这种表示方式，信号处理工具例如Octave 或Matlab 可以用来绘制滤波器的频率响应或检查其零点和极点。

开关电容滤波器

开关电容滤波器是模拟采样器件。对电容器进行充放电可以产生类似于电阻的阻抗。这样，模拟有源滤波器的RC时间常数就变成了两个电容之比的比例因子。这种类型的电路对于集成电路设计非常有用，因为在同一个硅芯片的不同区域，R和C元件的值可能会有很大差异，而两个电容之比在同一个区域内的偏差却非常小。