信号与系统/伯德图

信号与系统

频率响应图

频率响应是频率响应的复函数，其变量为角频率 $\omega =2\pi \cdot f$

H(j\omega )={\frac {Y(j\omega )}{X(j\omega )}}

或变量 $s=i\omega$

H(s)={\frac {Y(s)}{X(s)}}

这些函数给出了线性时不变系统的输入和输出之间的关系。频率响应以两个多项式的比率的形式给出

H(s)=k\cdot {\frac {b_{M}s^{M}+\dots +b_{2}s^{2}+b_{1}s+b_{0}}{a_{N}s^{N}+\dots +a_{2}s^{2}+a_{1}s+a_{0}}}

分子为零的点称为传递函数的零点。分母为零的点称为传递函数的极点。零点和极点都是实数或复共轭。

只有复共轭零点 $z_{i}$ 和 $z_{i}^{*}$ ，以及极点 $p_{i}$ 和 $p_{i}^{*}$ 的系统的传递函数可以写成

H(s)=k\cdot {\frac {\prod _{i=1}^{M/2}{(s-z_{i})(s-z_{i}^{*})}}{\prod _{i=1}^{N/2}{(s-p_{i})(s-p_{i}^{*})}}}

如果存在实数零点 $z_{r}$ 和实数极点 $p_{r}$ ，则传递函数变为

H(s)=k\cdot {\frac {s-z_{r}}{s-p_{r}}}\cdot {\frac {\prod _{i=1}^{(M-1)/2}{(s-z_{i})(s-z_{i}^{*})}}{\prod _{i=1}^{(N-1)/2}{(s-p_{i})(s-p_{i}^{*})}}}

频率响应通常表示为两个图的组合：幅频响应和相频响应。

波德图以对数尺度表示频率和幅度，分别表示幅频响应和相频响应。

频率轴显示 $\log _{10}(f)$ 。两个频率之间比率为10的跨度称为十倍频程。

幅度轴显示 $20\cdot \log _{10}(|H(j\omega )|)$ ，这是以分贝为单位的幅度。

这种表示方式的优点在于，实零点、实极点、共轭零点对和共轭极点对的影响在表示中叠加。

示例

此示例显示了三阶归一化巴特沃斯滤波器的波德图。

三阶巴特沃斯滤波器有3个极点：一个实极点和两个复共轭极点。所有极点在圆的左侧均匀分布。

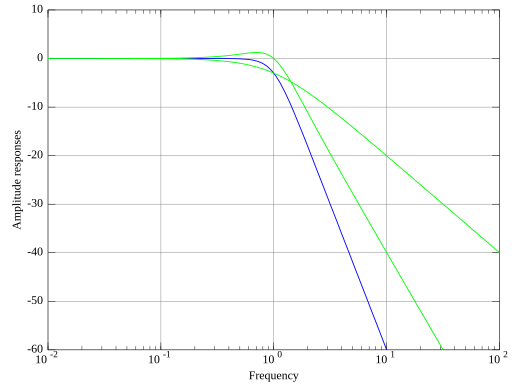
下面的幅度图以绿色显示

滤波器响应以蓝色显示。它以 -60 dB/十倍频程的斜率衰减。

在波德图中，总的幅频响应（蓝色）可以绘制为所有实极点或共轭极点对（绿色）的幅频响应之和。

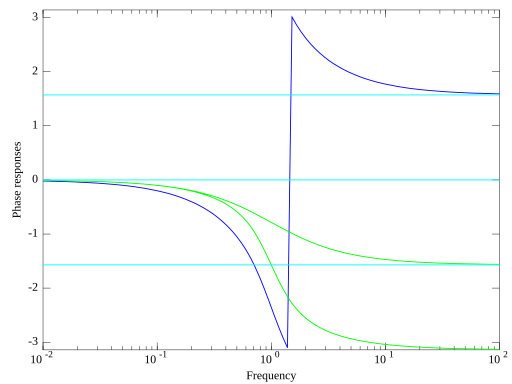
下面的相位图以绿色显示

滤波器相位响应以蓝色显示。它偏移 $3\pi /2$ 。

在波德图中，总的相频响应（蓝色）可以绘制为所有实极点或共轭极点对（绿色）的相频响应之和。

因此，了解每个独立的实极点和复共轭极点对的响应，就可以绘制总的幅频响应和相频响应。