狭义相对论/相对性原理

相对性原理

伽利略·伽利雷

相对性原理探讨了在不同地点进行观察之间的关系。这个问题自古以来就是一个艰难的理论挑战，涉及物理问题，例如物体的速度如何组合以及影响如何在运动物体之间传递。

解决这个问题最有效的方法之一是研究观察者速度对观察的影响。这个问题曾被古典哲学家们解决过，但伽利略的工作取得了真正的突破。 伽利略 (1632) 在他的 关于两大世界体系的对话 中，考虑了船内的人所做的运动观察，他们看不到船外

"让船以你喜欢的任何速度前进，只要运动是均匀的，而不是这样那样地波动。你将发现所有提到的效应没有发生丝毫变化，你也不会从其中任何一个效应中判断出船是在运动还是静止的。"

根据伽利略，如果船平稳移动，那么船内的人就无法判断他们是否在移动。如果伽利略在移动的船上的人正在吃晚饭，他们会看到他们的豌豆从叉子上直直地掉到他们的盘子里，就像他们在陆地上家里一样。豌豆随着人们一起移动，对就餐者来说不会看起来是斜着掉落的。这意味着豌豆保持匀速运动状态，除非有人拦截它们或以其他方式作用于它们。这也意味着人们在船上进行的简单实验在船上或在家里会得到相同的结果。这个概念导致了“伽利略相对论”，它认为物体除非受到作用，否则将保持运动状态，并且物理定律与实验室的速度无关。

这个简单的想法挑战了之前亚里士多德的观点。 亚里士多德 在他的《物理学》中 认为物体必须要么被移动要么处于静止状态。根据亚里士多德的说法，基于对“虚空”可能性复杂而有趣的论证，物体在没有东西推动的情况下不能保持运动状态。因此，亚里士多德认为物体会在空旷的空间中完全停止。如果亚里士多德是正确的，那么你在移动的船上吃饭时掉落的豌豆会落在你的腿上，而不是直直地掉到你的盘子上。亚里士多德的观点被所有人接受，因此伽利略的新提议是异乎寻常的，并且因为它几乎是正确的，所以它成为了物理学的基础。

伽利略相对论包含两个重要原则：首先，不可能确定谁实际上处于静止状态；其次，物体除非受到作用，否则将保持匀速运动状态。第二个原则被称为伽利略惯性定律或牛顿第一运动定律。

狭义相对论

直到 19 世纪，伽利略相对论似乎认为所有观察者都是等价的，无论他们移动的速度有多快。如果你在北极向上抛一个球，它会直直地落下来，这在赤道上也会发生，尽管赤道比极点快近一千英里。伽利略速度是可加的，因此当你在赤道向上抛球时，球会以一千英里的速度继续运动，并且会继续以这个速度运动，直到它受到外部作用力的作用。

这个简单的方案在 1865 年被詹姆斯·克莱克·麦克斯韦发现的描述光等电磁波传播的方程所质疑。他的方程表明光速取决于被认为是充满所有空间的物理介质或“以太”的简单特性的常数。如果是这种情况，那么根据伽利略相对论，应该可以将你自己的速度加到入射光的速度上，因此，如果你以光速的一半速度旅行，那么任何朝你射来的光都会被观察到在以太中以 1.5 倍的光速旅行。同样，任何从你身后射来的光都会以以太中光速的 0.5 倍的速度撞击你。光本身始终以以太中的相同速度传播，因此如果你在高速行驶时用电筒照射光，光会进入以太并减慢到它的正常速度。这将破坏伽利略的相对论，因为你只需要做的一件事就是测量不同方向的光速来发现你是在移动的船上还是在陆地上。光在你通过以太的运动方向上会变慢，而在相反方向上会变快。

如果麦克斯韦方程是有效的，并且简单的经典速度加法适用，那么应该存在一个优先参考系，即静止以太的框架。优先参考系将被认为是所有速度测量都可以参考的真实零点。

狭义相对论通过保持麦克斯韦方程是正确的，但经典速度加法是错误的，从而恢复了物理学中的相对性原理：不存在优先参考系。狭义相对论恢复了以下解释：在所有惯性参考系中，相同的物理现象正在发生，并且不存在允许观察者确定速度零点的现象。 爱因斯坦 通过提出物理定律与观察者的速度无关，从而保留了相对性原理。根据爱因斯坦的说法，无论你是在伽利略船的货舱里，还是在以光速很大一部分速度运行的宇宙飞船的货舱里，物理定律都将是相同的。

爱因斯坦的想法与伽利略的想法具有相同的哲学，两人都相信物理定律不会受到匀速运动的影响。在伽利略和爱因斯坦之间的岁月里，人们认为正是速度简单地相互加成的方式保留了物理定律，但爱因斯坦调整了这个简单概念，以允许麦克斯韦方程成立。

参考系、事件和变换

在进一步分析相对运动之前，需要更仔细地定义参考系、事件和变换的概念。

物理观察者被认为被参考系包围，参考系是一组坐标轴，用它可以指定位置或运动，或者用它可以数学地描述物理定律。

事件是指独立于可能用于描述它的参考系而发生的事情。打开一盏灯或两个物体的碰撞将构成一个事件。

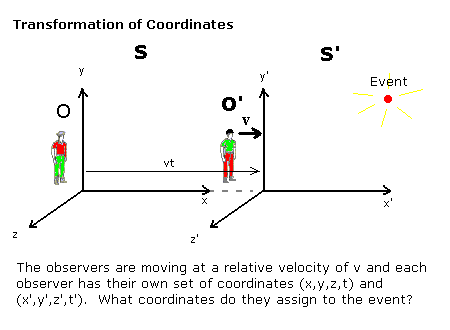
假设有一个小事件，例如打开一盏灯，它在一个参考系中的坐标为 $x,y,z,t$。另一个观察者在另一个参考系中以速度 $v$ 相对于第一个参考系沿着 $x$ 轴移动，会将事件分配给事件什么坐标呢？这个问题在下面进行了说明

我们正在寻找的是事件 $x^{'},y^{'},z^{'},t^{'}$ 的第二个观察者坐标与事件 $x,y,z,t$ 的第一个观察者坐标之间的关系。坐标指的是每个观察者测量的事件的位置和时间，为了简单起见，观察者被安排在 $t=0$ 时重合。

根据伽利略相对论

$x^{'}$ $=x-vt$

$y^{'}$ = $y$

$z^{'}$ = $z$

$t^{'}$ = $t$

这组方程被称为伽利略坐标变换或伽利略变换。

这些方程表明，在一个参考系中事件的位置如何与另一个参考系中事件的位置相关。但如果事件是正在移动的东西，会发生什么呢？速度如何从一个框架转换到另一个框架呢？

速度的计算依赖于牛顿公式：$v=dx/dt$。使用牛顿物理学来计算速度和其他物理变量，导致伽利略相对论在得出超出简单坐标变化的结论时被称为牛顿相对论。根据伽利略相对论，三个空间方向上的速度变换为

$\mathbf {u_{x}^{'}=u_{x}-v}$

$\mathbf {u_{y}^{'}=u_{y}}$

其中 $\mathbf {u_{x}^{'},u_{y}^{'},u_{z}^{'}}$ 是第二个观察者记录的运动物体在空间三个方向上的速度，而 $\mathbf {u_{x},u_{y},u_{z}}$ 是第一个观察者记录的速度，而 $\mathbf {v}$ 是两个观察者的相对速度。 $\mathbf {v}$ 前面的减号表示运动物体正在远离两个观察者。

这个结果被称为经典速度加法定理，它总结了两个伽利略参考系之间的速度变换。这意味着，必须根据抛射体源头和目标的速度来确定抛射体的速度。例如，如果一个水手从伽利略的船上以 10 公里/小时的速度向岸边扔一块石头，而伽利略的船以 5 公里/小时的速度向岸边移动，那么石头击中岸边时将以 15 公里/小时的速度移动。

在牛顿相对论中，空间几何被认为是欧几里得的，所有观察者的时间测量都被认为是相同的。

经典速度加法定理的推导如下。
如果伽利略变换对时间进行微分

$x^{'}=x-vt$

所以

$dx^{'}/dt=dx/dt-v$

但在伽利略相对论中，$t^{'}=t$，所以 $dx^{'}/dt^{'}=dx^{'}/dt$ 因此

$dx^{'}/dt^{'}=dx/dt-v$

$dy^{'}/dt^{'}=dy/dt$

$dz^{'}/dt^{'}=dz/dt$

如果我们写 $u_{x}^{'}=dx^{'}/dt^{'}$ 等，那么

$u_{x}^{'}=u_{x}-v$

$u_{y}^{'}=u_{y}$

$u_{z}^{'}=u_{z}$

狭义相对论的假设

上一节描述了从一个参考系到另一个参考系的转换，使用的是伽利略时代提出的简单速度叠加。这些转换与伽利略的主要假设一致，即物理定律对所有惯性观察者都是相同的，因此没有人能够分辨谁是静止的。以太理论对伽利略的假设提出了质疑，因为以太是静止的，观察者可以通过测量光在运动方向上的速度来判断自己是否静止。爱因斯坦保留了伽利略的基本假设，即物理定律在所有惯性参考系中都是相同的。但为了做到这一点，他必须引入一个新的假设，即光速对所有观察者都是相同的。这些假设列举如下

1. 第一个假设：相对性原理

正式表述：物理定律在所有惯性参考系中都是相同的。

非正式表述：任何物理理论对每个惯性观察者来说，在数学上都应该是一样的。在一个围绕太阳和银河系运行的宇宙飞船或星球上的物理实验室进行的实验将给出相同的结果，无论实验室的速度有多快。

2. 第二个假设：光速不变性

正式表述：在所有惯性参考系中，自由空间中的光速都是一个常数。

非正式表述：真空中光速，通常用c表示，对所有惯性观察者来说都是相同的；在所有方向都是相同的；并且不依赖于发射光的物体速度。

使用这些假设，爱因斯坦能够计算出事件的观测结果如何取决于观察者的相对速度。然后，他能够构建一个物理理论，并由此产生了一些预言，比如质量和能量的等价性以及早期的量子理论。

爱因斯坦对相对论公理的表述被称为电动力学方法。在大多数高级教科书中，它已被时空方法所取代，在时空方法中，物理定律本身是由于时空中的对称性造成的，而光速的恒定性则是时空存在的自然结果。然而，爱因斯坦的方法同样有效，它代表了一次演绎推理的壮举；它为现代处理该主题提供了必要的洞察力。

爱因斯坦的相对论——电动力学方法

爱因斯坦问，如果两个观察者都发现光速是恒定的，那么他们测量的长度和时间可能需要如何变化？他观察了两个观察者用来计算光速的公式，$(x=ct)$和$(x^{'}=ct^{'})$，并询问需要引入哪些常数才能保持光速的测量值保持相同，即使观察者的相对运动意味着$x^{'}$轴不断前进。他的工作在附录中详细展示。这个计算的结果是洛伦兹变换方程

$x'=\gamma (x-vt)\,$

$y'=y\,$

$z'=z\,$

$t'=\gamma (t-{\frac {vx}{c^{2}}})\,$

其中常数 $\gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}$。这些方程适用于任何两个相对运动的观察者，但请注意括号内的符号会根据速度的方向而改变 - 请参见附录。

洛伦兹变换相当于伽利略变换，只是增加了每个人都测量到相同的光速的假设，无论他们运动的速度有多快。光速是距离与时间的比率（即：米每秒），因此对于每个人来说，测量到的光速值都相同，测量杆的长度、光源和接收器之间的空间长度以及时钟的滴答次数必须在观察者之间动态地有所不同。只要长度和时间间隔随两个观察者的相对速度 (v) 变化，如洛伦兹变换所描述的那样，观察者都可以将光速计算为光线传播的距离与传播该距离所花费的时间之比，并得到相同的值。

爱因斯坦的方法是“电动力学”的，因为它假设，根据麦克斯韦方程组，光以恒定速度传播。如上所述，普遍恒定速度的概念很奇怪，因为速度是距离与时间的比率。洛伦兹变换方程是否掩盖了关于空间和时间的更深层的真相？爱因斯坦本人 对洛伦兹变换方程是如何实际描述空间和时间本身的性质给出了最清晰的描述之一。他的总体推理如下。

如果将这些方程组合起来，它们满足以下关系

(1) $x^{'2}-c^{2}t^{'2}=x^{2}-c^{2}t^{2}\,$

爱因斯坦 (1920) 描述了如何将其扩展以描述在空间中任何方向上的运动

(2) $x^{'2}+y^{'2}+z^{'2}-c^{2}t^{'2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}\,$

方程 (2) 是关于宇宙中长度和时间关系的几何公理。它表明存在一个常数 s，使得

$s^{2}=x^{'2}+y^{'2}+z^{'2}-c^{2}t^{'2}\,$

$s^{2}=x^{2}+y^{2}+z^{2}-c^{2}t^{2}\,$

这个方程被闵可夫斯基认为是毕达哥拉斯定理（即 $s^{2}=x^{2}+y^{2}$）的扩展，这种扩展在 20 世纪初的数学中是众所周知的。洛伦兹变换告诉我们，宇宙是一个四维时空，因此不需要任何“以太”。（参见爱因斯坦 1920，附录，了解爱因斯坦关于洛伦兹变换如何表明一个四维宇宙的讨论，但请注意，“虚时间”现在已被“度量张量”的使用所取代）。

爱因斯坦的分析表明，两个相对运动的观察者的 x 轴和时间轴不会重叠。将一个观察者的时间与另一个观察者的时间联系起来的方程表明，这种关系随 x 轴上的距离而变化，即

$t'=\gamma (t-{\frac {vx}{c^{2}}})\,$

这意味着“参考系”的整个概念需要重新审视，以允许轴不再重叠的方式。

惯性参考系

洛伦兹变换对时间的变换涉及一个分量 $(vx/c^{2})$，这导致沿相对移动的观察者的 x 轴的时间测量值不同。这意味着不再适用简单地涉及三个空间维度且所有观察者共享相同的时间的参考系的概念。要比较观察者之间的测量值，必须将“参考系”的概念扩展到包括观察者的时钟。

惯性参考系是一个概念上的三维格架，由相互垂直的测量杆组成，在每个点上都有相互同步的时钟（有关完整定义，请参见下文）。定义为属于或连接到惯性参考系的物体，是一个不干扰时钟同步并保持在参考系内恒定空间位置的物体。与运动的非旋转物体相连或附着的惯性参考系被称为该物体的惯性静止系。对于特定物体，惯性参考系是该物体的静止系，当由相对运动的观察者观察时，它会随着物体一起运动。

这种类型的参考系被称为“惯性”参考系，因为，如将在本书后面看到的那样，每个根据牛顿惯性定律（没有旋转、引力场或作用力）共同运动的物体系统都有一个共同的静止系，其时钟同步和杆长度与其他相对运动的静止系中的时钟和杆不同。

关于“惯性参考系”有很多其他的定义，但大多数定义，比如“惯性参考系是牛顿第一定律有效的参考系”，都没有提供关于坐标如何排列和/或代表从更基本定义推导出的必要细节。

Blandford 和 Thorne（2004）给出的以下定义是对工作物理学家所指的惯性参考系的相当完整的总结。

“惯性参考系是一个（概念上的）三维的测量杆和时钟网络，具有以下性质：（i）该网络在时空中自由移动（即不受任何力的作用），并且连接到陀螺仪上，因此它不会相对于遥远的宇宙天体旋转。 （ii）测量杆形成一个正交网络，并且刻在它们上面的长度间隔在与例如由某种类型的标准原子或分子发射的光的波长相比时是均匀的；因此，杆形成了一个正交的笛卡尔坐标系，其中坐标x沿着一个轴测量，y沿着另一个轴测量，z沿着第三个轴测量。（iii）时钟密集地分布在整个网络中，因此，理想情况下，在每个网络点都有一个单独的时钟。 （iv）与例如某种类型的标准原子或分子发射的光的周期相比，这些时钟的滴答声是均匀的；即它们是理想的时钟。 （v）时钟通过爱因斯坦同步过程同步：如果一个时钟发射的光脉冲从连接到另一个时钟的镜子反射回来，然后返回，则反弹时间$t_{b}$由进行反弹的时钟测量，是发射和接收时间的一半，由发射和接收时钟测量：$t_{b}=1/2(t_{e}+t_{r})$。¹

¹有关理想时钟和理想测量杆性质的更深入讨论，请参阅例如 Misner、Thorne 和 Wheeler（1973）的第 23-29 页和 395-399 页。

狭义相对论表明，相对于彼此运动的物体的惯性静止系不会重叠。每个观察者都看到另一个运动观察者的惯性参考系发生了扭曲。这一发现是狭义相对论的本质，意味着在运动的观察者之间，坐标和其他测量的转换非常复杂。将在下面深入讨论。