指数
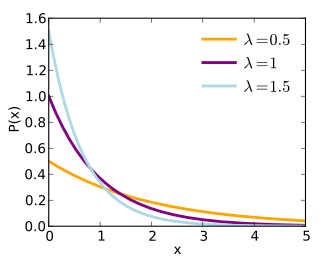
概率密度函数
|
累积分布函数

|
| 参数 |
λ > 0 速率,或 尺度 的倒数 |
| 支撑
|
x ∈ [0, ∞)
|
| PDF
|
λ e−λx
|
| CDF
|
1 − e−λx
|
| 平均值
|
λ−1 |
| 中位数
|
λ−1 ln 2
|
| 众数
|
0
|
| 方差
|
λ−2 |
| 偏度
|
2
|
| 超额峰度
|
6
|
| 熵
|
1 − ln(λ)
|
| MGF
|

|
| CF
|

|
指数分布是指一种统计分布,用于模拟独立事件之间的间隔时间,这些事件以恒定的平均速率λ发生。这个分布的一些例子是
- 一辆车经过上一辆车之后经过的距离。
- 放射性粒子衰变的速率。
对于随机变量X,它的概率分布函数是

而累积分布函数是

指数分布记为  ,其中m是给定时间段内事件的平均数量。所以如果m=3每分钟,即每分钟有3个事件,那么λ=1/3,即平均每20秒发生一次事件。
,其中m是给定时间段内事件的平均数量。所以如果m=3每分钟,即每分钟有3个事件,那么λ=1/3,即平均每20秒发生一次事件。
我们如下推导出平均值。
![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c925eb7f3d99af3083ee5838c3bec6f3838997a)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de21e0e435a11373f8f68aa9365a100fd28434b7)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }(-x)(-\lambda e^{-\lambda x})dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e2936bccbe650f7919d6dfeb9db772d222f370)
我们将使用 分部积分法,其中 u=−x 和 v=e−λx。我们可以看到 du=-1 和 dv=−λe−λx。
![{\displaystyle \operatorname {E} [X]=\left[-x\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-1)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0a325796212c52d7cc34c2e57e5e0a5869121f)
![{\displaystyle \operatorname {E} [X]=[0-0]+\left[{-1 \over \lambda }(e^{-\lambda x})\right]_{0}^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfc71b113a0864019d9801c659d3ac3294525e2)
![{\displaystyle \operatorname {E} [X]=\left[0-{-1 \over \lambda }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc46e6600d22129f1f8916bd6bcfa332679719e)
![{\displaystyle \operatorname {E} [X]={1 \over \lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf488e5f107cc237b5235226664cf3b1d5c02bcd)
我们使用以下公式来计算方差。
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5a922df13bdee788c0f06474fe002a42c25d8a)


我们将使用分部积分法,其中  和
和  。由此得到
。由此得到  和
和  .
.
![{\displaystyle \operatorname {Var} (X)=\left\{\left[-x^{2}\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-2x)dx\right\}-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa497aeeb4e8301234482593735ec9726a74a95)
![{\displaystyle \operatorname {Var} (X)=[0-0]+{2 \over \lambda }\int _{0}^{\infty }x\lambda e^{-\lambda x}dx-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620c93fc59bb00faabfa622a4b600f2a0dc8ac42)
我们可以看到,这个积分就是![{\displaystyle \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93) ,我们已经在上面解决了。
,我们已经在上面解决了。










![{\displaystyle \operatorname {E} [X]=\int _{-\infty }^{\infty }x\cdot f(x)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c925eb7f3d99af3083ee5838c3bec6f3838997a)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }x\lambda e^{-\lambda x}dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de21e0e435a11373f8f68aa9365a100fd28434b7)
![{\displaystyle \operatorname {E} [X]=\int _{0}^{\infty }(-x)(-\lambda e^{-\lambda x})dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22e2936bccbe650f7919d6dfeb9db772d222f370)
![{\displaystyle \operatorname {E} [X]=\left[-x\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-1)dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0a325796212c52d7cc34c2e57e5e0a5869121f)
![{\displaystyle \operatorname {E} [X]=[0-0]+\left[{-1 \over \lambda }(e^{-\lambda x})\right]_{0}^{\infty }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcfc71b113a0864019d9801c659d3ac3294525e2)
![{\displaystyle \operatorname {E} [X]=\left[0-{-1 \over \lambda }\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcc46e6600d22129f1f8916bd6bcfa332679719e)
![{\displaystyle \operatorname {E} [X]={1 \over \lambda }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf488e5f107cc237b5235226664cf3b1d5c02bcd)
![{\displaystyle \operatorname {Var} (X)=\operatorname {E} [X^{2}]-(\operatorname {E} [X])^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd5a922df13bdee788c0f06474fe002a42c25d8a)






![{\displaystyle \operatorname {Var} (X)=\left\{\left[-x^{2}\cdot e^{-\lambda x}\right]_{0}^{\infty }-\int _{0}^{\infty }(e^{-\lambda x})(-2x)dx\right\}-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6aa497aeeb4e8301234482593735ec9726a74a95)
![{\displaystyle \operatorname {Var} (X)=[0-0]+{2 \over \lambda }\int _{0}^{\infty }x\lambda e^{-\lambda x}dx-{1 \over \lambda ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620c93fc59bb00faabfa622a4b600f2a0dc8ac42)
![{\displaystyle \operatorname {E} [X]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44dd294aa33c0865f58e2b1bdaf44ebe911dbf93)

