卡诺循环描述了热量转化为能量的热力学循环。该循环遵循四个可逆步骤:(1)等温膨胀,(2)绝热膨胀,(3)等温压缩和(4)绝热压缩。由于循环的两个特性,即可逆性和在最热储层和最冷储层之间进行最大可能的热量传递,因此可以实现正净功。这在下图和表格中显示。
 卡诺循环及其储层的图片
卡诺循环及其储层的图片
 卡诺循环的P-T图
卡诺循环的P-T图
根据该图,热量从热储层T(1)转移到发动机,由Q(1)表示。Q(1)和Q(2)的符号相反,因为热机的效率是进入系统的总热量减去离开系统的总热量。
对于右侧的图,热机的P-T图显示,总功是顶部曲线面积和底部曲线面积之间的差。它还表明,根据热力学第二定律,热机的热量传递效率不可能达到100%。以下公式显示了热机效率,该公式用于推导出自发性的第二定律。

也可以用两种其他方式表示
 或
或 
卡诺循环的P-T图可以根据下表分为四个步骤。从步骤1到步骤2,存在等温膨胀,这意味着内能 等于零。这使得q = -w,可以计算第一次等温膨胀的工作量。随后,存在绝热膨胀,其中热量传递q等于零,表明
等于零。这使得q = -w,可以计算第一次等温膨胀的工作量。随后,存在绝热膨胀,其中热量传递q等于零,表明 ,而从步骤2到步骤3再到步骤4,分别存在等温膨胀和绝热膨胀。方程式显示在表格中。
,而从步骤2到步骤3再到步骤4,分别存在等温膨胀和绝热膨胀。方程式显示在表格中。
 卡诺循环表
卡诺循环表
来源:Castellan,Gilbert W. 物理化学。第3版。门洛帕克:Addison-Wesley P C,1983。
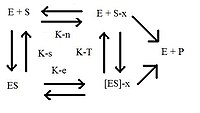 酶及其底物的热力学循环。添加的后缀-x表示该分子处于其过渡态
酶及其底物的热力学循环。添加的后缀-x表示该分子处于其过渡态
根据过渡态理论,酶是灵活的蛋白质分子,可以催化经历初始构象和最终构象之间过渡态阶段的分子。底物的过渡态或“半椅”构象比基态或最终态与酶的反应性更高(有关更多详细信息,请参阅过渡态)。这种最新的理论被称为过渡态稳定化。使用X射线晶体学和诱变方法或酶的氨基酸的改变,有助于获得更多关于过渡态稳定化的知识。
该理论基于两个假设,即反应受到动态瓶颈的限制,并且该反应处于平衡状态。该理论的一般公式为

其中k是反应速率常数, 是传递系数,
是传递系数, 是频率,以及
是频率,以及
 是平衡常数。常数
是平衡常数。常数 只是影响反应速率的无关因素的校正因子。
只是影响反应速率的无关因素的校正因子。
使用所示的图,比较酶和酶过渡态的两个反应速率。

其中下标 e 和 n 分别代表酶促和非酶促活性。由于  等同于最简单形式的催化速率常数
等同于最简单形式的催化速率常数  ,该方程式可以用解离常数
,该方程式可以用解离常数  和过渡态常数
和过渡态常数  表示为
表示为

由于酶促反应速率很大,因此比例  通常为
通常为  到
到  。比例
。比例  可以从方程中去掉,因为它不太可能使酶与非酶速率反应的偏差很大。因此,最终的方程式推导为
可以从方程中去掉,因为它不太可能使酶与非酶速率反应的偏差很大。因此,最终的方程式推导为

表明过渡态的结合能力大于基态底物。
Kraut, Joseph. “酶是如何起作用的?” 研究文章。加州大学圣地亚哥分校教授。发表于 1988 年 10 月。
























