我们将计算当没有平衡吸引力(如原子氢中原子核和电子之间的吸引力)时,位置概率分布的模糊度随着相应动量的模糊度增加而增加的速率。
由于易于处理,我们选择高斯函数

它具有钟形曲线图。它定义了位置概率分布

如果我们将此分布归一化,使得  那么
那么  并且
并且

我们还有

 的傅里叶变换是
的傅里叶变换是 
- 它定义了动量概率分布

- 并且

与  相关的粒子的位置和动量的模糊度,因此是 "不确定性"关系 允许的最小值:
相关的粒子的位置和动量的模糊度,因此是 "不确定性"关系 允许的最小值:
现在回想一下

其中  它的傅里叶变换为
它的傅里叶变换为
![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
这定义了位置概率分布
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)
与  的比较表明
的比较表明  因此,
因此,
![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)
以下图表说明了,与一个质量相当于  分子或花生大小的物体相比,一个电子质量的粒子的模糊度增长得有多快。这里我们看到,为什么宏观物体的“一旦清晰,永远清晰”的立场是成立的,但事实并非如此,因为它并不是唯一的原因。
分子或花生大小的物体相比,一个电子质量的粒子的模糊度增长得有多快。这里我们看到,为什么宏观物体的“一旦清晰,永远清晰”的立场是成立的,但事实并非如此,因为它并不是唯一的原因。
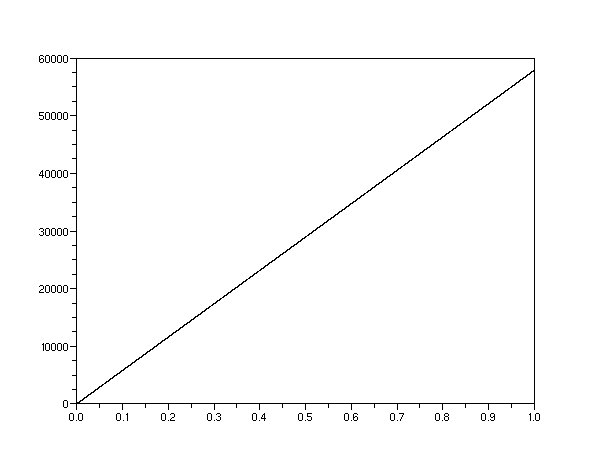
上图:一个电子, 纳米。在一秒钟内,
纳米。在一秒钟内, 增加到近 60 公里。
增加到近 60 公里。
下图:一个电子, 厘米。
厘米。  在一秒钟内只增长了 16%。
在一秒钟内只增长了 16%。

接下来,一个 分子,
分子, 纳米。在一秒钟内,
纳米。在一秒钟内, 增加到 4.4 厘米。
增加到 4.4 厘米。

最后,一颗花生 (2.8 克), 纳米。
纳米。 需要宇宙的当前年龄才能增长到 7.5 微米。
需要宇宙的当前年龄才能增长到 7.5 微米。















![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)


![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)






