量子世界/影响与应用/量子弹跳球

量子弹跳球

作为一个具体的例子，考虑以下势能

$V(z)=mgz\quad {\hbox{if}}\quad z>0\quad {\hbox{and}}\quad V(z)=\infty \quad {\hbox{if}}\quad z<0.$

$g$ 是地面处的重力加速度。对于 $z<0,$，如上一节中给出的薛定谔方程告诉我们，$d^{2}\psi (z)/dz^{2}=\infty$，除非 $\psi (z)=0.$ 因此，对于负 $z$ 的唯一合理的解是 $\psi (z)=0.$ 要求 $V(z)=\infty$ 对于 $z<0$ 确保了我们完美的弹性、无摩擦的量子弹跳器不会被发现在地板以下。

因为一图胜千言，我们不会针对这个特定的势能求解时间无关的薛定谔方程，而只是绘制其前八个解

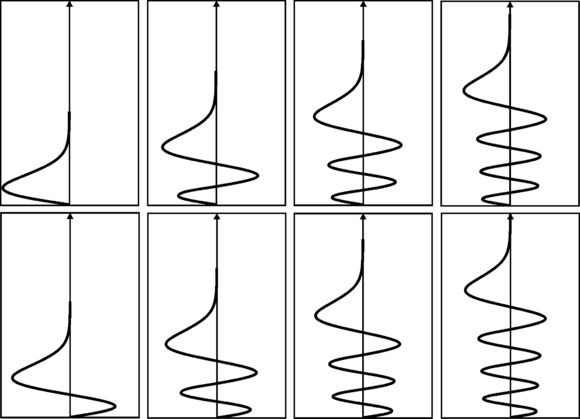
在相同的势能作用下，经典的弹跳球会在哪里反向运动？观察位置和动量（波数）之间的相关性。

所有这些状态都是稳态；在 $z$ 轴的任何特定区间内找到量子弹跳器的概率与时间无关。那么我们如何让它运动呢？

回想一下，薛定谔方程的任何线性组合都是另一个解。考虑这两个稳态的线性组合

$\psi (t,x)=A\,\psi _{1}(x)\,e^{-i\omega _{1}t}+B\,\psi _{2}(x)\,e^{-i\omega _{2}t}.$

假设系数 $A,B$ 和波函数 $\psi _{1}(x),\psi _{2}(x)$ 是实数，我们计算与 $\psi (t,x)$ 相关的粒子的平均位置

$\int \!dx\,\psi ^{*}x\psi =\int \!dx\,(A\psi _{1}e^{i\omega _{1}t}+B\psi _{2}e^{i\omega _{2}t})\,x\,(A\psi _{1}e^{-i\omega _{1}t}+B\psi _{2}e^{-i\omega _{2}t})$

$=A^{2}\int \!dx\,\psi _{1}^{2}\,x+B^{2}\int \!dx\,\psi _{2}^{2}\,x+AB(e^{i(\omega _{1}-\omega _{2})t}+e^{i(\omega _{2}-\omega _{1})t})\int \!dx\,\psi _{1}x\psi _{2}.$

前两个积分分别表示与$\psi _{1}(x)\,e^{i\omega _{1}t}$ 和 $\psi _{2}(x)\,e^{i\omega _{2}t},$ 相关的粒子的（与时间无关的）平均位置。最后一项等于

$2AB\cos(\Delta \omega \,t)\int \!dx\,\psi _{1}x\psi _{2},$

这告诉我们，粒子的平均位置以频率 $\Delta \omega =\omega _{2}-\omega _{1}$ 和振幅 $2AB\int \!dx\,\psi _{1}x\psi _{2}$ 在前两项之和附近振荡。

访问此网站以观察与最初与高斯分布相关的量子弹跳球相关的概率分布的时间依赖性。