量子世界/影响和应用/为什么能量是量子化的

为什么能量是量子化的

再次将自己限制在一个空间维度上，我们将时间无关薛定谔方程写成这种形式

${d^{2}\psi (x) \over dx^{2}}=A(x)\,\psi (x),\qquad A(x)={2m \over \hbar ^{2}}{\Big [}V(x)-E{\Big ]}.$

由于这个方程除了可能 $\psi$ 本身之外不包含复数，它有实数解，而这些解正是我们感兴趣的。你会注意到如果 $V>E,$ 那么 $A$ 为正，而 $\psi (x)$ 与它的二阶导数具有相同的符号。这意味着 $\psi (x)$ 图形在 $x$ 轴上方向上弯曲，在下方向下弯曲。因此它不能穿过轴。另一方面，如果 $V<E,$ 那么 $A$ 为负，而 $\psi (x)$ 与它的二阶导数具有相反的符号。在这种情况下，$\psi (x)$ 的图形在 $x$ 轴上方向下弯曲，在下方向上弯曲。结果，$\psi (x)$ 的图形不断穿过轴——它是一个波。此外，差值 $E-V,$ 越大，图形的曲率越大；曲率越大，波长越小。用粒子的术语来说，动能越高，动量越大。

现在让我们找到描述粒子“困”在势阱中的解——束缚态。考虑这种势

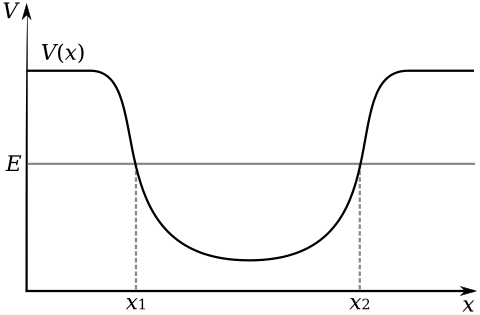
首先，观察在 $x_{1}$ 和 $x_{2},$ 处，其中 $E=V,$，$\psi (x)$ 的斜率没有变化，因为在这些点上， $d^{2}\psi (x)/dx^{2}=0$。这告诉我们，在这些点上，找到粒子的概率不会突然降至零。因此，可以在 $x_{1}$ 的左侧或 $x_{2},$ 的右侧找到粒子，而经典情况下是不可能发生的。（经典粒子会在这些点之间来回振荡。）

接下来，考虑由 $\psi (x)$ 定义的概率分布必须是可归一化的。对于 $\psi (x)$ 的图形，这意味着它必须随着 $x$ 渐近地逼近 $x$ 轴，即 $x\rightarrow \pm \infty .$

假设我们有一个特定值 $E.$ 的标准化解。如果我们增加或减少 $E,$ 的值，$\psi (x)$ 图像在 $x_{1}$ 和 $x_{2}$ 之间的曲率也会增加或减少。一个小的增加或减少不会给我们另一个解：$\psi (x)$ 不会在正负 $x.$ 处都渐近地消失。为了得到另一个解，我们必须增加 $E$ 恰好合适的量，以便在 "经典" 转折点 $x_{1}$ 和 $x_{2}$ 之间增加或减少一个波节，并使 $\psi (x)$ 在两个方向上再次渐近地消失。

底线是，束缚粒子的能量——被 "困" 在势阱中的粒子——是 *量子化* 的：只有某些值 $E_{k}$ 可以产生时间无关薛定谔方程的解 $\psi _{k}(x)$。