量子世界/影响与应用/氢原子

氢原子

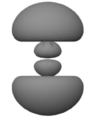
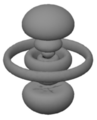
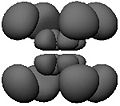
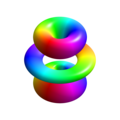虽然德布罗意在1923年的理论中提出了圆形电子波，但薛定谔在1926年的“波动力学”中提出了三维的驻波。找到它们意味着找到与时间无关的薛定谔方程的解

$E\psi (\mathbf {r} )=-{\hbar ^{2} \over 2m}\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)\psi (\mathbf {r} )+V(\mathbf {r} )\,\psi (\mathbf {r} ).$

其中 $V(\mathbf {r} )=-e^{2}/r,$ 是经典电子在距离质子 $r=|\mathbf {r} |$处的势能。（只有在我们进行相对论理论时，我们才能摆脱经典思维的最后残留。）

$E\psi (\mathbf {r} )=-{\hbar ^{2} \over 2m}\left({\frac {\partial ^{2}}{\partial x^{2}}}+{\frac {\partial ^{2}}{\partial y^{2}}}+{\frac {\partial ^{2}}{\partial z^{2}}}\right)\psi (\mathbf {r} )-{\frac {e^{2}}{r}}V(\mathbf {r} )\,\psi (\mathbf {r} ).$

在使用这个方程时，我们忽略了（i）电子对质子的影响，质子的质量是电子的1836倍，（ii）电子的自旋。由于相对论和自旋效应对氢原子的可测量性质的影响相当小，因此这种非相对论近似仍然能给出非常好的结果。

对于束缚态，总能量 $E$ 是负的，薛定谔方程有一组离散的解。事实证明，$E$ 的“允许”值正是玻尔在1913年获得的值

$E_{n}=-{1 \over n^{2}}\,{\mu e^{4} \over 2\hbar ^{2}},\qquad n=1,2,3,\dots$

然而，对于每个$n$，现在有$n^{2}$ 个线性无关的解。（如果$\psi _{1},\dots ,\psi _{k}$ 是无关的解，那么它们都不能写成其他解的线性组合$\sum a_{i}\psi _{i}$。）

具有不同$n$ 的解对应于不同的能量。什么物理差异对应于具有相同$n$ 的线性无关解？

使用极坐标，可以发现对于特定值$E_{n}$，所有解都是具有以下形式的解的线性组合

$\psi (r,\phi ,\theta )=e^{(i/\hbar )\,l_{z}\,\phi }\psi (r,\theta ).$

$l_{z}$ 被证明是另一个 *量子化* 变量，因为$e^{(i/\hbar )\,l_{z}\,\phi }=e^{(i/\hbar )\,l_{z}\,(\phi \pm 2\pi )}$ 意味着$l_{z}=m\hbar$ 其中$m=0,\pm 1,\pm 2,\dots$ 此外，$|m|$ 有一个上限，我们将在稍后看到。

正如将 $\psi (t,\mathbf {r} )$ 因式分解为 $e^{-(i/\hbar )\,E\,t}\,\psi (\mathbf {r} )$ 使得能够获得一个与 $t$ 无关的薛定谔方程，因此，将 $\psi (r,\phi ,\theta )$ 因式分解为 $e^{(i/\hbar )\,l_{z}\,\phi }\,\psi (r,\theta )$ 使得能够获得一个与 $\phi$ 无关的薛定谔方程。这包含另一个实参数 $\Lambda ,$ 除了 $m,$ 其“允许”的值由 $l(l+1)\hbar ^{2},$ 给出，其中 $l$ 是满足 $0\leq l\leq n-1.$ 的整数。 $m$ 的可能值的范围受不等式 $|m|\leq l.$ 限制。 因此，主量子数 $n,$，角动量量子数 $l,$ 以及所谓的磁量子数 $m$ 的可能值是

$n=1$	$l=0$	$m=0$
$n=2$	$l=0$	$m=0$
	$l=1$	$m=0,\pm 1$
$n=3$	$l=0$	$m=0$
	$l=1$	$m=0,\pm 1$
	$l=2$	$m=0,\pm 1,\pm 2$
$n=4$	$\dots$	$\dots$

每个可能的量子数集 $n,l,m$ 定义了一个唯一的波函数 $\psi _{nlm}(t,\mathbf {r} ),$ 并且它们一起构成薛定谔方程的一个完整的束缚态解集（$E<0$）具有 $V(\mathbf {r} )=-e^{2}/r.$ 以下图像展示了前三个 $l=0$ 状态的位置概率分布（未按比例绘制）。在它们下方是概率密度相对于 $r.$ 的图。观察到这些状态具有 $n-1$ 个节点，所有节点都是球形的，也就是说，它们是 $r.$ 常数的表面。（三维波的节点是二维表面。“概率波”的节点是 $\psi$ 符号改变的表面，因此概率密度 $|\psi |^{2}$ 变为零。）

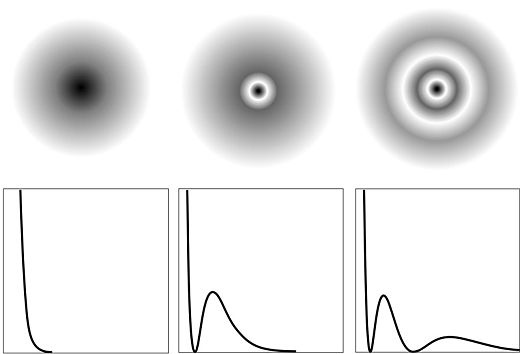
再仔细看看这些图像

• 
  $\rho _{2p0}$
• 
  $\rho _{3p0}$
• 
  $\rho _{3d0}$
• 
  $\rho _{4p0}$
• 
  $\rho _{2p0}$
• 
  $\rho _{3p0}$
• 
  $\rho _{3d0}$
• 
  $\rho _{4p0}$
• 
  $\rho _{4d0}$
• 
  $\rho _{4f0}$
• 
  $\rho _{5d0}$
• 
  $\rho _{5f0}$
• 
  $\rho _{4d0}$
• 
  $\rho _{4f0}$
• 
  $\rho _{5d0}$
• 
  $\rho _{5f0}$

字母 s、p、d、f 分别代表 l=0、1、2、3。（在理解原子光谱线的量子力学起源之前，人们区分了“锐线”、“主线”、“漫线”和“基线”。这些术语后来被发现对应于 $l$ 可以取的前四个值。从 $l=3$ 开始，标签按照字母表排列：f、g、h...) 可以看到，这些态同时具有球形节点和圆锥形节点，后者是 $\theta .$ 常数的曲面。（$\theta =0$ 的“圆锥形”节点是一个水平面。）这些态也总共有 $n-1$ 个节点，其中 $l$ 个是圆锥形的。

因为 $\phi$ 中的“波动性”包含在相位因子 $e^{im\phi },$ 中，因此它不会出现在 $|\psi |^{2}.$ 的表示中。为了使它可见，相位可以被编码为颜色

• 
  $\rho _{2p1}$
• 
  $\rho _{3p1}$
• 
  $\rho _{3d-1}$
• 
  $\rho _{4f-1}$
• 
  $\rho _{5f-2}$
• 
  $\rho _{6h-1}$
• 
  $\rho _{6h5}$

在化学中，通常考虑相反 $m$ 的真实叠加，例如 $\textstyle {\frac {1}{\sqrt {2}}}\left(e^{im\phi }+e^{i(-m)\phi }\right)={\sqrt {2}}\cos(m\phi )$，如以下图像所示，这些图像也是有效的解。

• 
  $\rho _{4f\pm 1}$ 或 $\rho _{4fxz^{2}}$
• 
  $\rho _{4f\pm 3}$ 或 $\rho _{4fx^{2}y}$
• 
  $\rho _{5f\pm 1}$ 或 $\rho _{5fxz^{2}}$
• 
  $\rho _{5f\pm 2}$
• 
  $\rho _{5f\pm 3}$ 或 $\rho _{5fx^{2}y}$
• 
  $\rho _{5g\pm 1}$
• 
  $\rho _{5g\pm 2}$
• 
  $\rho _{5g\pm 3}$

节点的总数再次为 $n-1,$，非球形节点的总数再次为 $l,$，但现在有 $m$ 个包含 $z$ 轴的平面节点和 $l-m$ 个锥形节点。

为什么 $z$ 轴如此特殊？实际上并没有，因为相对于不同轴定义的波函数 $\psi '_{nlm},$ 构成了另一个完整的束缚态解集。这意味着每个波函数 $\psi '_{nlm}$ 都可以写成函数 $\psi _{nlm},$ 的线性组合，反之亦然。