当没有抵消吸引力(如原子氢中原子核和电子之间的吸引力)时,我们将计算位置概率分布的模糊度随着相应动量模糊度的增加而增加的速率。
由于易于处理,我们选择一个高斯函数

它有一个钟形图。它定义了一个位置概率分布

如果我们对这个分布进行归一化,使  那么
那么  并且
并且

我们也有

 的傅里叶变换是
的傅里叶变换是 
- 它定义了动量概率分布

- 和

因此,与 相关的粒子的位置和动量的模糊度是"不确定性"关系所允许的最小值:
相关的粒子的位置和动量的模糊度是"不确定性"关系所允许的最小值:
现在回想一下

其中 它的傅里叶变换是
它的傅里叶变换是
![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
这定义了位置概率分布
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)
与 比较表明
比较表明 因此,
因此,
![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)
以下图表说明了与 分子或花生质量的物体相比,电子质量的粒子模糊度增长得有多快。这里我们看到了一个原因,虽然绝不是唯一的,即为什么就所有意图和目的而言,“一旦清晰,就永远清晰”对宏观物体的定位是正确的。
分子或花生质量的物体相比,电子质量的粒子模糊度增长得有多快。这里我们看到了一个原因,虽然绝不是唯一的,即为什么就所有意图和目的而言,“一旦清晰,就永远清晰”对宏观物体的定位是正确的。
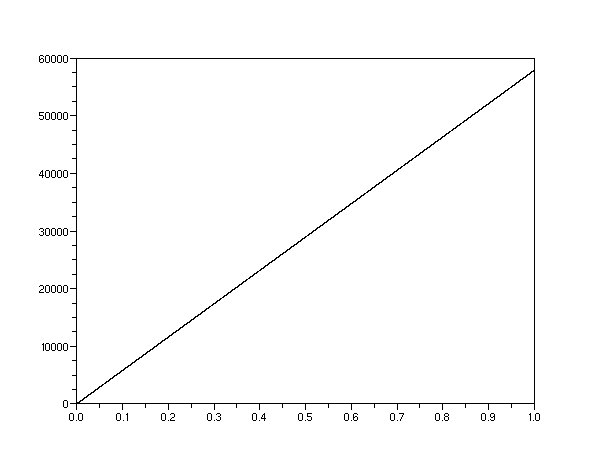
上图:一个电子,其  纳米。一秒钟后,
纳米。一秒钟后, 增长到近 60 公里。
增长到近 60 公里。
下图:一个电子,其  厘米。
厘米。  在一秒钟内仅增长了 16%。
在一秒钟内仅增长了 16%。

接下来,一个  分子,其
分子,其  纳米。一秒钟后,
纳米。一秒钟后, 增长到 4.4 厘米。
增长到 4.4 厘米。

最后,一个花生(2.8 克),其  纳米。
纳米。  需要宇宙目前的年龄才能增长到 7.5 微米。
需要宇宙目前的年龄才能增长到 7.5 微米。















![{\displaystyle \psi (t,x)={\sqrt {\sigma \over {\sqrt {\pi }}}}{1 \over {\sqrt {\sigma ^{2}+i\,(\hbar /m)\,t}}}\,e^{-x^{2}/2[\sigma ^{2}+i\,(\hbar /m)\,t]},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/110eec0173fbe62d9275715b0bcfc8cfcc7a8d57)
![{\displaystyle |\psi (t,x)|^{2}={1 \over {\sqrt {\pi }}{\sqrt {\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}}}}\,e^{-x^{2}/[\sigma ^{2}+(\hbar ^{2}/m^{2}\sigma ^{2})\,t^{2}]}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d10ad7738cf0a24ceb26ca00013f418a314f1f10)


![{\displaystyle \Delta x(t)={\sigma (t) \over {\sqrt {2}}}={\sqrt {{\sigma ^{2} \over 2}+{\hbar ^{2}t^{2} \over 2m^{2}\sigma ^{2}}}}={\sqrt {[\Delta x(0)]^{2}+{\hbar ^{2}t^{2} \over 4m^{2}[\Delta x(0)]^{2}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98b5229e5e6f530bf65df799679a76072ca2bd81)






