- 另见:效用应用于出行方式选择 (交通基础知识华夏公益教科书)
效用 是经济学家对消费者试图最大化的东西的表达。消费者可能想要更多的一种东西,而想要更少另一种东西。...
 无差异曲线
无差异曲线
需求取决于效用。效用函数表示一种将排名分配给不同组合的方法,使得更优选的组合排名高于不太优选的组合。效用函数可以用一般的方式表示为

其中  和
和  是商品(例如,旅行产生的净收益)
是商品(例如,旅行产生的净收益)
无差异曲线是消费者对之无差异的商品组合的轨迹。如果偏好满足通常的规律性条件(下面讨论),则存在一个效用函数  来表示这些偏好。无差异曲线上的点表示等效用。负斜率表示边际替代率 (MRS)
来表示这些偏好。无差异曲线上的点表示等效用。负斜率表示边际替代率 (MRS)

 替代品
替代品
 互补曲线
互补曲线
替代品将由

表示,其中无差异曲线的斜率 = -a/b。
从图形上来说,替代性越大,无差异曲线越接近直线。完全替代性是直线无差异曲线(例如,通过模式 A 或模式 B 出行上班)。
互补品由以下表示

互补性越高,无差异曲线越接近直角曲线;完全互补性将具有直角无差异曲线(例如,左右鞋,从家到工作和从工作到家的旅行)
贸易游戏是一种检查资源的经济交易如何影响个人效用的方法。假设经济包含以下资源(用彩色纸片表示)
- 白色
- 紫色
- 棕色
- 橙色
- 蓝色
- 灰色
- 绿色
- 黄色
- 金色
游戏的目标是最大化你的效用收益。
为自己定义一个效用函数

你会得到各种各样的资源
衡量你的效用
与班上的其他人进行交易(15分钟) 记录你的交易。
在交易期结束时再次衡量你的效用。计算你的绝对和百分比增长。
在黑板上记录分数
讨论
有没有更好的资源分配方式?
 预算约束
预算约束
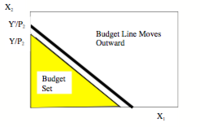 预算曲线向外移动
预算曲线向外移动
 预算曲线的斜率变化
预算曲线的斜率变化
 效用优化
效用优化
效用最大化涉及在资源约束下选择商品组合。例如,个人通过比较消费增加带来的效用增加与放弃资源(或等效地放弃这些资源可以购买的消费)带来的效用损失,来选择商品、服务和交通工具的数量。
通常将一个价格视为1,将一种商品视为货币。收入增加可以用预算线向外移动来表示。
商品 的价格上涨可以用预算线的斜率变化来表示(仍然固定在一个端点)。
的价格上涨可以用预算线的斜率变化来表示(仍然固定在一个端点)。
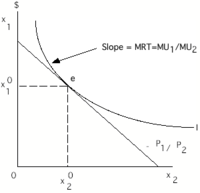
从图形上来说,优化过程是通过将个人愿意用一种商品交换另一种商品的比率与市场允许他/她进行交换的比率相等来实现的。这可以用下图来表示
个人通过沿着预算约束线向下移动到预算线的斜率( )——这是市场规定的交换比率——正好等于个人愿意用这两种商品进行交换的比率来最大化效用。这就是无差异曲线的斜率或边际转换率(MRT)。像 'e' 这样的点是一个效用最大化的均衡点。
)——这是市场规定的交换比率——正好等于个人愿意用这两种商品进行交换的比率来最大化效用。这就是无差异曲线的斜率或边际转换率(MRT)。像 'e' 这样的点是一个效用最大化的均衡点。
均衡点是无差异曲线/效用曲线与预算约束线的切点。
作为一个优化问题,可以写成

受以下条件约束

 在
在  中
中
其中
 = 价格向量,
= 价格向量, = 商品向量,
= 商品向量, = 收入
= 收入
(由于非饱和性,约束条件可以写成 px=m。)这种问题可以用拉格朗日乘子来解决
 其中
其中
 是拉格朗日乘子
是拉格朗日乘子
对  求导,并将一阶条件设为 0
求导,并将一阶条件设为 0

除以获得边际替代率和经济替代率






求解

或者

代入预算约束



马歇尔需求将价格和收入与需求束联系起来。这表示为  。此函数是 0 次齐次函数,因此如果我们将
。此函数是 0 次齐次函数,因此如果我们将  和
和  都加倍,
都加倍, 保持不变。我们可以开发一个间接效用函数
保持不变。我们可以开发一个间接效用函数

受以下约束:
其中求解此方程的 X 是需求束

进行单调变换

随收入增加而增加,随价格下降而下降
其中求解此方程的  是需求束
是需求束
间接效用函数  的属性
的属性
- 在
 中非递增,在
中非递增,在  中非递减
中非递减
- 0 次齐次函数
- 在
 中拟凸
中拟凸
- 在所有

间接效用函数的逆函数是支出函数 
约束条件:
支出函数  的性质
的性质
- 在
 中非递减
中非递减
- 在
 中具有 1 次齐次性
中具有 1 次齐次性
- 在
 中是凹的
中是凹的
- 在
 中是连续的,对于
中是连续的,对于 
希克斯需求或补偿需求用 h(p,u) 表示。

改变价格和收入以保持消费者在固定的效用水平,与马歇尔需求相比。罗伊恒等式允许在观察到的需求和效用之间来回转换



 达到
达到  的最小支出为
的最小支出为 
 从收入
从收入  获得的最大效用为
获得的最大效用为 
 在收入为
在收入为  时期的马歇尔需求与在效用为
时期的马歇尔需求与在效用为  时期的希克斯需求相同。
时期的希克斯需求相同。
 在效用为
在效用为  时期的希克斯需求与在收入为
时期的希克斯需求与在收入为  时期的马歇尔需求相同。
时期的马歇尔需求相同。
货币度量间接效用函数表明在价格水平为 p 时需要多少资金才能与在价格水平为 q 且收入为 m 时拥有相同的效用。将其定义为


注意 1 表示变化后,0 表示变化前
以当前价格为基准,需要多少收入变化才能获得相同的效用
 新的价格为基准,什么收入变化可以补偿价格变化
新的价格为基准,什么收入变化可以补偿价格变化
 效用和消费者剩余
效用和消费者剩余

通常

当效用是拟线性的 ( , 那么
, 那么

阿罗不可能定理 社会福利函数聚合问题的说明
三个个人都有良好的行为偏好。但是,将这三个聚合在一起并不会产生一个良好的行为偏好函数
- 甲喜欢红色胜过蓝色,蓝色胜过绿色
- 乙喜欢绿色胜过红色,红色胜过蓝色
- 丙喜欢蓝色胜过绿色,绿色胜过红色
聚合后,传递性被违反
- 两个人喜欢红色胜过蓝色
- 两个人喜欢蓝色胜过绿色,
- 两个人喜欢绿色胜过红色
社会想要什么?
定义一个消费集X,例如{房屋,汽车,电脑},
'x', 'y', 'z', 是商品组合,例如 x{房屋,汽车}, y{汽车,电脑}, z{房屋,电脑}。
商品本身并不被消费,而是为了相对于其他商品的属性而被消费
我们想要找到对组合进行排序的偏好。效用是序数,所以我们只关心哪个更大,而不是大多少。
对偏好有一些条件,以产生一个连续(良好行为)的效用函数。
- 完备性:或者
 (读作 x 比 y 更好)或者
(读作 x 比 y 更好)或者  或者两者都满足
或者两者都满足
- 自反性:

- 传递性:如果
 并且
并且  ,那么
,那么  (这对社会福利函数构成了一个问题)
(这对社会福利函数构成了一个问题)
- 单调性:如果
 ,那么
,那么 
- 局部非饱和:多总比少好
- 凸性:如果
 并且
并且  ,那么
,那么 
- 连续性:输入的微小变化会导致输出的微小变化。偏好关系
 在 X 中是连续的,如果它在极限运算下保持不变
在 X 中是连续的,如果它在极限运算下保持不变
如果函数 f 在其域中的点 a 处连续,则
 存在
存在

如果 'f' 在 'a' 处不连续,我们说 'f' 在 'a' 处不连续。













































































