三角学/将一个三角形转换为另一个

问题

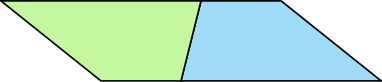
• 给定两个面积相同的三角形，我们可以将其中一个切成有限块，然后重新排列成另一个吗？

思考过程

如果我们可以将一个三角形切开并重新排列这些部分以形成一个矩形，那么我们做得很好。矩形很容易处理。如果我们可以得到一些小矩形，以某种方式将它们变成一边长度为 1 的矩形，然后将它们全部堆叠在这边上形成一个一边长度为 1 的矩形条，那么我们就赢了。为什么？因为切割和重新排列的过程是可逆的。具体来说

我们可以切割和重新排列第一个三角形，以形成一个面积相同且一边长度为 1 的矩形。我们可以对另一个做同样的事情。如果我们将此单位矩形的两种分割方式的切割线叠加起来，我们将得到可以重新排列成第一个三角形或第二个三角形的碎片。

好吧，我们可以将任何三角形切割成两个直角三角形，并且每个直角三角形都可以切割并重新组装以形成一个矩形。所以我们肯定可以从每个三角形中得到两个矩形。我们可以将这些切割成许多小矩形。

现在，我们如何将这些矩形转换为一边为一个单位的矩形？

一些实验表明，使用平行四边形是最佳方法。我们可以以一定角度切割，以获得我们想要的边长。而且我们可以切割平行四边形并重新组装成矩形，同时保持一边的长度。一旦我们想到使用平行四边形，并研究了切片和重新组装它们的方法，我们发现我们实际上不需要对矩形做任何特殊操作。以下是我们的做法。

备注

我们不必一开始就把我们的解剖分成小块。我们可以在进行时进行。然后，无论我们最终得到什么解决方案，我们都可以将其转换为我们一开始就解剖三角形的解决方案。

解决方案

将一个三角形转换为另一个的解决方案 移动 I 首先取一个面积为 A 的三角形，将其切成两块，然后使用移动 I重新组装成具有相同底边的平行四边形，如下所示 我们取了尺寸为一半的顶部三角形，并将其旋转了 180 度。 移动 II 现在，给定任何平行四边形，我们可以使用移动 II，切割和交换两个部分的顺序，该顺序保留底边并将顶边向左或向右移动至多底边的长度 更改一边的长度 通过重复移动 II足够多次，我们可以使不作为底边的边长变为任何我们想要的长度，只要它至少为$\displaystyle A/({\text{底边长度}})$。这不是一个非常严格的限制。我们的目标是得到一个平行四边形，它的一对边长为一个三角形的底边，而另一对边长为另一个三角形的底边。 为什么我们要这样做？因为然后我们得到一个平行四边形，它可以是第一个三角形或第二个三角形形成的。 可能会出现什么问题？唯一可能出现的问题是如果我们要得到的边长$\displaystyle <A/({\text{底边长度}})$。为了避免这种情况，我们将原始三角形定位，使每个三角形的最长边作为底边。然后通过使用移动 II一次或多次 (a) 我们不会更改底边长度，该长度与原始三角形的底边长度相同。 (b) 我们使另一对边长为第二个三角形的底边长度。 为了确认我们没有尝试将边长设置得过短，我们注意到，在每个三角形中，最长边必须至少与面积为 A 的等边三角形的边长相等。这是因为对于给定的面积，等边三角形在保持最长边最短方面做得最好。在等边三角形中，每条边都等于$\displaystyle {\sqrt {\frac {4A}{3}}}$。这两个三角形的最长边都必须至少等于$\displaystyle {\sqrt {\frac {4A}{3}}}$。最长边长度的乘积为$\displaystyle \geq {\frac {4A}{3}}>A$，因此我们没有尝试将边长设置得过短。 过渡 现在我们有一个平行四边形，它的底边等于其中一个三角形的底边，另一条边等于另一个三角形的底边。 我们已经完成了一半，将一个三角形转换为另一个三角形。我们可以翻转平行四边形，使另一条边作为底边。现在按照相反的步骤，以反向的 **移动 I** 结束，我们就将这些碎片重新组合成第二个三角形。

• 回到 希尔伯特的第三问题