三角学/爱好者/希尔伯特第三问题

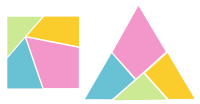
帽子商问题（右图）由谜题创作者亨利·杜德尼于 1907 年提出，它将三角形切割成正方形，只需三刀。

任何两个面积相同的二维多边形都可以被切割成不同的碎片，使得其中一个可以被重新组合成另一个。罕见的是，这种切割方式如此优雅。当你不在乎碎片数量时，找到切割方案并不难。

证明我们可以将任何两个面积相同的多边形切割成相同的碎片。

注意，我们总是可以将多边形切割成三角形。我们可以利用这个事实，只关注我们是否可以通过切割将一个三角形转换成另一个面积相同的三角形。
如果你在尝试将一个三角形转换成另一个三角形时卡住了，这里有一个可能的解决方案。在你尝试过这个问题之后再看它。

希尔伯特第三问题是，两个底面积和高都相同，因此体积也相同的四面体，是否可以被切割成四面体并重新组合成彼此。对于某些四面体对来说是可能的，但并非所有都如此。一个非常密切相关的問題是，一个立方体是否可以被切割成有限数量的碎片并重新组合成一个正四面体。事实证明，这是不可能的。

为了证明这一点，我们需要一些数学工具。

向量空间

在本页中，我们将使用有关向量空间的概念。

实数上的向量空间

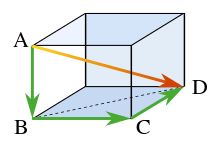
处理三维空间的一种数学方法是将其作为三维欧几里得空间 $\mathbb {R} \times \mathbb {R} \times \mathbb {R}$ ，也可以写成 $\mathbb {R} ^{3}$ 。空间中的一个点由三个数字表示，每个数字都是一个实数，比如 $\displaystyle 3$ 或者 $\displaystyle 6.18239013...$ 或者 $\displaystyle 1.414...$

对于 $\mathbb {R} ^{3}$ ，我们可以使用勾股定理计算距离 - 将每个坐标的平方加起来，然后取平方根。

也有一些公式可以计算不同方向之间的角度，以及各种类型的三维空间位置变换，例如绕原点旋转。 $\mathbb {R} ^{3}$ 是一个我们对事物如何运作有很大直觉的空间。

我们不必将自己局限于三维空间。我们可以拥有 $\mathbb {R} ^{109}$ 上的向量空间。许多关于 $\mathbb {R}$ 上向量空间的公式，无论是在 1、2、3 维还是更高维中，都适用。在这些情况下，用 $\mathbb {R} ^{n}$ 表述结果更经济，其中我们理解可以自由选择 n 的值。即使如此，我们通常使用 $\mathbb {R} ^{3}$ 而不是 $\mathbb {R} ^{109}$ 来帮助我们理解正在发生的事情。

关于向量空间的更多信息可以在《线性代数》一书中找到。
维基百科也提供了关于欧几里得空间的信息。

有理数上的向量空间

我们也可以在有理数上形成一个向量空间， $\mathbb {Q}$ 。

$\mathbb {Q}$ 包括像 $\displaystyle 1.3$ 这样的数字（它可以表示为有理数分数 $\displaystyle 13/10$ ），但不包括像 ${\sqrt {2}}=1.4142...$ 或 $\displaystyle 6.18239013...$ 这样的数字，我们假设 '...' 表示它以任意数字继续下去， $6.18239013...\notin \mathbb {Q}$ 。

在 $\mathbb {Q} ^{3}$ 中，坐标为 $\displaystyle (4.5,-7.1,9/7)$ 的点是允许的。坐标为 $\displaystyle (9.2,6.18239013...,8.1)$ 的点是不允许的，因为所有三个坐标都必须在 $\mathbb {Q}$ 中。

$\mathbb {Q}$ '遗漏了一些值' 这一事实对我们来说将非常重要，因为它将证明我们无法解剖任意四面体并重新组装成一个立方体。

无论我们使用 $\mathbb {R} ^{3}$ 还是 $\mathbb {Q} ^{3}$ ，我们使用“点”来表示相对于原点的位姿，并使用向量来表示两点之间的相对位移。我们可以对向量进行加法运算。我们可以对向量进行减法运算。我们可以用一个数字乘以一个向量，前提是该数字是正确的类型（在 $\mathbb {R}$ 或 $\mathbb {Q}$ 中分别为实数或有理数）。

为了研究希尔伯特的第三问题，我们需要一个关于 $\mathbb {Q}$ （有理数）的向量空间。像 $\displaystyle 3/4$ 和 $\displaystyle -1.125$ 这样的数字是允许的。像 $\displaystyle 6.18239013...$ 这样的数字是不允许的。

商空间

解释什么是商空间

不变量

多米诺骨牌

一个非常有用的工具，用于证明一个图形不能以特定方式细分，就是不变量的概念。它们可以用于例如多米诺骨牌问题中证明不可行性。

这里有一个简单的分割或细分谜题，其中一个不变量表明为什么解是不可行的。

在这个谜题中，目标是用 23 个多米诺骨牌（只有两个方格的多米诺骨牌）平铺选定的区域。

这是不可能的。

为什么平铺不能起作用（剧透）

剧透警告：我们即将给出简单而优雅的证明。如果您想先自己尝试一下，请停止阅读。如果不是，请继续阅读。如果我们将棋盘像棋盘一样着色，例如左上角为黑色，那么黑色方格比白色方格多两个。然而，每个多米诺骨牌覆盖一个白色方格和一个黑色方格。

黑色方格覆盖数与白色方格覆盖数之差是一个不变量。它在空棋盘上的初始值为零。当我们放置更多多米诺骨牌时，不变量保持不变。它确实是常数。它从零开始，并保持为零。然而，为了覆盖所有方格，它需要达到 2 - 这产生了矛盾。

其他不变量

在多米诺骨牌问题中，不变量只是一个数字。为了解决希尔伯特的第三问题，我们需要一个更复杂的不变量。我们需要一些能够同时捕捉角度和长度信息的东西。你可能认为复数可以满足要求，但实际上我们需要更多，因为涉及的长度不止一个。我们以一种专门针对我们正在解决的问题的方式构建了不变量的定义域。该定义域不是 R，也不是 C，而是一个我们构建的相当奇怪的数学对象，它正好具有我们需要的性质。

张量积

解释什么是张量积

德恩不变量

\operatorname {D} (P)=\sum _{e}\ell (e)\otimes (\theta (e)+\mathbb {Q} \pi )

它是常数

证明，由于我们以这种方式构建了它，因此当我们将多面体切成碎片时，它不会改变。