使用算盘/现代除法

引言和最初的方法

欧几里得除法

如果我们考虑两个自然数 $a$ 和 $b$ ， $a$ 除以 $b$ （表示为 $a/b$ 或 $a\div b$ ）回答了数字 $b$ 在数字 $a$ 中包含了多少次的问题。在 $a/b$ 中的数字 $a$ 称为被除数， $b$ 称为除数。答案称为商。

让我们以 $a=1225$ 和 $b=35$ 为例。除了重复减法并计算我们从被除数中减去除数的次数之外，没有更简单的方法来回答这个问题。我们可以使用算盘上的一个列作为计数器来直接进行操作。

1225÷35 = 35，原始方法
算盘	注释
ABCDEFGHIJKL
35 1225
+1 -35	从KL减去35，在计数器F中加1
35 1 1190
+1 -35	从KL减去35，在计数器F中加1
35 2 1155
+1 -35	从KL减去35，在计数器F中加1
35 3 1120
...	继续再进行33次...
35 33 70
+1 -35	从KL减去35，在计数器F中加1
35 34 35
+1 -35	从KL减去35，在计数器F中加1
35 35 00	完成，商数在EF中为35！

因此，我们发现数字 $35$ 在 $1225$ 中正好包含了 $35$ 次，因为我们不能继续减去 $35$ 而不会开始处理负数。因此，在这个例子中，商是： $q=35$ 。

正如我们所看到的，在这种情况下，我们可以写成 $1225=35\times 35$ 或者

$a=q\times b$

我们不能期望在一般情况下都能如此。如果我们用 $a=1240$ 重复这个过程，我们会看到，在减去 $35$ 乘以 $35$ 次后，算盘上会剩下 $15$ ，我们不能继续减去 $35$ 而不会进入负数。因此，我们有 $1240=35\times 35+15$ ；也就是说，将 $1240$ 除以 $35$ 的结果是商为 $35$ ，余数为余数 $15$ 。一般情况下，我们将有

$a=q\times b+r$

其中

$a$ ：被除数
$b$ ：除数
$q$ ：商
$r$ ：余数

如果余数为零，则被除数是除数的倍数。

这就是欧几里得除法在自然数上的概念，小数除法可以简化为自然数除法。

一些改进：分块方法

上一节中采用的方法在概念上是最简单的，但它极其冗长且效率低下。与其直接从被除数中减去除数 $b$ ( $35$ ) 开始，我们先考虑从被除数中减去除数的多少倍的10次幂；在我们的例子中：我们可以减去3500、350，还是只能减去35？显然我们可以减去350，我们将开始减去350个“块”，当我们无法继续时，我们将开始减去35个“块”，如下所示

1225÷35 = 35，这是一个很大的改进
算盘	注释
ABCDEFGHI
35 1225	开始，计数器在D处，
35 1 875	从GH中减去35，将计数器D加1，
35 2 525	从GH中减去35，将计数器D加1，
35 3 175	从GH中减去35，将计数器D加1，
35 31140	从HI中减去35，将计数器E加1，
35 32105	从HI中减去35，将计数器E加1，
35 33 70	从HI中减去35，将计数器E加1，
35 34 35	从HI中减去35，将计数器E加1，
35 35 00	从HI中减去35，将计数器E加1。
35 35	没有余数。完成，商为35！

这快多了（我们有意尽可能缩短计数器和被除数之间的距离。这在某种程度上模糊了过程，但使我们更接近于我们将在现代除法方法中常规执行的操作。请仔细研究以上计算，并使用你自己的算盘）。让我们从这里继续，寻找更高的效率。

如果我们能够轻松地将除数加倍并在记忆中保留它，那么我们可以通过减去一到两个除数“块”来缩短运算。

倍	块
1	35
2	70

1225÷35 = 35，更复杂的方法
算盘	注释
ABCDEFGHI
35 1225	开始，计数器在D处，
35 2 525	从GH中减去70，将计数器D加2，
35 3 175	从GH中减去35，将计数器D加1，
35 32105	从HI中减去70，将计数器E加2，
35 34 35	从HI中减去70，将计数器E加2，
35 35 00	从HI中减去35，将计数器E加1。
35 35	没有余数。完成，商为35！

或者，如果我们可以像下面这样通过将除数加倍三次来构建一个表格，则会更好^[1]

倍	块
1	35
2	70
4	140
8	280

1225÷35 = 35，一种非常有效的方法
算盘	注释
ABCDEFGHI
35 1225	开始，计数器在D处，
35 2 525	从GH中减去70，将计数器D加2，
35 3 175	从GH中减去35，将计数器D加1，
35 34 35	从HI中减去140，将计数器E加4，
35 35 00	从HI中减去35，将计数器E加1。
35 35	没有余数。完成，商为35！

这稍微简短一些，而且显然，没有什么比拥有除数的完整乘法表更快了

乘法表

35的乘法表
倍	块
1	35
2	70
3	105
4	140
5	175
6	210
7	245
8	280
9	315

然后

1225÷35 = 35，最短的方法！
算盘	注释
ABCDEFGHI
35 1225	开始，计数器在D处，
35 3 175	从GH中减去105，将计数器D加3，
35 35 00	从HI中减去175，将计数器E加5。
35 35	没有余数。完成，商为35！

毫无疑问，这是一种最佳的除法方法，一旦我们有了像上面那样的“块”表，就没有什么比它更快更方便的了。但是计算“块”表很费时间，需要纸和笔来书写，只有当我们需要对同一个除数进行大量的除法运算时，这项额外的工作才值得。

1617年，对数之父约翰·纳皮尔提出了他的发明来解决这个问题，该发明由一系列被称为纳皮尔算筹的算筹组成，上面写着一位数的乘法表，这些算筹可以组合起来得到任何数的乘法表。例如，在我们的例子中

使用纳皮尔算筹计算35的乘法表
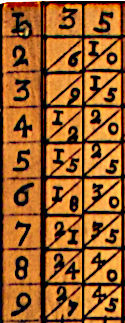
	1	35
	2	70
	3	105
	4	140
	5	175
	6	210
	7	245
	8	280
	9	315

毫无疑问，这样的发明传播到了东方，并与算盘一起使用，但这种用法必须被认为是例外的；并非每个人都能随时随地使用纳皮尔算筹。需要另一种工具，那就是传统的一位数乘法表，它是死记硬背下来的，我们将用它来近似表示除数的特定乘法表（上面使用的那个），这个表将指导我们选择必须尝试的商的数字。

需要注意的是，以上过程并没有穷尽分块方法的所有可能性。如果你阅读了《整数长除法的权威高等数学指南》^[2]文章，你将会对可以执行的各种除法方法感到惊讶。

现代除法

现代除法与传统除法

现代除法方法之所以被称为现代，是因为在整个20世纪上半叶，它的使用取代了传统方法，但实际上它比这古老得多，在13世纪被传统方法取代。现代方法的一个特点是使用一位数乘法表作为我们必须尝试的中间商数的选择指南，以及计算我们必须从被除数中减去的“块”。

十进制乘法表
×	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9
2	2	4	6	8	10	12	14	16	18
3	3	6	9	12	15	18	21	24	27
4	4	8	12	16	20	24	28	32	36
5	5	10	15	20	25	30	35	40	45
6	6	12	18	24	30	36	42	48	54
7	7	14	21	28	35	42	49	56	63
8	8	16	24	32	40	48	56	64	72
9	9	18	27	36	45	54	63	72	81

相比之下，传统方法既使用特殊的除法表作为中间商数的指南，也使用乘法表来计算要减去的“块”。

明治维新后，现代方法在日本开始取代传统方法的主要原因是，对于那些已经掌握了纸笔除法的人来说，它更容易更快地学习，因为它不需要记忆复杂的除法表。另一方面，传统方法使除法成为一个完全自动化的过程，无需思考，只需要遵循规则即可得到结果，从而使操作无需任何脑力疲劳。如果你对这个话题感兴趣，可以参考维基教科书：传统算盘和珠算。

算盘除法的关键点

学习算盘的关键点之一是要意识到，这种工具使我们能够非常快速地纠正一些错误，并且不留下痕迹，这使得算盘成为一种特别适合试错过程的工具。这在除法的情况下尤其有用。因此，如果我们必须计算634263÷79283，我们不必绞尽脑汁去寻找正确的商数，只需通过将原始问题简化为63÷7来选择一个近似的临时或中间数字，然后通过尝试从被除数中减去“块”（中间商数）✕79283来测试它；以下情况之一将会发生

中间商数是正确的: 也就是说，我们可以减去“块”（中间商数）✕（除数）而不会出现负数，但我们不能再减去一次商数，因为余数小于除数。
它是不够的，我们需要向上修正: 我们可以减去“块”（中间商数）✕（除数）而不会出现负数，但我们仍然可以再减去一次商数，因为余数大于/等于除数。我们将中间商数加1，然后再次从余数中减去除数。
它是过大的，我们需要向下修正: 这是最复杂和最容易出错的情况。我们通常在（减去“块”的过程中）发现得太晚，中间数字过大，我们需要回退，将商数减1，并通过加上多减的部分来恢复被除数/余数，然后才能继续。

因此，获得商数的一个数字的过程有两个阶段

选择一个中间商数。
测试它是否正确，如果不正确则修改它。

一旦我们找到了正确的数字，我们通常会得到一个非零的余数，如果我们想将除法扩展到商数的下一位，这个余数将充当被除数。

我们将在接下来的示例中看到所有这些，但首先，我们需要简单介绍一下如何在算盘上组织除法。

现代除法排列

被除数是我们在算盘上要操作的活动项，除数是不活动的，在操作过程中保持不变，事实上，它不需要输入到算盘中，但建议这样做，尤其对于初学者来说。与乘法一样，在算盘上放置被除数和除数有两种方式，每种方式都有其优点和缺点。

传统中式排列

除数放在算盘的最右边，而被除数放在左边，在其左边至少留出两列空位。

**1225÷35 中式排列**
A	B	C	D	E	F	G	H	I	K	J	L	M

		1	2	2	5						3	5

传统日式排列

除数位于算盘的最左边，被除数在其右边，两项之间至少留出四列空位。

**1225÷35 日式排列**
A	B	C	D	E	F	G	H	I	K	J	L	M

3	5					1	2	2	5

本书中，示例将使用日式风格，但您可以随意尝试两种方法。

放置商数

中间商数放置在被除数左侧的两列之一。为了确定哪一列，我们需要将除数与被除数前几位数相同的数字进行比较，如果需要，在其右侧添加零；称之为**工作被除数**。

工作被除数大于或等于除数: 这意味着除数可以整除工作被除数，商数（即除数可以整除工作被除数的次数）排列在被除数第一位数字左侧的第二列。; **示例**：827÷46，工作被除数82大于46，则中间商数位于被除数左侧的第二列。乘法表建议我们使用**2**作为中间商数（将827÷46简化为8÷4）

827÷46
算盘	注释
ABCDEFGHIJKLM
46 827
46 2 827	将中间商数2放在E列

工作被除数小于除数: 这意味着除数不能整除工作被除数。在这种情况下，我们需要将被除数的下一位数字（如果没有剩余数字，则为零）包含在我们的工作被除数中，商数（即除数可以整除此扩展工作被除数的次数）排列在被除数第一位数字左侧的列中。; **示例**：18÷467，180小于467，则工作被除数为1800，中间商数位于被除数左侧的第一列。乘法表建议我们使用**4**作为中间商数，在将1800÷467简化为18÷4之后。

标题文本
算盘	注释
ABCDEFGHIJKLM
467 18
467 418	将中间商数4放在G列

示例

您应该先进行一位数除数的练习，然后再尝试两位数、三位数等的除数。对于一位数除数，您永远不需要向上或向下修正。例如，您可以将123456789除以数字2、3、…、9。让我们在这里看看除以9的情况。

示例：123456789÷9 = 13717421

请将“->”符号理解为：“乘法表建议使用…”。
您会看到，在除最后一个之外的所有情况下，工作被除数都小于除数，我们需要将其扩展到两位数。

123456789÷9 = 13717421
算盘	注释
ABCDEFGHIJKLMNO
9 123456789	12/9 -> 1 作为中间商数
9 1123456789	将中间商数放在E列
-9	从FG列减去9✕1=9
9 1 33456789	33/9 -> 3 作为中间商数
9 1333456789	将中间商数放在F列
-27	从GH列减去9✕3=27
9 13 6456789	64/9 -> 7 作为中间商数
9 1376456789	将中间商数放在G列
-63	从HI列减去9✕7=63
9 137 156789	15/9 -> 1 作为中间商数
9 1371156789	将中间商数放在H列
-9	从IJ列减去9✕1=9
9 1371 66789	66/9 -> 7 作为中间商数
9 1371766789	将中间商数放在I列
-63	从JK列减去9✕7=63
9 13717 3789	37/9 -> 4 作为中间商数
9 1371743789	将中间商数放在J列
-36	从KL列减去9✕4=36
9 137174 189	18/9 -> 2 作为中间商数
9 1371742189	将中间商数放在K列
-18	从LM列减去9✕2=18
9 1371742 9	9/9 -> 1 作为中间商数
9 13717421 9	将中间商数放在L列
-9	从MN列减去9✕1=9
9 13717421	没有余数！完成 123456789÷9 = 13717421

123456789是一个有趣的数字，它恰好是9乘以13717421的积，后者是一个很大的质数！

示例：1225÷35 = 35 两位数除数。向下和向上修正

1225÷35 = 35
算盘	注释
ABCDEFGHIJ
35 1225	12÷3↦4 作为中间商数
+4	将中间商数输入F列
35 41225	现在尝试从GHI列减去4✕35的部分积，
-12	首先从GH列减去4✕3
35 40025	然后从HI列减去4✕5
-20	无法减去！
-1	向下修正中间商数的数字
35 30025
+3	将从GH列减去的多余部分返回^a
35 30325
-15	继续正常操作，从HI列减去3✕5
35 3 175	17÷3↦5 作为中间商数
+5	将中间商数输入G列
35 35175	尝试从HIJ列减去5✕35的部分积
-15	首先从HI列减去5✕3
35 35025
-25	然后从IJ列减去5✕5
35 35	没有余数，完成！1225÷35 = 35

注意：^a 我们已经从FGH列减去了4 × 3 = 12，但如果正确的商数数字是3，我们应该减去3 × 3 = 9，所以我们多减去了3（只是除数的第一位数字）。在继续之前，我们必须将这个多减的部分返回。

现在，假设在我们“糟糕的经历”之后，向下修正了商数的第一位数字，并且出于谨慎，我们选择4作为第二个中间商数，而不是乘法表建议的5。然后我们继续这样操作

1225÷35 = 35，第二个商数数字，向上修正的示例
算盘	注释
ABCDEFGHI
35 3 175	17÷3 -> 5，但我们使用4！
+4	将中间商数输入G列
35 34175	尝试从HIJ列减去4✕35的部分积
-12	首先从HI列减去4✕3 = 12
-20	然后从IJ列减去4✕5 = 20
35 34 35	余数大于或等于除数！
+1	向上修正G列
-35	从余数HI列减去除数
35 35	没有余数，完成！

示例 1÷327

到目前为止，我们已经考虑了自然数之间的除法，包括商数和余数以及自然数，但我们可以像在用长除法进行书面计算时那样，完全使用小数进行运算。例如，让我们在有13列的算盘上求327的倒数；即，1/327。

1÷327 = 0.00305810...
算盘	注释
ABCDEFGHIJKLM
327 1	10/3 -> 3 作为中间商数
327 31	将中间商数输入G列
-09	从HI列减去3✕3=9
327 3 1
-06	从IJ列减去3✕2=6
327 3 4
-21	从JK列减去3✕7=21
327 3 19	19/3 -> 6 作为中间商数
327 30619	将中间商数输入I列
-18	从JK列减去6✕3=18
327 306 1
-12	无法减去6✕2=12 从KL列！
-1	向下修正I列
+3	将从JK列减去的多余部分返回
327 305 4
-10	继续正常操作，从KL列减去5✕2=10
327 305 30
-35	从LM列减去5✕7=35
327 305 265	36/3 -> 8 作为中间商数
327 3058265	将中间商输入到J柱
-24	从KL柱减去8✕3=24
327 3058 25
-16	从LM柱减去8✕2=16
327 3058 9	无法继续！结果：3058

我们已经得到了 $3058$ 作为 $1/327$ 的前几位数字，但是 $1/327\approx 1/300=1/(3\cdot 100)=(1/3)\cdot 0.01\approx 0.33\cdot 0.01=0.0033$ ，所以我们的结果实际上是 $0.003058$ 。请参见下文关于如何找到除法中个位数所在位置的规则。

示例：634263÷79283 = 7,999987...，一个棘手的例子

最后，让我们求出这个特别恶意的除法商的第一位数字

634263÷79283 = 7,999987...
算盘	注释
ABCDEFGHIJKLM
79283 634263	63/7 -> 试9
79283 9634263
-63	从HI柱减去9*7=63
79283 9004263
-81	无法减去9*9=81从IJ柱！
-1	向下修正D柱
+7	恢复从余数中减去的过多部分
79283 8 74263
-72	继续从IJ柱减去8x9=72
79283 8 02263
-16	从JK柱减去8*2=16
79283 8 00663
-64	从KL柱减去8*8=64
79283 8 00023	无法减去8*3=24从LM柱！
-1	向下修正D柱
+7928	恢复从余数中减去的过多部分
79283 7 79303
-21	继续从LM柱减去7x3=21
79283 7 79282	商：7，余数：79282

毫无疑问，在这种情况下，将除数79283四舍五入到80000会给我们带来更好的结果，因为63÷/8建议使用7（正确数字）作为中间商数字。

634263÷79283 = 7,999987...，四舍五入除数
算盘	注释
ABCDEFGHIJKLM
79283 634263	63/8 -> 试7
7634263
-49	从HI柱减去7*7=49
79283 7144263
-63	从IJ柱减去7*9=63
79283 7 81263
-14	从JK柱减去7*2=14
79283 7 79863
-56	从KL柱减去7*8=56
79283 7 79303
-21	从LM柱减去7*3=21
79283 7 79282	商：7，余数：79282

个位数和十进制

寻找乘法中个位数所在位置的规则的对应规则是除法中的以下规则

商的个位数所在列位于被除数的个位数所在列的左侧

n+1

列；其中

n

是被除数小数点左侧的数字个数（可以为负数！）。

下表显示了一些除数的 $n$ 值


乘数	n
32.7	2
3.27	1
0.327	0
0.00327	-2

示例：1/327（我们在上面已经看到过）

1/327个位数
算盘	注释
ABCDEFGHIJKLM
327 1	除数有3位数。n=3
.	被除数个位数
...
327 3058 9	除法结束。结果：3058
.	被除数个位数
<---	将其向左移动n+1 = 4个位置
.	商的个位数
3058	以便这个...
.003058	...应该读作0.003058

乘法和除法作为互逆运算

在书面计算中，我们总是可以复查我们的计算，以确保我们没有犯错误，并且获得的结果是正确的。在使用算盘进行计算时，这是不可能的，因为算盘不会保留过去和中间结果的记忆。我们可以求助于一些健全性测试，例如九去法或十一去法，但使用算盘检查结果的传统方法一直是重复计算或撤消计算。

撤消加法和减法就像从结果开始，减去我们加过的数，加上我们减过的数一样简单；如果我们正确地进行计算和验证，我们应该最终得到一个重置的算盘。为了验证乘法，我们将使用除法，反之亦然，为了验证除法，我们将使用乘法，加上如果有的话的余数。完成此操作后，我们将算盘恢复到其初始状态，并将两个原始操作数恢复到其初始位置。让我们看一个例子

通过乘法测试2461÷64
算盘	注释
ABCDEFGHIJ
64 2461	24/6 -> 4作为中间商
42461	将中间商数输入F列
-24	从GH柱减去4✕6=24
64 4 61
-16	无法从HI柱减去4✕4=16
-1	向下修正中间商数字
64 3 61
+6	将从GH柱减去的过多部分返回
64 3 661
-12	继续正常操作，从HI柱减去3✕4=12
64 3 541	54/6 -> 9，但我们将使用8
64 38541
-48	从HI柱减去8✕6=48
64 38 61
-32	从IJ柱减去8✕4=32
64 38 29	商：38，余数29
	通过乘法进行复查从这里开始！
+48	将8✕6=48加到HI柱
64 38509
+32	将8✕4=32加到IJ柱
64 38541
64 3 541	清零G柱
+18	将3✕6=18加到GH柱
64 32341
+12	将3✕4=12加到HI柱
64 32461
64 2461	清零F柱。初始状态！

本书建议在使用一位数进行乘法和除法的第一次练习中使用数字123456789。尝试将其与反运算结合起来；例如：将123456789除以9得到13717421，并将此结果乘以9得到123456789，回到算盘上的相同起始位置。或者从将123456789乘以9开始得到1111111101，然后除以9回到起点。尝试从2到9的所有数字。

参考文献

↑ Wilson, Jeff. "长除法教学辅助，"双除法"". 双除法. 存档于原始文件，于 2021年3月2日。 {{cite web}}: 请检查日期值：|archivedate= (帮助); 忽略了“2005年”文本 (帮助); 忽略了未知参数|accesdate= (|access-date= 建议) (帮助)
↑ "关于整数长除法（及其变体）的权威高等数学指南". 数学保险库. 存档于原始文件，于 2021年5月14日。 {{cite web}}: 忽略了未知参数|accesdate= (|access-date= 建议) (帮助); 忽略了未知参数|name= (帮助)

外部链接

练习题

"生成器". 练习算盘. {{cite web}}: 忽略了未知参数|accesdate= (|access-date= 建议) (帮助)

进一步阅读

Kojima, Takashi (1954), "除法", 日本算盘：其使用和理论, 东京：查尔斯·E·塔特尔公司，ISBN 978-0-8048-0278-9
Heffelfinger, Totton (2004). "除法". 算盘：珠子的奥秘. 存档于原始文件，于 2021年6月29日。 {{cite web}}: 忽略了未知参数|accesdate= (|access-date= 建议) (帮助)
Siqueira, Edvaldo (2004). "小数和除法". 算盘：珠子的奥秘. 存档于原始文件，于 2021年5月6日。 {{cite web}}: 忽略了未知参数|accesdate= (|access-date= 建议) (帮助)

下一页：使用算盘 | 上一页：现代乘法
首页：使用算盘

[IDchunk-1] Wilson, Jeff. "长除法教学辅助，"双除法"". 双除法. 存档于原始文件，于 2021年3月2日。 {{cite web}}: 请检查日期值：|archivedate= (帮助); 忽略了“2005年”文本 (帮助); 忽略了未知参数|accesdate= (|access-date= 建议) (帮助)

[2] "关于整数长除法（及其变体）的权威高等数学指南". 数学保险库. 存档于原始文件，于 2021年5月14日。 {{cite web}}: 忽略了未知参数|accesdate= (|access-date= 建议) (帮助); 忽略了未知参数|name= (帮助)

[1]

[2]

a