 切线的斜率可以用逼近切线的割线来近似。
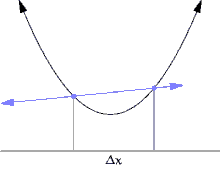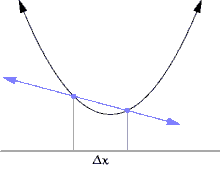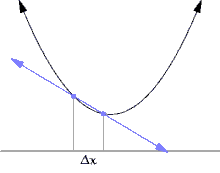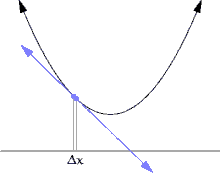
切线的斜率可以用逼近切线的割线来近似。
曲线上的一个点的斜率等于该点切线的斜率。由于直接测量切线的斜率很困难,我们使用割线来近似它。割线是在曲线上的两个点之间的一条线。
假设我们想要找到坐标为 的点的斜率。我们可以使用经过
的点的斜率。我们可以使用经过 和
和 的割线来近似它,其中
的割线来近似它,其中 是
是 的一个微小变化,而
的一个微小变化,而 是由此产生的
是由此产生的 的微小变化。
的微小变化。
割线的斜率为 。当
。当 越来越小时,
越来越小时, 接近点
接近点 的斜率。
的斜率。
当  趋近于零时,
趋近于零时, 的 极限 是我们所要找的值:点
的 极限 是我们所要找的值:点  的梯度。对于任意点
的梯度。对于任意点  ,梯度可以用导数表示。
,梯度可以用导数表示。
函数  的 导数
的 导数  是一个函数,它提供了
是一个函数,它提供了  所产生的曲线在点
所产生的曲线在点  的梯度。导数的正式定义为
的梯度。导数的正式定义为 
表示函数导数主要有两种方式: 和
和  。它们都表示相同的意思:
。它们都表示相同的意思: 关于
关于  的导数。
的导数。
以下是一些简单的规则,可以使复杂表达式的求导更容易。

例如,

例如,

例如,

例如,
切线是一条经过给定点的直线,它的斜率等于曲线在该点的斜率。法线是一条经过给定点的直线,它垂直于曲线在该点的切线。
要找到曲线在特定点处的切线或法线的方程,我们可以使用我们在坐标几何中使用的直线方程。
例如,求曲线 在点
在点 处的切线和法线的方程。
处的切线和法线的方程。

递增函数是指斜率始终大于或等于零的函数。
递减函数是指斜率始终小于或等于零的函数。
一个量的变化率是指该量关于时间的导数。例如,如果水以每秒 1 升的速度流入桶中,那么桶中水量的变化率就是每秒 1 升。
在某些情况下,两个量的变化率是相互关联的。例如,一个半径变化的圆将具有一个取决于半径的变化面积。圆的面积与半径的关系为  。如果半径以每秒 3 厘米的速度增长,它的变化率为
。如果半径以每秒 3 厘米的速度增长,它的变化率为  。可以使用链式法则求出面积的变化率
。可以使用链式法则求出面积的变化率

如果半径以每秒 3 厘米的速度增长,并且当前为 5 厘米,则面积的变化率为  平方厘米/秒。
平方厘米/秒。
 图上最大值和最小值的一个例子
图上最大值和最小值的一个例子
驻点是指曲线上的斜率为零的点。这意味着该点处的函数导数等于零。
驻点要么是最大值,要么是最小值。最大值是指函数达到最大值的地方。最小值是指函数达到最小值的地方。我们可以通过查看二阶导数来确定驻点是最大值还是最小值。
如果二阶导数为正,则斜率随着输入的增加而增加,因此驻点是极小值。
如果二阶导数为负,则斜率随着输入的增加而减小,因此驻点是极大值。
绘制曲线图时,驻点很有用。通过标记驻点,我们可以比其他方法更准确地绘制图形。
← 级数 · 积分 →































