结合代数/分裂二元数

平面代数

方程 jj=1 表达一个对合，一个在迭代时返回到原点的运算。当 1 被视为单位矩阵时，矩阵方程 mm = 单位矩阵有很多解（即使在 2x2 的情况下），这样的解就是一个对合矩阵。

分裂二元数利用了这种额外解的概念（超越 1 和负 1）来生成数字集 {x + jy: x,y 在 R 中}。根据

(u+jv)(x+jy) = ux + yv + j(uy + xv)

进行逐分量加法和乘法，这里称为分裂二元数的 2-代数，在百科全书中被称为分裂复数，那里还提供了一系列同义词。

为了描述分裂二元数平面的可逆元素，必须从平面中划去两条线 x=y 和 y=−x。在这样形成的四个象限中，包含 1+0j 的一个最为重要，因为任何单位的平方都位于该象限。在其中，集合

G = {exp(aj): a 在 R 中} 形成一个单参数群

exp(aj) exp(bj) = exp((a+b)j).

G ∪ −G 是单位双曲线 $x^{2}-y^{2}=1\ ,$，但用双曲函数参数化。

共轭双曲线是 jG ∪ −jG，也表示为 $\{x+jy:y^{2}-x^{2}=1\}.$

在除法二元数中，垂直和正交是同义词，但在分裂二元数中，正交在几何上有所不同，但在代数上是一致的：两个单位z 和w 是正交的，如果zw* 的实部为 0。双线性形式表示 <z,w> = 0。例如，对于任何g 在G 中，

g(jg)* = −j gg* = −j exp(aj) exp(−aj) = − j，其实部为零。

练习:

1. 证明单位群U = FxPxG，其中P 是正实数的乘法群，F = {j, −j, 1, −1}，是四元群。
2. 证明x + jy 位于单位所在的象限，当且仅当 y < |x|。
3. 证明乘以 j 的效果是在对角线 x=y 上翻转平面。
4. 对于g= cosh a + j sinh a，证明当a 增大时，正交点g 和 jg 收敛于渐近线。

同时性

当赫尔曼·闵可夫斯基使用世界线的概念来描述某个物体在时间中的轨迹来开发他的宇宙模型时，他认为运动物体的时间空间取决于其速度。因此，同时性相对于运动的观察者而言是相对的。分裂二元数中的正交性对应于速度向量与其独特的时间空间之间的关系。术语双曲正交性被用来区分它与垂直性。时间空间被称为时间超平面，因为它是在闵可夫斯基宇宙中的一个三维子空间。

G 的元素可用于在平面上形成群作用。这种作用有时被称为双曲旋转，因为对于任何常数k，双曲线 {u : u u* = k ≠ 0} 在u -> gu 下是不变集。但是，这种作用不会混合象限，因此术语旋转并不恰当。另一个效果是，垂直于y=x 的维度被压缩或挤压，正如收敛的正交向量g 和 jg 所证明的那样，其中g = exp(aj) 且a 正在增加。因此，当方向合适时，使用术语压缩映射。

面积

鉴于 j² = +1，因此当n 为偶数时，jⁿ 为 1，当n 为奇数时，jⁿ 等于 j。因此

$\exp(aj)\ =\ \cosh a+j\sinh a$ 因为 j 的幂将偶数项和奇数项分开。

变量a 是沿着单位双曲线 $x^{2}-y^{2}=1.$ 的双曲角。这种配置是自然双曲线的标准化形式，其中现在乘法单位距离原点一个单位距离，因此扇区面积是角度大小的一半，因为标准化。

在 D 中，乘法进行压缩，而不是压缩映射保留自然双曲线的扇区面积。狭义相对论中速度加法的重新线性化使用了 D 中单位双曲线的参数化。实际上，如果两个快度a 和b 相加，结果将根据$e^{aj}\ e^{bj}=e^{(a+b)j}$ 在 D 中相加。

D 中的正交性概念在算术上与 C 中的条件一致，但表示的是双曲正交性，即世界线与其时间超平面的关系。尽管只有二维，但分裂二元数有助于理解狭义相对论。

练习

单位双曲线 右支在 D 上的群作用对应于 R² 上的压缩映射 σ。

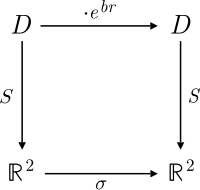
1. 矩阵 $S={\begin{pmatrix}1&1\\1&-1\end{pmatrix}}$ 且 σ 是 R² 上的压缩映射。证明矩阵S 提供了一个映射，使得 D 和 (R², xy) 作为环和二次空间同构，但S 不是欧几里得度量的实平面上的等距。

2. 对于K ⊂ D，area(K) 有限，以及 R 中的任何a 且u = exp(aj)，证明 {u k : k 在 K 中} 的面积等于K 的面积。

3. 双曲角与调和级数$\sum _{n=1}^{\infty }1/n\ ?$  有什么共同之处？答案：无界。比较它们的几何形状。

4. 绘制子群$\{pj^{n}e^{aj}:p>0,\ n=0,1,\ a\in R\}\subset U.$