核医学基础物理/核医学动力学研究

引言

这是维基教科书中名为 核医学基础物理 的一个正在开发的章节。

人体中物质的 代谢 是许多相互关联的动态过程的结果，包括物质的吸收、分布、利用、降解和排泄。仅测量其中一个参数可能会得到一个表明疾病的结果，但可能无法确定疾病的实际原因。当获得完整代谢系统的知识时，可能会确定有关原因的更详细信息。获得这种知识的一种方法是通过对生理系统的数学模拟。这种方法的结果包括生成整个系统的表示以及对系统组成部分之间相互作用的理解。这种方法通常涉及

1. 在通过添加合适的示踪剂刺激系统后获取实验数据；
2. 将实验数据与数学模拟预测的数据进行比较；以及
3. 使用诸如 最小二乘法、最大似然法 和 蒙特卡罗模拟 等方法，改变模拟参数，直到两组数据尽可能地一致。

这种方法的一般假设是

• 示踪剂的添加不会扰乱系统；
• 被追踪物（即正在研究的物质）在整个过程中是守恒的；
• 示踪剂在整个过程中是守恒的——允许放射性衰变；以及
• 系统处于稳态（即系统每个隔室中被追踪物的量保持恒定，每个隔室之间被追踪物的交换也保持恒定）。

目前使用两种主要类型的数学模型

• • 确定性：其中使用解析表达式来描述示踪剂在系统每个部分随时间的精确行为。使用的数学表达式通常是指数函数或幂函数；

• • 随机：其中系统的行为由随机过程决定，随机过程由概率函数描述。

下面将详细讨论确定性模型。

隔室分析

这种形式的确定性分析涉及将生理系统划分为多个相互连接的隔室——其中隔室定义为系统的任何解剖、生理、化学或物理细分。一个基本假设是示踪剂在整个隔室中均匀分布。最简单的系统是单隔室模型。我们将从这个简单的模型开始处理，然后扩展到更复杂的模型——最初的模型仅是为了开发框架，而后的模型则与核医学动力学研究直接相关；它们的获取和分析。

有一个名为 Compartments_TP 的 ImageJ 插件可用，它提供了对许多其他模型的模拟。

单隔室模型

示踪剂通过血管的流动，在理想的脉冲注射后，在下图中显示为单隔室模型的示例。图中所示的隔室是封闭的，除了被追踪物的流入和流出，示踪剂如箭头所示注入。在这些理论条件下，示踪剂将在注射后立即并在整个隔室中均匀混合。其数量将随着时间的推移而减少，这取决于流出的速率。图中使用的变量是

q：时间t时隔室中示踪剂的数量；以及
F：流出。

单隔室模型

我们可以将周转率k定义为这两个参数的比率，即

$k={\frac {-dq/dt}{q}}$

可以改写为

${\frac {dq}{dt}}=-kq$

无需详细介绍数学细节（与 放射性衰变定律 的推导类似！），该方程的解是

$q=q_{0}\ exp(-kt)\,\!$

其中q_o是时间t = 0时存在的示踪剂数量。

下图绘制了该方程，以说明周转率k的值的影响。

示踪剂数量 q 相对于时间的图形说明，对于周转率 k 的相对高低值。

<

该图表明，在注射后，隔室中的示踪剂数量将随时间呈指数下降，下降速率取决于流出，这可能符合直觉预期。

双隔室模型 - 闭合系统

一套更复杂，但仍然相对简单的模型是基于两个隔室的模型。在闭合系统中，示踪剂只是在两个隔室之间移动，而不会有任何整体损失或增益——见下图

闭合双隔室模型

因此，

${\frac {dq_{1}}{dt}}=k_{21}q_{2}-k_{12}q_{1}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{21}q_{2}$.

由于系统中没有示踪剂损失，

$q_{1}+q_{2}={\text{constant}}=q_{0}\,\!$

因此，

${\frac {dq_{1}}{dt}}=-{\frac {dq_{2}}{dt}}\,,$

表明，当隔室#1中示踪剂数量减少时，隔室#2中的数量增加，反之亦然。现在，考虑上图所示的情况，示踪剂在时间 *t* = 0 时注入隔室#1。此时，

$q_{1}=q_{0}\,\!$

以及

$q_{2}=0\,,\,\!$

以及，最初，

${\frac {dq_{1}}{dt}}=-k_{12}q_{0}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{0}$

这些方程的解是

$q_{1}=q_{0}\left\lbrack 1-{\frac {k_{12}}{k_{12}+k_{21}}}\left\lbrace 1-\ {\text{exp}}\ -(k_{12}+k_{21})t\right\rbrace \right\rbrack$

以及

$q_{2}=q_{0}\left\lbrack {\frac {k_{12}}{k_{12}+k_{21}}}\left\lbrace 1-\ {\text{exp}}\ -(k_{12}+k_{21})t\right\rbrace \right\rbrack$

它们在特殊情况下 *k*₁₂ = *k*₂₁ 且两个隔室体积相同时的行为，如下所示

隔室#1 和 #2 中示踪剂数量随时间变化的图形说明。

请注意，该模型预测，当隔室#1 中示踪剂数量呈指数下降，隔室#2 中示踪剂数量呈指数上升时，将达到稳态，每个变化的速率由周转率之和控制。

双隔室模型 - 开放链式系统

这是前面提到的单隔室模型的扩展，它包含两个串联的隔室，如下图所示

开放链式双隔室模型。

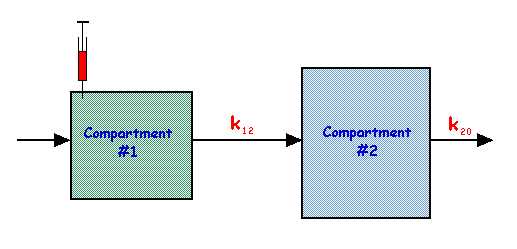
在这个模型中，

${\frac {dq_{1}}{dt}}=-k_{12}q_{1}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{20}q_{2}$

这些方程的解是

$q_{1}=q_{0}\ {\text{exp}}(-k_{12}t)$

以及

$q_{2}=q_{0}{\frac {k_{12}}{k_{12}-k_{20}}}\lbrack {\text{exp}}(-k_{20}t)-{\text{exp}}(-k_{12}t)\rbrack \,,$

并且当 k₂₀ 为 k₁₂ 的三倍时，q₁ 和 q₂ 的行为如下图所示

开放式串联双室模型中示踪剂量随时间的变化图。

请注意，此图中 q₂ 的行为类似于静脉注射后动脉示踪剂的流动，以及放射剂量学中使用的 累积活度 参数。

双室模型 - 开放式乳头系统

该模型等同于上面讨论的封闭式双室系统，但在其中增加了一个从一个室流出的路径。

开放式乳头双室模型。

在这种情况下，

${\frac {dq_{1}}{dt}}=-k_{10}q_{1}-k_{12}q_{1}+k_{21}q_{2}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{1}-k_{21}q_{2}$

当 t = 0 时

$q_{1}=q_{0}\,\!$

以及

$q_{2}=0\,\!$

最初，

${\frac {dq_{1}}{dt}}=-(k_{10}+k_{12})q_{1}$

以及

${\frac {dq_{2}}{dt}}=k_{12}q_{0}$

这些方程的解是

$q_{1}=q_{0}\left\lbrack {\frac {k_{21}-a_{1}}{a_{2}-a_{1}}}{\text{exp}}(-a_{1}t)+{\frac {k_{21}-a_{2}}{a_{1}-a_{2}}}{\text{exp}}(-a_{2}t)\right\rbrack$

以及

$q_{2}={\frac {q_{0}k_{12}}{a_{2}-a_{1}}}\lbrack {\text{exp}}(-a_{1}t)-{\text{exp}}(-a_{2}t)\rbrack$

其中

$a_{1}a_{2}=k_{10}k_{21}\,\!$

以及

$a_{1}+a_{2}=k_{10}+k_{21}+k_{12}\,\!$

q₁ 和 q₂ 的行为在下面的图中说明。

开放性乳头状双室模型中示踪剂数量与时间的图形说明。

该模型已被广泛应用于

• 血浆蛋白 代谢的研究，其中 1 号室代表血浆，2 号室代表血管外空间。
• 锝离子在甲状腺 中的捕获，其中
  • 1 号室：血浆。
  • 2 号室：甲状腺。
  • k₁₂：从血浆到腺体的清除率。
  • k₂₁：从腺体到血浆的泄漏率。

三室模型

上面的开放性乳头状模型已被扩展到使用第三室来研究碘摄取，该室由从 2 号室的不可逆流k₂₃供给。

甲状腺碘摄取模型。

其中

• 1 号室：血浆。
• 2 号室：甲状腺中无机碘的捕获。
• 3 号室：甲状腺内已与激素合成过程中的有机成分结合的碘。

开放性乳头状模型也被应用于肾脏清除率，其中系统由一个血管内室组成，一个血管外室与其交换并与尿液室不可逆地连接。

肾脏清除率模型。

上图中的血管内室（#1）代表可与肾实质和血管外空间交换的示踪剂。尿液室（#2）代表已被肾脏清除的示踪剂，因此与肾盂和膀胱相关。血管外室（#3）代表未被清除的示踪剂，例如与其他分子结合的示踪剂或肾外组织中的示踪剂。

当示踪剂通过周围静脉注入血管内室时，初始分布不会在全身均匀分布 - 但随着血液循环，这种非均匀性会逐渐消失。对于高度血管化的区域，示踪剂数量与时间的曲线将显示出初始的急剧上升，然后迅速下降。此峰值的幅度将随以下因素而变化：

• 解剖区域。
• 注射部位。
• 注射速度。

因此，隔室分析不能应用于肾图的这一阶段，因为隔室分析中隐含的示踪剂均匀分布的基本假设不适用。

在此阶段之后，由于以下原因，血管内室中的示踪剂数量开始下降：

• 被肾脏吸收 - 上图中的k₁₂表示。
• 扩散到血管外空间 - 上图中的k₁₃表示。

随着血管外室中示踪剂数量的增加，反方向的交换开始发生（上图中的k₃₁表示），因此在示踪剂数量下降之前会达到最大值。以下图说明了当

k12 = 0.05 每分钟	k13 = 0.04 每分钟	k31 = 0.06 每分钟
l1 = 0.13 每分钟	l2 = 0.024 每分钟
A1 = 0.65	A2 = 0.35

肾脏清除率模型的预测。

最终，所有示踪剂都将最终进入尿液室。

上面图中使用的方程为

$q_{1}=A_{1}\ {\text{exp}}(-l_{1}t)+A_{2}\ {\text{exp}}(-l_{2}t)\,\!$

$q_{2}=A_{3}\ {\text{exp}}(-l_{1}t)-A_{4}\ {\text{exp}}(-l_{2}t)\,\!$

$q_{3}=A_{5}\ \lbrack {\text{exp}}(-l_{1}t)-A_{2}\ {\text{exp}}(-l_{2}t)\rbrack \,\!$

其中l₁ 和 l₂ 是与分数周转率相关的常数，A₁ 到 A₅ 也是常数，使得

$A_{1}+A_{2}=1\,\!$

以及

$A_{3}+A_{4}=1\,\!$

在实践中，肾清除率可以通过监测血管内区室中示踪剂的量来获得，例如血浆浓度P，其中

$P={\frac {\text{Quantity of Tracer in Intravascular Space}}{\text{Volume of Intravascular Space}}}$

这种血浆浓度的时间依赖性将与q₁的变化方式相同，因此

$P(t)=C_{1}\ {\text{exp}}(-l_{1}t)+C_{2}\ {\text{exp}}(l_{2}t)\,\!$

其中C₁和C₂分别与A₁和A₂相关。因此，肾清除率与k₁₂相关，可以通过表征血管内区室中示踪剂量的双指数衰减来确定。

肾小球滤过率

肾小球滤过率（GFR）通常被认为是肾功能最重要的单一指标之一。它在评估肾衰竭的存在和严重程度方面尤为重要。

有三种主要方法可以确定患者的 GFR

• 菊粉清除率，
• 肌酐清除率，
• 放射性示踪剂清除率。

菊粉清除率已使用多年，通常被认为是三种方法中最可靠和最准确的方法。然而，其主要缺点包括需要持续静脉输注、通过膀胱导管进行定时尿液收集以及漫长的化学分析。肌酐清除率因此已被广泛用于常规 GFR 评估。然而，虽然这种方法在正常情况下与菊粉清除率产生类似的结果，但在中度至晚期肾衰竭患者中其结果的有效性值得怀疑，因为肾小管分泌的意义越来越大。

第三种方法，放射性示踪剂清除率已被广泛采用，使用⁵¹Cr-EDTA。这种示踪剂已知在生理上是惰性的，不与血浆蛋白结合，也不被红细胞或肾脏以外的器官代谢。它通常在注射后 24 小时内排泄，其中 98% 通过肾脏排泄。⁵¹Cr 的半衰期约为 28 天，并通过 100% 的电子俘获衰变为稳定的钒，在大约 10% 的转化中发射单能（320 keV）伽马射线。此外，⁵¹Cr-EDTA 测定的 GFR 可与 OIH 肾血浆流量评估结合使用，用于各种肾脏疾病的鉴别诊断。

⁵¹Cr-EDTA 清除率通常使用的放射性活度为 1-10 MBq，放射性药物通常通过静脉注射给药。这种单次注射技术通过静脉血样评估 GFR，在最简单的情况下，或者通过更复杂的方法连续外部监测⁵¹Cr 中的伽马射线。当患者计数与时间在对数/线性轴上作图时，会生成一条曲线，它最初迅速下降，然后以恒定速率下降，代表q₁在我们最后一张图中的行为。这种初始下降是由于放射性示踪剂与血管外、细胞外液之间的平衡建立所致。较慢的第二阶段反映了肾脏排泄，并包含评估 GFR 所需的信息。

⁵¹Cr-EDTA 的血浆清除率是使用上面讨论的三室模型预测的。

一种快速简便的技术是从患者身上获取两个血样，一个在注射后两小时，另一个在注射后四小时。使用闪烁计数器确定每个样品中血浆中每单位体积的计数，并与标准溶液中的计数进行比较。标准溶液是通过将与患者相同的注射液稀释在已知体积的水中制成的，例如 1 升。

上述曲线第二部分的斜率 m 可以由以下公式确定

$m={\frac {\ln b_{1}-\ln b_{2}}{t_{2}-t_{1}}}$

其中

• t₁：第一个血样注射后的时间，通常为 120 分钟，
• b₁：第一个血样血浆中的计数/毫升（mL）（已校正背景计数），
• t₂：第二个血样注射后的时间，通常为 240 分钟，
• b₂：第二个血样血浆中的计数/mL（也已校正背景）。

现在，我们可以将这条直线外推到注射时间t₀，以确定示踪剂在患者血浆区室中瞬时混合时的血浆计数，即

$\ln b_{0}=\ln b_{1}+m(t_{1}-t_{0})\,\!$

如下图所示

两个血浆样品的计数拟合到一条直线，这条直线外推到注射时间（虚线），以确定 b₀ 的对数。使用三室模型预测的血浆清除率 q₁ 以阴影显示。

因此，我们可以写

$b_{0}={\text{exp}}\ {\big (}\ln b_{1}+m(t_{1}-t_{0}){\big )}$

现在可以使用**稀释原理**通过比较血浆计数和标准溶液的计数来确定该血浆隔室的体积，即

$V={\frac {S\cdot V_{s}}{b_{0}}}$

这导致

$V={\frac {S\cdot 1000}{b_{0}}}$

当标准注射稀释在 1 升中时。然后用以下公式给出清除率（以毫升/分钟表示）

${\text{Clearance}}=V\cdot m\,\!$

下面显示了两个患者的结果，以说明此技术。

患者 A

样本	计数/毫升
背景	477
b1 在 119 分钟	11,438
b2 在 238 分钟	6,235
标准，S	150,020

该患者的⁵¹Cr-EDTA 清除率被确定为 38.8 毫升/分钟。评估结果表明慢性肾功能衰竭，后来发现是由于狼疮性肾炎引起的。随后患者接受了类固醇治疗。

两个月后，患者再次接受检测，发现清除率升至 52.7 毫升/分钟。对于患者的年龄，该清除率被认为在正常范围内，表明治疗正在产生积极效果。然后停止治疗。两个月后，患者再次接受检测，在此期间未接受类固醇治疗。结果为 54.2 毫升/分钟，反映出治疗成功。

患者 B

样本	计数/毫升
背景	425
b1 在 122 分钟	3,103
b2 在 250 分钟	1,390
标准，S	104,600

该患者血压高，需要确认肾脏受累情况。然而，清除率为 117.3 毫升/分钟，远在正常范围内。因此，排除了肾脏对该患者疾病的调查。

---

请注意，血液样本数量不限于两个，有些方法需要三个、四个或更多样本，而其他方法使用外部监测清除率。然而，每种方法都基于上述分析形式，其中确定清除曲线第二阶段的速率常数以及放射性示踪剂的分布体积。因此，血液采样时间是在第一阶段结束后，即注射后超过约两个小时，使用单指数拟合到此后阶段来确定分布体积。

---

重要的是要理解，如上所述确定的⁵¹Cr-EDTA 清除率并不直接等同于肾小球滤过率 (GFR)，因为该方法假设单指数依赖性。因此，⁵¹Cr-EDTA 清除率结果通常通过经验或理论推导的因子进行校正，以迫使它们表示真实的 GFR。经验校正包括

• Chantler (1969)，其中⁵¹Cr-EDTA 清除率乘以 0.8 的因子；
• Brien (1969)，其中大于 50 毫升/分钟的清除率乘以 0.82 并加上 6；
• Brochner-Mortensen (1972)，其中应用二阶多项式

获得 GFR。基于隔室分析的真实 GFR 与单指数清除率值之间关系的理论考虑的校正已引入(Fleming, 2007)，它提供了改进的校正，特别是在高 GFR 时。此校正的形式为

$GFR={\frac {\text{Clearance}}{(1+f\cdot {\text{Clearance}})}}$

其中 $f$ = 0.0017 分钟/毫升。

作为最后一步，校正后的清除率测量通常标准化为标准人的体表面积 (BSA)，即 1.73 平方米。这通常是使用基于患者身高和体重的 BSA 估计值来完成的 - 例如，来自DuBois (1916)或Haycock (1978)。还引入了基于 BSA 缩放清除率的单指数校正技术 (Jodal & Brochner-Mortensen, 2008)，它类似于 Fleming (2007) 的方法，但在儿科研究中提供了改进的校正。

肾图

从上面的讨论中应该清楚，尿液隔室（＃2）包含尿液中示踪剂的数量，而不区分尿液是在肾盂、输尿管还是膀胱中。可以通过将三隔室乳头模型扩展到五个隔室来合并这些解剖空间

应用于肾图的隔室分析。

请注意，示踪剂通过肾实质的通过可以用转运时间t₀来表征，并且k₅₆与尿液生成率相关。

肾实质、肾盂和膀胱中示踪剂数量的最终微分方程的解包含对时间延迟t₀的考虑，因此

• 当t < t₀

${\color {Blue}q_{4}=1-A_{3}\ {\text{exp}}(-l_{1}t)-A_{4}\ {\text{exp}}(-l_{2}t)}\,\!$

${\color {Red}q_{5}=0}\,\!$

${\color {OliveGreen}q_{6}=0}\,\!$

• 当 t > t₀

${\color {Blue}q_{4}=A_{3}[1-{\text{exp}}(-l_{1}t_{0})]{\text{exp}}(-l_{1}\lbrace t-t_{0}\rbrace )+A_{4}[1-{\text{exp}}(-l_{2}t_{0})]{\text{exp}}(-l_{2}\lbrace t-t_{0}\rbrace )}\,\!$

${\color {Red}q_{5}=A_{7}\ {\text{exp}}(-l_{1}\lbrace t-t_{0}\rbrace )+A_{8}\ {\text{exp}}(-l_{2}\lbrace t-t_{0}\rbrace )-A_{9}\ {\text{exp}}(-l_{3}\lbrace t-t_{0}\rbrace )}\,\!$

${\color {OliveGreen}q_{6}=1-A_{10}\ {\text{exp}}(-l_{1}\lbrace t-t_{0}\rbrace )-A_{11}\ {\text{exp}}(-l_{2}\lbrace t-t_{0}\rbrace )+A_{12}\ {\text{exp}}(-l_{3}\lbrace t-t_{0}\rbrace )}\,\!$

其中 l₃ 与 k₅₆ 相关。每个隔室中示踪剂数量的时间过程如下图所示

使用 t₀ = 2 分钟和 k₅₆ = 1 每分钟生成的肾实质 (q₄)、肾盂 (q₅) 和膀胱 (q₆) 曲线。

可以通过将肾实质和肾盂曲线相加来获得整个肾脏中示踪剂的数量，因此

$q_{\text{kidney}}=q_{4}+q_{5}\,\!$

如下图所示

肾盂和实质曲线相加的结果。

在实践中，肾图记录的不仅仅是肾脏曲线，还有示踪剂在

• 重叠和底层组织，以及
• 肾脏本身的血管内空间。

这些贡献叠加了真实的肾图，形成了一个 **背景**。背景中示踪剂的数量随时间变化，但与真实的肾脏曲线变化方式不同。该背景的时间过程可能与前面使用五隔室模型得出的血管内 (q₁) 和血管外 (q₃) 曲线的总和类似。

在此基础上，可以推导出以下公式

$q_{\text{Bgd}}=b_{1}q_{1}+b_{3}q_{3}\,\!$

其中 b₁ 和 b₃ 分别代表血管内和血管外空间中示踪剂对检测到的肾图曲线的贡献。例如，下面的曲线使用 b₁ = 0.05 和 b₃ = 0.02 生成，以及

$q_{\text{Renogram}}=0.5\,q_{\text{Kidney}}+q_{\text{Bgd}}\,\!$

实际中获得的肾图和背景曲线典型示例。

实际上，应该从原始肾图数据中减去此背景曲线，以获得反映肾脏中示踪剂真实量的曲线（见前图）。此过程有时被称为 **血液背景扣除**——虽然你现在应该能够理解，这是一个有点错误的说法！

下面显示了未校正和校正后的曲线，以帮助直接比较。

肾图曲线在背景校正前后。

以及患者 ^99mTc-DTPA 肾图的示例，如下所示，以帮助您将其与室模型分析的预测结果进行比较。

最后一张图说明了一种可用于 ^99mTc-MAG3 肾图的分析方法，适用于患有梗阻性泌尿道病的患者。

MAG3 肾图分析。

肾图中的背景扣除

在实践中，在解释肾图时必须考虑肾图中的背景活性。这通常通过估计背景活性并将其从原始肾图数据中减去来实现。问题是：如何测量这种背景活性？

一种方法是基于记录患者肾切除部位的活性，这些患者的剩余肾脏正在接受检查。但是，应该注意的是，切除肾脏也会去除背景活性的血管内来源。因此，肾切除部位在肾图图像中通常比肾外组织更冷。

一种潜在的更好方法是记录非功能性肾脏区域的活性。

然而，在大多数患者中，必须使用非肾脏区域来估计背景。理想情况下，区域的选择应该反映与肾脏本身相同的血管内和血管外背景。在这个领域似乎没有标准化，实践包括使用肾脏之间的区域、肾脏上方、心脏上方以及每个肾脏下方。

Taylor 等人 (1997) 提供了此类方法的比较，并且类似但更基本分析的结果总结如下。

Bgd RoI 位置

这些肾图图像使用蒙特卡洛模拟 生成，并使用 OsiriX 分析。分裂函数使用 90-150 秒时间段内的计数积分计算。平均绝对百分比误差是从一系列此类模拟图像中计算得出的，其中左肾与右肾的分裂函数从 100%:0% 到 50%:50% 再到 0%:100%，步长为 5%。

可以看出，侧向 RoI 产生的百分比误差最低，而中心 RoI（在早期使用 ^99mTc-DTPA 进行伽马相机肾图时使用）产生的误差明显更大，约为 12%。这与目前的临床实践一致，在目前的临床实践中，不再使用中心 RoI，而更倾向于使用侧向或倾斜的 RoI，或肾周 RoI。

相比之下，没有背景校正会产生 20.7% 的误差，这突出了背景校正的整体重要性。

对于真实的 LK:RK 分裂函数比率 50%:50% 以及 100%:0% 和 0%:100% 的极值，背景活性的变化如下图所示。

侧向背景数据的 6 次多项式拟合。

使用 32 帧平均值在时间上平滑的蒙特卡洛模拟 AP 肾图。原始数据由 dynamicrenalstudy.org 提供。

首先要注意的是，背景曲线随时间的变化方式反映了肾脏曲线本身，在摄取阶段迅速上升，在排泄阶段缓慢下降。其次，请注意，右肾 (RK) 曲线下降速度比左肾 (LK) 曲线慢——这可能是由于 MAG3 示踪剂在肝脏中滞留造成的。这与 之前 分析模型中使用的假设完全不同。从左侧的蒙特卡洛模拟 AP 肾图 可以看出肝脏参与的程度，其中可以观察到整个研究过程中肝脏及其动态的合理视图。这与用于生成虚拟研究的药代动力学模型 一致。

第三，请注意，在 50%:50% 和 0%:100% 时，RK 曲线比 LK 曲线幅度更大，而在 100%:0% 时则相反。这突出了需要对每个肾脏使用单独的背景 RoI。

最后一点需要注意的是，与 90-150 秒的时间窗口有关，在该窗口中通常应用 积分或斜率方法。可以看出，背景计数的总和（**积分**）和这些计数的变化率（**斜率**）在此期间都在变化，这表明这两种方法都会受到背景曲线这些特征的影响。

选择好背景区域并生成活性/时间曲线后，应该将背景曲线按一个取决于背景区域和肾脏区域的相对面积的因子进行缩放，然后将其从原始肾图曲线中减去。此外，请注意，一些实践还包括根据肾脏位置进一步缩放背景曲线。最后，开发了更复杂的方法来进行背景校正，包括

• 根据肾脏周围的背景样本生成插值背景区域，
• 使用外推技术估计背景校正因子，以及
• 反卷积分析。.

需要注意的是，在将这些结果直接转化为真实患者研究时应谨慎，因为原始数据来自室模型的二维表示。

相对肾功能

患者肾脏的相对功能通常定义为该肾脏的肾脏清除率，以患者总肾脏清除率的百分比表示，即

${\text{LK Relative Fn.}}={\frac {\text{LK Clearance}}{{\text{LK}}+{\text{RK Clearance}}}}$

以及

${\text{RK Relative Fn.}}={\frac {\text{RK Clearance}}{{\text{LK}}+{\text{RK Clearance}}}}$

其中 LK 和 RK 分别代表左肾和右肾。

假设

• N_Kidney(t)：背景校正后的肾脏计数率，以及

• N_Bgd(t)：来自血管内感兴趣区域的计数率。

此时应该很明显

$N_{\text{Kidney}}(t)\ \alpha \ q_{4}(t)\,\!$

以及

$N_{\text{Bgd}}\ \alpha \ q_{1}(t)\,\!$

因此，我们可以得出结论，在肾图的初始阶段，即当 t < t₀ 时

$N_{\text{Kidney}}(t)=UC\int _{0}^{t}N_{\text{Bgd}}(t)\cdot dt$

其中 UC 是肾脏摄取常数。此常数与该肾脏的清除率相关，因此我们可以写成

${\text{LK Relative Fn.}}={\frac {\text{LK Update Constant}}{{\text{LK}}+{\text{RK Uptake Constant}}}}$

以及

${\text{RK Relative Fn.}}={\frac {\text{RK Uptake Constant}}{{\text{LK}}+{\text{RK Uptake Constant}}}}$

然而，我们已经从上面看到背景校正后的肾脏计数率与摄取常数直接相关，因此我们可以得出结论

${\text{LK Relative Fn.}}={\frac {\text{LK Counts}}{{\text{LK}}+{\text{RK Counts}}}}$

以及

${\text{RK Relative Fn.}}={\frac {\text{RK Counts}}{{\text{LK}}+{\text{RK Counts}}}}$

请注意，此分析表明，可以通过测量初始血管峰值后但在排泄阶段开始之前每个肾脏中的相对计数来确定相对肾脏功能。

肾脏深度校正

鉴于两个肾脏可以在患者体内处于不同的深度，通常会对光子衰减的差异进行校正。传统的方法是在进行肾图后获取侧视图，以测量每个肾脏的深度，并基于假定的伽马射线能量线性衰减系数（例如，^99mTc 伽马射线为 0.153 cm^-1）进行指数校正。

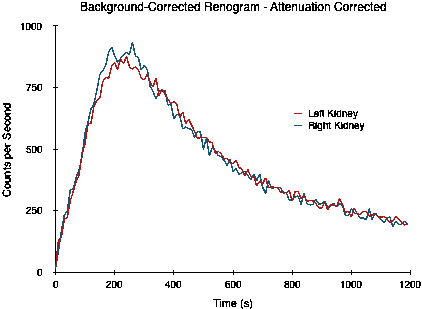
以下研究说明了这种情况，其中右肾比左肾深约 1 厘米。该研究实际上是通过蒙特卡罗模拟数字体模 (XCAT) 生成的图像，其中包括光子衰减、散射、有限空间分辨率和噪声的影响。左肾的位置深度为 7.31 厘米，而右肾的深度为 8.64 厘米，分割功能为 50:50。

[[File:nm14 301e.gif|thumb|center|A virtual renogram acquired at 10 seconds per frame for 120 frames. Raw data courtesy of dynamicrenalstudy.org|alt=A virtual renogram.

用于肾图分析的感兴趣区域。

请注意，由于衰减的差异，两条曲线并没有重叠，而这在 50:50 分割功能中是预期的。通过 90 到 150 秒之间的计数积分估计的分割功能为 54:46。然而，当校正这种衰减差异时，将获得以下曲线，并且分割功能估计现在更接近实际的 49:51。

虚拟肾图，衰减校正。

商业肾脏分析软件通常提供基于患者身高和体重与每个肾脏深度之间经验得出的关系自动计算肾脏深度的选项。其中一个软件包提供了以下选项（体重以公斤表示，身高以厘米表示）

方法	左肾深度 (cm)	右肾深度 (cm)
标准	13.2*(体重/身高)+0.7	13.3*(体重/身高)+0.7
埃默里	16.17*(体重/身高)+0.027*年龄（年） - 0.94	15.13*(体重/身高)+0.022*年龄（年） + 0.077 注意：包含印刷错误
伊藤	14.0285*(体重/身高)0.7554	13.6361*(体重/身高)0.6996
T. 伊藤	17.05*(体重/身高) + 0.13	16.55*(体重/身高) + 0.66

下图显示了这些方程在广泛的体重身高比范围内生成的肾脏深度差异的图形表示（注意：埃默里公式假定了 50 岁的年龄）

肾脏深度差异（左肾深度减去右肾深度）。

可以看出，标准公式预测的深度变化很小，因此派生的衰减校正可能对相对功能估计的影响很小。还可以看出，T. 伊藤公式表明右肾始终比左肾更深。后两组公式表明，对于体重身高比小于 0.6 到 0.7 的情况，右肾更深，而在该范围之上，左肾更深。可以看出，这后三组公式预测的总体深度差异范围不超过 ±5 毫米。这种差异产生的预期衰减校正因子在 0.95 到 1.05 的范围内。

应将这些公式的预测与肾脏深度研究的结果进行对比，研究结果表明，在约 60% 的患者中可以预期大于 5 毫米的差异，而在约三分之一的患者中可以预期大于 1 厘米的差异。因此可以推断，上述公式仅在不到一半的患者中提供足够的衰减校正，并且偶尔可以预期衰减校正因子低至 0.6。

因此，显而易见的是，准确的肾脏深度测量对于正确解释所有肾图至关重要，并且应谨慎使用自动肾脏深度公式。

^99mTc-MAG3 肾图分析的半自动方法

肾图分析的商业软件通常提供多种所谓的半自动分析方法——其中一些分析功能需要用户交互（例如肾脏识别），而其他功能则自动执行（例如计算），以确定肾脏分割功能和有效肾血浆流量 (ERPF)。在此，软件可能会要求用户例如

• 输入患者的身高和体重——以便使用经验得出的公式计算体表面积和肾脏深度，以及
• 在每个肾脏周围定义感兴趣区域 (RoI)——并自动在这些肾脏 RoI 旁边放置背景区域。

为这四个 RoI 生成计数/时间曲线。然后自动将背景 RoI 中的计数按比例缩放到与相应肾脏 RoI 大小相同的背景区域的计数，并将缩放后的背景曲线从肾脏曲线中减去，以生成每个肾脏的净肾图曲线。

然后使用每个肾图中预定义时间间隔内（例如注射后 1 到 2 分钟）的计数来计算

• 计数的总和（称为积分）和/或
• 计数的增加速率（称为斜率）

每个肾脏。

使用前面使用的肾图系列的侧向 RoI 进行背景减法，并使用 90 到 150 秒的时间段进行分析，对这两种方法进行了比较。两种方法都产生了非常相似的结果

然而，积分方法产生的平均绝对百分比误差仅为 2.6%，而斜率方法产生的误差明显更大，为 9.4%——主要原因是 LK/RK 比率较低和较高时的精度不足。

相比之下，使用积分法时，没有进行背景校正会导致 20.7% 的误差，而使用斜率法时，误差仅为 9.2%。这再次强调了此类校正的重要性。

可以使用每个肾脏的计算深度和假定的^99mTc伽马射线的线性衰减系数来校正积分以消除组织衰减。以这种方式计算积分是这种分析方法的主要误差来源，因为使用患者的身高和体重（以及某些方法中的年龄）来确定肾脏深度可能会不准确 - 请参阅上一节。此外，肾脏显像扫描情况下的线性衰减系数 (μ) 值没有标准，临床使用值如 0.12、0.14 和 0.153 每厘米。例如，对于 6 厘米的肾脏深度，这些 μ 值会导致应用 2 到 2.5 之间的校正因子，即给出约 20% 的变化。

分割函数可以通过每个肾脏的衰减校正 (AC) 积分对两个肾脏的 AC 积分之和的百分比贡献来确定。

此外，肾脏摄取可以通过将 AC 积分表示为注射剂量的百分比来确定。

有效肾脏血浆流量 (ERPF) 然后可以根据经验推导的公式计算，例如

左肾 ERPF (毫升/分钟) = -21.579 + (11.621 * 左肾摄取)

以及

ERPF 值 (毫升/分钟) = 14.98 * (左肾摄取 + 右肾摄取) + 8.28

或者，可以将洗脱系数定义为

0.48026*(exp(1.35315*肾脏摄取总和)/100)-1

乘以血浆体积估计值，例如

体表面积 * 1,000 + 0.608 毫升

得到总 MAG3 清除率。此最终因子用于使用以下公式计算总 ERPF (毫升/分钟)

1.25821* (总 MAG3 清除率) + 18.34451

0.53 也被用作 ERPF 转换因子，即从 ERPF 转换为 MAG3 清除率。但是，需要注意的是，该因子的值在 0.61 到 0.9 之间。

作为这些基于积分的方法的替代方案，肾脏曲线在肾脏显像的摄取阶段的斜率已被用来定义每个肾脏的斜率指数，该指数基于每个肾脏显像的斜率，针对肾脏深度进行衰减校正，并表示为注射剂量的百分比乘以 10⁶! 然后可以推测通过将每个肾脏的斜率指数与斜率指数之和相关联来获得分割函数 - 并使用以下公式计算总 MAG3 清除率

(12.725 * 肾脏斜率指数之和 + 6.24)/体表面积

体表面积 (BSA) 估算也是这些计算中变化的另一个来源。它被广泛用于将患者的 ERPF 参考到标准 BSA，例如 1.73 平方米。它也用于使用上述公式等公式进行计算。该领域至少使用两种 BSA 计算方法，如下所述

Du Bois 公式：BSA = 0.007184 * W^0.425 * H^0.725

以及

Haycock 公式：BSA = 0.024265 * W^0.5378 * H^0.3964

其中 W 是患者的体重（公斤），H 是身高（厘米），BSA 以平方米表示。对于成人来说，这些公式给出了相当相似的 BSA 估计值，例如，对于体重为 69 公斤，身高为 163 厘米的患者，两者之间的差异约为 2%，因此在这种应用中，它们的选择结果并不重要，无论它们是否准确。

总之，商业半自动肾脏分析软件通常基于以下两种方法之一

• 确定每个肾脏的 MAG3 的绝对摄取量，并将这些摄取量与从有限患者研究中得出的经验关系联系起来（例如，在 Itoh 等人的情况下，可能是 36 名假设是日本人的患者））
• 确定每个肾脏的 MAG3 摄取率，并将这些摄取率与从有限患者研究中得出的经验关系联系起来（例如，在 Oriuchi 等人的情况下，可能是 12 名假设是日本人的患者））。

鉴于显而易见的强经验特征和调查的患者数量非常有限，有必要评估这些方法的准确性。可以使用蒙特卡洛模拟肾脏显像 进行此类评估，下表显示了此类评估的结果

使用两种不同商业软件包对六个虚拟肾脏显像的五种不同分析方法估算的 MAG3 清除率和分割函数的比较。

对于此评估，Itoh ERPF (MAG3)、Inoue (无样本 MAG3) 和 Oriuchi 清除率 (MAG3) 方法的公式 用于使用电子表格软件计算每个肾脏显像的 MAG3 清除率和分割函数。使用制造商的软件包直接计算 ERPF 修正 Schlegel 和 ERPF 修正 Gates 方法的这些参数值，并假设 ERPF 转换因子为 0.76（即 Oriuchi 研究的平均值） - Itoh 方法也是如此。

很明显，所有结果中都没有相关性，例如，当 MAG3 清除率从 260 毫升/分钟减半到 130 毫升/分钟时，计算出的清除率也会降低 - 尽管在某些情况下，修正 Schlegel 方法的结果相当合理。第二个要点是，分割函数估计的变化可能部分是由于使用了（可能是不准确的）自动肾脏深度确定方法。

那么......这些自动计算是否应该在没有例如来自横断扫描、肾脏显像后或超声扫描的肾脏深度测量结果的确认的情况下进行临床应用？这个问题在 1985 年得到了解答，但不幸的是，这个问题似乎还没有渗透到现代肾脏分析软件生产商的心理。

另一个问题：商业双头伽马相机软件包是否应该考虑将共轭成像用于肾脏显像分析？

肾脏显像中的共轭成像

共轭成像的原理基于计算来自两个相对探测器的活性测量的几何平均值，并在以下图表中说明，其中一个均匀介质（黄色矩形）包含一个放射性点源（红色点）。介质的厚度为 d，点源距离探测器 #1 为 t₁，距离探测器 #2 为 t₂。

共轭计数。

假设没有检测到散射，探测器 #1 检测到的活性由下式给出

$A_{1}=A\exp(-\mu *t_{1})$

而探测器 #2 检测到的活性由下式给出

$A_{2}=A\exp(-\mu *t_{2})$.

检测到的活性的几何平均值 GM 由下式给出

$GM={\sqrt {A_{1}*A_{2}}}$

以便

$GM={\sqrt {A\exp(-\mu *t_{1})*A\exp(-\mu *t_{2})}}$

因此

$GM={\sqrt {A\exp(-\mu *t_{1})*A\exp(-\mu *(d-t_{1}))}}$

因此

$GM={\sqrt {A\exp(-\mu *d)}}$

该最终方程表明几何平均值仅取决于介质厚度 d，该介质包含点源，而不依赖于源到任一探测器的距离。

将此翻译成肾图术意味着使用相对的伽马相机头成像（如双相机 SPECT 系统）将提供独立于肾脏深度的分离功能测量值。

肾图术中的共轭成像由以下蒙特卡罗模拟肾图图像说明，这些图像使用前后（AP）和后前（PA）投影同时获取。模拟的肾脏深度左侧为 7.31 厘米，右侧为 8.64 厘米，真实的 LK/RK 分离功能比率为 50%：50%。

左侧为前后（AP），右侧为后前（PA）蒙特卡罗模拟肾图。原始数据由 dynamicrenalstudy.org 提供。

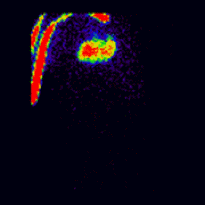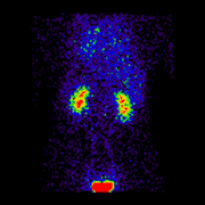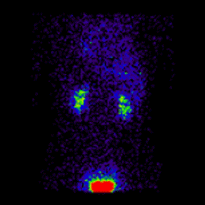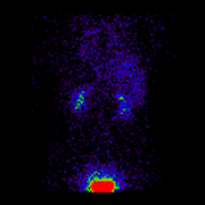
几何平均肾图

几何平均肾图的曲线。

这些图像用于使用 ImageJ 计算几何平均值，并使用 OsiriX 分析所得图像。图像计算涉及将 AP 和 PA 肾图相乘，并以 32 位精度取结果的平方根。计算后的图像被转换为 16 位以进行 DICOM 存储。所得几何平均肾图（见上面的中心面板）提供了 LK/RK 分离功能估计值为 51%：49%，而未校正肾脏深度的仅 PA 数据提供了较差的估计值为 54%：46%。

从上面的说明可以看出，共轭成像在临床肾图术中可能发挥作用，并且可能不依赖于肾脏深度测量进行衰减校正。但是，应该注意的是，该方法假设活动位于具有空间均匀线性衰减系数 μ 的均匀介质中，这表明该方法在真实患者中可能会受到来自诸如覆盖肾脏的消化气体等来源的像差的影响。

作为总结，应该注意的是，共轭计数在使用静态 ^99mTc-DMSA 图像进行定量肾脏分析中已得到充分确立。

血液池补偿用于分离功能测定

最近的一篇出版物介绍了血液池补偿技术，用于在肾图术中确定分离功能。这里，在肾图的摄取阶段，会随时间测量每个肾脏和肝脏的活动。假设肝脏活动代表肾图摄取阶段的血液池活动。然后，对肝脏活动与肾脏活动图的线性拟合进行反外推，使其回到零肝脏活动，以确定零血液池贡献的肾脏活动。然后使用该零活动时的相对贡献来计算分离功能。

以下图形说明了这种简单的方法。在左上角面板中显示了为肝脏、左肾脏和右肾脏定义的三个感兴趣区域 (ROI)，表中的右上角面板显示了三个所得曲线，用于具有 50/50 分离功能的蒙特卡罗模拟肾图。在左下角面板中显示了摄取阶段的肝脏计数与肾脏计数图，其中左肾脏的截距为 17,281 计数，右肾脏的截距为 18,719 计数。然后估计分离功能，左侧为 48%，右侧为 52%。

右下角面板显示了平均绝对 % 误差，该误差从一系列此类模拟图像中计算得出，其中左肾脏与右肾脏的分离功能从 100%：0% 开始，以 5% 的步长递增至 50%：50% 再到 0%：100%，结果为 7.5%。