电路理论/相量/示例/示例 9

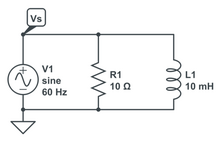
用于示例 9的并联 RL 电路

假设电压源由 $V_{s}(t)=120{\sqrt {2}}cos(377t+120^{\circ })$定义，求出所有其他电压、电流并检查功率。

标记回路和节点

用于分析的标记并联 RL 电路

在并联电路中，所有器件的电压都相同。

已知量、未知量和方程

已知量：$V_{s},R,L$

未知量：$I_{s},i_{R},i_{L}$

方程：$V_{s}(t)=R*i_{R}(t),V_{s}=L*{d \over dt}i_{L}(t),i_{R}(t)+i_{L}(t)-I_{s}(t)=0$

初始条件

在这个问题中，假设初始条件为零是不可能的。

查看端子关系

$V_{s}=V_{L}=L*{d \over dt}i_{L}(t)$

V_S 在 t=0₊ 时具有非零值。这意味着 ${d \over dt}i_{L}(t)=V_{s}/L$。这就是一个初始条件。另一个初始条件是 i_L(0₊) = 0。

微积分符号表示

按以下顺序评估端子关系

$i_{R}(t)={\frac {V_{s}}{R}}$

$i_{L}(t)=\int {\frac {V_{s}}{L}}dt$

$i_{s}(t)=i_{R}(t)+i_{L}(t)$

微积分数值

RL 电路的相量 MATLAB 解法 .... m 文件

$V_{s}(t)=120{\sqrt {2}}\cos(377t+2.09)$

$R=10$

$L=.01$

$i_{R}=12{\sqrt {2}}\cos(377t+2.09)$

$i_{L}=\int {\frac {120{\sqrt {2}}\cos(377t+2.09)}{.01}}dt=45\sin(377t+2.09)+C_{1}$

$i_{L}(0)=0=45\sin(2.09)+C_{1}$

$C_{1}=-39$

$i_{L}=45\sin(377t+2.09)-39$

$I_{s}(t)=12{\sqrt {2}}\cos(377t+2.09)+45\sin(377t+2.09)-39$

相量数学避免使用三角函数！ m 文件

下一步是将答案组合成一个具有相移的余弦项，以便它可以与 $i_{L}$ 和 $i_{R}$ 进行比较。-39 变成了直流偏置。

组合正弦项和余弦项的最简单方法是相量。

以下是相量方法。注意数学是在相量域中完成的...使用虚数。

$12*{\sqrt {2}}*(377t+2.09)\Leftrightarrow 12*{\sqrt {2}}cos(2.09)+j12*{\sqrt {2}}sin(2.09)$

$45sin(377t+2.09)\Leftrightarrow 45*sin(2.09)-j45*cos(2.09)$

现在数字在相量世界中。下一步是将它们全部加起来。

$\mathbb {I} _{s}=48.1\angle 0.884$

现在将结果转换回时域。

$I_{s}=48.1\cos(377t+0.884)-39$

相量符号

时域

$i_{R}=V_{s}/R$

$i_{L}=\int {\frac {V_{s}}{L}}dt$

$i_{S}=i_{R}+i_{L}$

相量域

$V_{s}(t)\rightarrow \mathbb {V}$

$\mathbb {V} =V_{m}\angle \phi$

$\mathbb {I} _{R}={\frac {\mathbb {V} }{R}}={\frac {V_{m}}{R}}\angle \phi$

$\int V_{s}(t)dt\rightarrow {\frac {\mathbb {V} }{j\omega }}={\frac {\mathbb {V} }{\omega }}\angle {\frac {-\pi }{2}}={\frac {V_{m}}{\omega }}\angle (\phi -{\frac {\pi }{2}})$

$\mathbb {I} _{L}={\frac {V_{m}}{\omega L}}\angle (\phi -{\frac {\pi }{2}})$

$\mathbb {I} _{S}={\frac {V_{m}}{R}}\angle \phi +{\frac {V_{m}}{\omega L}}\angle (\phi -{\frac {\pi }{2}})$

$\mathbb {I} _{S}=V_{m}*{\sqrt {{\frac {1}{R^{2}}}+{\frac {1}{(L\omega )^{2}}}}}\angle (\phi -arctan({\frac {R}{L\omega }}))$

回到时域

$I_{L}(t)=\operatorname {Re} (\mathbb {I} _{L}e^{j\omega t})={\frac {V_{m}}{\omega L}}*cos(\omega t+\phi -{\frac {\pi }{2}})+C_{1}$

$I_{s}(t)=\operatorname {Re} (\mathbb {I} _{s}e^{j\omega t})=V_{m}{\sqrt {{\frac {1}{R^{2}}}+{\frac {1}{(L\omega )^{2}}}}}cos(\omega t+\phi -arctan({\frac {R}{L\omega }}))+C_{1}$

$I_{R}(t)=\operatorname {Re} (\mathbb {I} _{R}e^{j\omega t})={\frac {V_{m}}{R}}cos(\omega t+\phi )$

$I_{L}$ 涉及了相量域中的积分，因此在其时域方程中添加了一个常数。

使用相量而不是微积分来解决问题 m-filec

相量数值

如果像上面那样可以用符号形式求解，那么在相量域中进行数学运算就没有意义了。

时域

$i_{r}(t)={\frac {120*{\sqrt {2}}}{10}}\cos(377t+2.09)=17.0cos(377t+2.09)$

$i_{L}(t)={\frac {120*{\sqrt {2}}}{.01*377}}\cos(377t+2.09-{\frac {\pi }{2}})+C_{2}=45\cos(377t+0.524)+C_{1}$

$0=45\cos(0.524)+C_{1}$

$C_{1}=-39.0$

$i_{s}(t)=120*{\sqrt {2}}*{\sqrt {{\frac {1}{10^{2}}}+{\frac {1}{(.01*377)^{2}}}}}\cos(377t+{\frac {2*\phi }{3}}-\arctan({\frac {10}{.01*377}}))-39$

$i_{s}(t)=48.1\cos(377t+0.844)-39$

这些数字与上面用微积分计算的结果相同...

仿真

$Vs$, $I_{s}$, $i_{L}$, 以及 $i_{R}$ 来自仿真的 仿真 在下面绘制。

circuitlab.com 仿真，电流流入一个产生 180° 相移的器件

符号	颜色	方程式
$I_{s}$	棕色	$48.1\cos(377t+50.6^{\circ })-39$
$i_{L}$	橙色	$45\cos(377t+30^{\circ })-39$
$i_{R}$	示例	$17\cos(377t+120^{\circ })$
Vs</math>	蓝色	$170\cos(377t+120^{\circ })$

显示当 circuitlab 跳过 initial=no 时会发生什么...

仿真与数学结果一致。Circuitlab 仿真需要取源电流才能获得正确的相位。这可以通过使用一个正弦波源跨接一个电阻器来测试 circuitlab 来观察。

仿真还表明积分常数取决于源的相位角。

周期检查

上面的周期看起来在 16ms 和 17ms 之间，更接近 17ms。这与公式一致

$\omega =2\pi *f$

$f={\frac {\omega }{2\pi }}$

$T={\frac {1}{f}}={\frac {2\pi }{\omega }}={\frac {2\pi }{377}}=16.7ms$

幅值检查

如果测量峰峰值，仿真幅值与数值答案的双倍幅值相匹配。积分常数添加了一个直流偏置，在本例中为负。

相位检查

无论电流源还是电压源驱动电路，电压始终会领先于电感器中的电流（想想端子关系或 ELI）$90^{\circ },{\frac {\pi }{2}}$ 或 ${\frac {1}{4}}$ 周期。

功率分析

这些常数将在此分析中添加一些直流功率或有功功率。在不知道它们是什么的情况下，我们无法计算它们的影响。因此，现在我们坚持使用相量域功率分析

$\mathbb {V} _{s}=120{\sqrt {2}}\angle 2.09$

$\mathbb {I} _{s}=48.1\angle 0.884$

$\mathbb {I} _{s}^{*}=48.1{\sqrt {2}}\angle -0.884$

如果 :$\mathbb {V} =M_{v}\angle \phi _{v}\quad$，以及 $\quad \mathbb {I} =M_{i}\angle \phi _{i}$，那么

$\mathbb {S} =\mathbb {V} \mathbb {I} ^{*}={\frac {M_{v}M_{i}}{2}}\angle (\phi _{v}-\phi _{i})={\frac {120{\sqrt {2}}*48.1}{2}}\angle (2.09-0.884)=4081\angle 1.206=1456+3813j$

并且

$cos(1.206)=.357$

这是一个很差的功率因数。公用事业的视在功率远远大于客户愿意支付的功率。如上所述的纯感性负载在大型电机中很常见工业环境，在那里工业工程师正在与电力公司工程师进行交流。可能需要功率调节器才能将该功率因数恢复到更接近 1 的水平。公用事业公司将根据视在功率收费……这对他们来说是真正的 $$$。

值	单位	描述
$4081$	伏安 va	视在功率是电力公司管理的内容：他们设计的峰值功率，他们必须提供的峰值功率
$.357$	无量纲	功率因数，有功功率与视在功率的比值，理想情况下为1
$1456$	瓦 W	有功功率、平均功率、有效功率... 消费者想要支付的功率（瓦特小时）
$3813$	无功功率 var	无功功率... 为什么房间里的所有插座不能在同一个断路器上

直觉

ELI... 电压超前于电感器中的电流

积分常数很重要。初始条件很重要。相量不处理这些。

连接到电源的纯感性负载会产生不良的功率因数。

如果积分常数出现，并且没有微分方程，则必须使用初始条件计算积分常数。

电源的相角影响积分常数。