数据结构/简介

数据结构
简介 - 渐进符号 - 数组 - 列表结构和迭代器
 栈和队列 - 树 - 最小堆和最大堆 - 图
 哈希表 - 集合 - 权衡

计算机可以存储和处理大量数据。正式的数据结构使程序员能够将大量数据在概念上组织成易于管理的关系。

有时我们使用数据结构来让我们做更多的事情：例如，实现数据的快速搜索或排序。其他时候，我们使用数据结构以便我们能做更少的事情：例如，栈的概念是更一般的数据结构的有限形式。这些限制为我们提供了保证，使我们能够更容易地推断程序。数据结构还提供有关算法复杂度的保证——为一项工作选择适当的数据结构对于编写良好的软件至关重要。

由于数据结构是更高层次的抽象，它们向我们展示了对数据组的操作，例如将项目添加到列表中，或在队列中查找最高优先级的项目。当数据结构提供操作时，我们可以将数据结构称为抽象数据类型（有时缩写为 ADT）。抽象数据类型可以最小化代码中的依赖关系，这在需要更改代码时很重要。由于您从较低级别的细节中抽象出来，因此一个数据结构与另一个数据结构共享的一些更高级别的共同点可以用来用另一个数据结构替换一个数据结构。

我们的编程语言配备了一组内置类型，例如整数和浮点数，这些类型允许我们使用机器处理器具有原生支持的数据对象。这些内置类型是处理器实际提供的抽象，因为内置类型隐藏了有关其执行和限制的详细信息。

例如，当我们使用浮点数时，我们主要关心它的值以及可以对其应用的操作。考虑计算斜边的长度

  let c := sqrt(a * a + b * b)

从上面生成的机器代码将使用常见的模式来计算这些值并累积结果。事实上，这些模式是如此重复，以至于创建了高级语言来避免这种冗余，并允许程序员思考计算的什么值而不是如何计算它。

这里有两个有用的相关概念

封装是指将常见模式分组到一个名称下，然后对其进行参数化，以实现对该模式的更高层次的理解。例如，乘法运算需要两个源值并将这两个值的积写入给定的目标。该操作由源和单个目标参数化。
抽象是一种将抽象的实现细节隐藏在抽象用户之外的机制。例如，当我们相乘数字时，我们不需要知道处理器实际使用的技术，我们只需要知道它的属性。

编程语言既是机器的抽象，也是封装机器内部细节的工具。例如，当编程语言充分封装用户以使其远离任何一台机器时，用编程语言编写的程序可以编译到几种不同的机器架构中。

在这本书中，我们对编程语言提供的抽象和封装进行了更进一步的步骤：当应用程序变得更加复杂时，编程语言的抽象变得过于低级而无法有效地管理。因此，我们在这些较低级别结构之上构建我们自己的抽象。我们甚至可以在这些抽象之上构建进一步的抽象。每次向上构建时，我们都会失去对较低级别实现细节的访问权限。虽然失去这种访问权限听起来像是一笔糟糕的交易，但它实际上是一笔非常划算的交易：我们主要关心的是解决手头的难题，而不是任何琐碎的决定，这些决定本来可以随意地用另一个决定代替。当我们能够在更高层次上思考时，我们就能免除这些负担。

我们在这本书中介绍的每个数据结构都可以被认为是一个单独的单元，它具有一组值和一组可以用来访问或更改这些值的操作。数据结构本身可以理解为数据结构的操作集以及每个操作的属性（即操作的作用以及我们预计需要多长时间）。

大O符号是一种常见的表达计算机代码性能的方式。该符号在内存中项目的数量和函数的平均性能之间建立了关系。对于一组 $n$ 个项目， $O(n)$ 表示特定函数平均将在该组 $n$ 个项目上执行 $n$ 次操作。 $O(1)$ 表示该函数始终执行恒定数量的操作，无论项目的数量如何。该符号仅表示算法复杂度，因此函数可能执行更多操作，但根据惯例， $n$ 的恒定倍数将被删除。

节点

我们首先查看的是节点结构。节点只是一个值容器，加上指向“下一个”节点的指针（该指针可能是null）。

以上是对结构的抽象

在某些语言中，结构被称为记录或类。某些其他语言不直接支持结构，而是允许使用其他结构（例如元组或列表）来构建它们。

这里，我们只关心节点包含某种形式的值，因此我们简单地说它的类型是“元素”，因为类型并不重要。在某些编程语言中，永远不需要指定类型（如动态类型语言，如 Scheme、Smalltalk 或 Python）。在其他语言中，类型可能需要限制为整数或字符串（如静态类型语言，如 C）。在其他语言中，包含元素类型的决定可以延迟到实际使用类型时（如支持泛型类型的语言，如 C++ 和 Java）。在任何这些情况下，将伪代码翻译成您自己的语言都应该比较简单。

每个指定的节点操作都可以很容易地实现

// Create a new node, with v as its contained value and next as
// the value of the next pointer
function make-node(v, node next): node
  let result := new node {v, next}
  return result
end

// Returns the value contained in node n
function get-value(node n): element
  return n.value
end

// Returns the value of node n's next pointer
function get-next(node n): node
  return n.next
end

// Sets the contained value of n to be v
function set-value(node n, v)
  n.value := v
end

// Sets the value of node n's next pointer to be new-next
function set-next(node n, new-next)
  n.next := new-next
  return new-next
end

原则上，我们更关心操作和实现策略，而不是结构本身和低级别实现。例如，我们更关心指定的时间要求，该要求指出所有操作花费的时间是 $O(1)$ 。上面的实现满足了这个标准，因为每个操作所需的时间是恒定的。另一种看待恒定时间操作的方式是将它们视为其分析不依赖于任何变量的操作。（符号 $O(1)$ 在下一章中进行了数学定义。现在，我们可以假设它只意味着恒定时间。）

由于节点只是一个值容器和指向另一个节点的指针的容器，因此节点数据结构本身（及其实现）是多么微不足道就不足为奇了。

从节点构建链

尽管节点结构很简单，但它实际上允许我们计算仅使用固定大小整数无法计算的东西。

但首先，我们将看一下不需要使用节点的程序。以下程序将从输入流（可以来自用户或文件）中读取一系列数字，直到遇到文件末尾，然后输出最大数字以及所有数字的平均值。

program(input-stream in, output-stream out)
  let total := 0
  let count := 0
  let largest :=  $-\infty$ 
  
  while has-next-integer(in):
    let i := read-integer(in)
    total := total + i
    count := count + 1
    largest := max(largest, i)
  repeat
   
  println out "Maximum: " largest
  
  if count != 0:
    println out "Average: " (total / count)
  fi
end

但现在考虑解决一个类似的任务：读取一系列数字，直到遇到文件末尾，然后输出最大数字以及所有能被最大数字整除的数字的平均值。这个问题不同，因为最大数字可能是最后输入的数字：如果要计算所有能被该数字整除的数字的平均值，则需要以某种方式记住它们。可以使用变量来记住之前的数字，但变量只能在输入的数字不多时帮助我们解决问题。

例如，假设我们给自己分配 200 个变量来保存用户输入的状态。再假设每个变量都有 64 位。即使我们对程序非常巧妙，它也只能计算 $2^{64\cdot 200}$ 种不同类型的输入的结果。虽然这是一个非常大的组合数，但一个包含 300 个 64 位数字的列表需要更多的组合才能被正确编码。（通常，这个问题被认为需要线性空间。所有只需要有限个变量的程序可以在常数空间内解决。）

与其内置限制（例如，只有常数个变量）来使编码复杂化，我们可以利用节点抽象的特性来允许我们记住计算机可以容纳的任意多个数字。

program(input-stream in, output-stream out)
  let largest :=  $-\infty$ 
  let nodes := null
  
  while has-next-integer(in):
    let i := read-integer(in)
    nodes := make-node(i, nodes) // contain the value i,
                                 // and remember the previous numbers too
    largest := max(largest, i)
  repeat
  println out "Maximum: " largest

  // now compute the averages of all factors of largest
  let total := 0
  let count := 0
  while nodes != null:
    let j := get-value(nodes)
    if j divides largest:
      total := total + j
      count := count + 1
    fi
    nodes := get-next(nodes)
  repeat
  if count != 0:
    println out "Average: " (total / count)
  fi
end

在上面，如果成功读取了n个整数，将调用make-noden次。这将需要创建n个节点（这些节点需要足够的空间来容纳每个节点的value和next字段，加上内部内存管理开销），因此内存需求将按 $O(n)$ 的顺序增长。类似地，我们构建这个节点链，然后再次遍历链，这将需要 $O(n)$ 步来创建链，然后还需要 $O(n)$ 步来遍历它。

注意，当我们遍历链中的数字时，实际上是按相反的顺序查看它们。例如，假设输入到我们程序中的数字是 4、7、6、30 和 15。在遇到 EOF 后，nodes 链将如下所示：

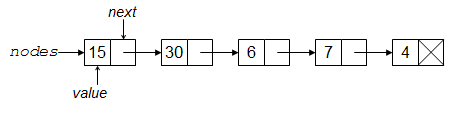
这种链通常被称为链表。但是，我们通常更喜欢考虑列表或序列，它们不是那么低级：链接的概念只是一个实现细节。虽然可以使用链来创建列表，但在本书中，我们将介绍其他几种创建列表的方法。目前，我们更关心节点的抽象能力，而不是它使用的一种方式。

上面的算法只使用了 make-node、get-value 和 get-next 函数。如果我们使用 set-next，我们可以改变算法以生成链，使其保持原始顺序（而不是反转它）。

要执行
用于执行此操作的伪代码；另外，TODO；可能应该考虑使用 set-value 的引人注目但不过于高级的应用。

program (input-stream in, output-stream out)
  let largest :=  $-\infty$ 
  let nodes := null
  let tail_node := null
  
  while has-next-integer (in):
    let i := read-integer (in)
    if (nodes == null)
      nodes := make-node(i, null) // construct first node in the list
      tail_node := nodes //there is one node in the list=> first and last are the same
    else
      tail_node := set-next (tail_node, make-node (i, null)) // append new node to the end of the list
    largest := max(largest, i)
  repeat
  println out "Maximum: " largest

  // now compute the averages of all factors of largest
  let total := 0
  let count := 0
  while nodes != null:
    let j := get-value(nodes)
    if j divides largest:
      total := total + j
      count := count + 1
    fi
    nodes := get-next(nodes)
  repeat
  if count != 0:
    println out "Average: " (total / count)
  fi
end

归纳原理

我们可以从节点构建的链是数学归纳原理的证明。

数学归纳法

假设你有一些关于数字 $P(n)$ 的性质。
如果你能证明当 $P(n)$ 成立时， $P(n+1)$ 也必须成立，那么
你只需要证明 $P(1)$ 成立，就可以证明对于所有自然数 $n$ ， $P(n)$ 成立。

例如，令性质 $P(n)$ 为语句“你可以创建一个容纳 $n$ 个数字的链”。这是一个关于自然数的性质，因为这句话对于 $n$ 的特定值是有意义的。

你可以创建一个容纳 5 个数字的链
你可以创建一个容纳 100 个数字的链
你可以创建一个容纳 1,000,000 个数字的链

与其证明我们可以创建长度为 5、100 和一百万的链，我们更愿意证明一般性语句 $P(n)$ 。上面第 2 步被称为 **归纳假设**；让我们证明我们可以证明它。

假设 $P(n)$ 成立。也就是说，我们可以创建一个包含 $n$ 个元素的链。现在我们必须证明 $P(n+1)$ 成立。
假设 chain 是 $n$ 元素链的第一个节点。假设 i 是我们想要添加到链中以创建 $n+1$ 长度链的某个数字。
以下代码可以为我们完成此操作

let bigger-chain := make-node(i, chain)

在这里，我们有了新的数字 i，它现在是 bigger-chain 的第一个链接所包含的值。如果 chain 包含 $n$ 个元素，那么 bigger-chain 必须包含 $n+1$ 个元素。

上面第 3 步被称为 **基本情况**，让我们证明我们可以证明它。

我们必须证明 $P(1)$ 成立。也就是说，我们可以创建一个包含一个元素的链。
以下代码可以为我们完成此操作

let chain := make-node(i, null)

因此，归纳原理表明，我们已经证明对于 $n$ 的所有值，我们可以创建包含 $n$ 个元素的链 $n\geq 1$ 。这是为什么呢？也许理解归纳的最佳方式是，它实际上是创建公式来描述无限多个证明的方法。在我们证明了语句对于 $P(1)$ （基本情况）成立后，我们可以将归纳假设应用于该事实来证明 $P(2)$ 成立。由于我们现在知道 $P(2)$ 成立，我们可以再次应用归纳假设来证明 $P(3)$ 必须成立。该原理表明，没有任何东西能阻止我们反复这样做，因此我们应该假设它在所有情况下都成立。

归纳法听起来可能是一种奇怪的证明方法，但它是一种非常有用的技术。使这种技术如此有用的原因是，它可以将一个听起来很困难的陈述，比如“证明 $P(n)$ 对所有 $n\geq 1$ 成立”分解成两个更小、更容易证明的陈述。通常情况下，基本情况很容易证明，因为它们根本不是一般性陈述。大部分证明工作通常都在归纳假设中，这通常需要巧妙地重新表述陈述，以“附加”一个 $n+1$ 情况的证明。

你可以将节点的包含值视为基本情况，而将节点的下一个指针视为归纳假设。就像数学归纳法一样，我们可以将存储任意数量元素的难题分解成更简单的存储一个元素的难题，然后有一个机制来附加更多元素。

对求和的归纳法

我们接下来要考虑的归纳法的例子在本质上更多地是代数性的。

假设我们给出了公式 ${\frac {(n)(n+1)}{2}}$ ，我们想要证明这个公式给出了前 $n$ 个数字的总和。作为第一个尝试，我们可能会尝试仅仅证明它对 1 成立。

{\frac {(1)(1+1)}{2}}=1=1

,

对 2 成立

{\frac {(2)(2+1)}{2}}=3=1+2

,

对 3 成立

{\frac {(3)(3+1)}{2}}=6=1+2+3

等等，但是我们会很快意识到，我们所谓的证明需要无限长的时间才能写出来！即使你完成了这个证明并证明它对前十亿个数字成立，但这并不一定意味着它对十亿零一或甚至一百亿成立。这是一个强烈的暗示，也许归纳法在这里会很有用。

假设我们想要证明给定的公式确实给出了前 n 个数字的总和，使用归纳法。第一步是证明基本情况；也就是说，我们必须证明它在 n = 1 时成立。这相对容易；我们只需要用 1 代替变量 n，我们得到 ( ${\frac {(1)(1+1)}{2}}=1$ )，这表明当 n = 1 时，公式是正确的。

现在进行归纳步骤。我们必须证明，如果公式对 j 成立，它对 j + 1 也成立。换句话说，假设我们已经证明了从 1 到 (j) 的总和是 ${\frac {((j))((j)+1)}{2}}$ ，我们想要证明从 1 到 (j+1) 的总和是 ${\frac {((j+1))((j+1)+1)}{2}}$ 。注意，这两个公式只是通过分别用 (j) 和 (j+1) 替换 n 得来的。

为了证明这个归纳步骤，首先要注意，要计算从 1 到 j+1 的总和，你只需计算从 1 到 j 的总和，然后加上 j+1。我们已经有了从 1 到 j 的总和的公式，当我们把 j+1 加到那个公式中时，我们得到了这个新公式： ${\frac {((j))((j)+1)}{2}}+(j+1)$ . 所以为了真正完成证明，我们只需要证明 ${\frac {((j))((j)+1)}{2}}+(j+1)={\frac {((j+1))((j+1)+1)}{2}}$ .