数据结构/哈希表
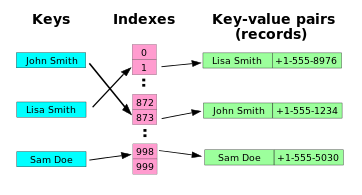
哈希表或哈希映射是一种数据结构,它将键与值关联起来。它最有效地支持的主要操作是查找:给定一个键(例如,一个人的姓名),找到相应的键值(例如,该人的电话号码)。它的工作原理是使用哈希函数将键转换为哈希值,哈希值是一个数字,哈希表使用它来定位所需的值。此哈希值直接映射到键/值对数组中的一个桶,因此得名哈希映射。映射方法让我们直接访问任何键/值对的存储位置。
哈希表<元素> 操作
make-hash-table(整数 n): 哈希表
- 创建一个具有 n 个桶的哈希表。
get-value(哈希表 h, 可比较的 key): 元素
- 返回给定 key 的元素的值。key 必须是某个可比较的类型。
set-value(哈希表 h, 可比较的 key, 元素 new-value)
- 将给定 key 的数组元素设置为等于 new-value。key 必须是某个可比较的类型。
remove(哈希表 h, 可比较的 key)
- 从哈希表中删除给定 key 的元素。key 必须是某个可比较的类型。
哈希表通常用于实现关联数组、集合和缓存。与数组类似,哈希表在平均情况下提供恒定时间的O(1) 查找,无论表中有多少项。在大多数哈希表方案中,(希望很少见的)最坏情况查找时间是 O(n)。[1] 与其他关联数组数据结构相比,当我们需要存储大量数据记录时,哈希表最有用。
哈希表可以用作内存中的数据结构。哈希表也可以用于持久数据结构;数据库索引通常使用基于哈希表的磁盘数据结构。
哈希表还用于在许多数据压缩实现中加快字符串搜索。
一个好的哈希函数对于哈希表的良好性能至关重要。选择一个糟糕的哈希函数可能会导致聚类行为,在这种行为中,键映射到同一个哈希桶(即冲突)的概率明显高于随机函数的预期。在任何哈希实现中,冲突发生的非零概率是不可避免的,但解决冲突的操作次数通常与映射到同一个桶的键的数量成线性关系,因此过多的冲突会显著降低性能。此外,一些哈希函数在计算上很昂贵,因此计算哈希值所花费的时间(以及在某些情况下内存)可能会很繁重。
选择一个好的哈希函数很棘手。文献中充斥着糟糕的选择,至少从现代标准来看是这样的。例如,在《计算机程序设计艺术》中,Knuth 提倡的非常流行的乘法哈希算法具有特别糟糕的聚类行为(见下面的参考文献)。然而,由于糟糕的哈希算法仅仅会降低特定输入键分布下哈希表的性能,因此这种问题经常得不到检测。
文献中关于选择哈希函数的标准也很稀少。与大多数其他基本算法和数据结构不同,对于什么是“好的”哈希函数,还没有普遍共识。本节的其余部分将按照三个标准进行组织:简单性、速度和强度,并介绍已知根据这些标准表现良好的算法。
简单性和速度很容易客观地测量(例如,通过代码行数和 CPU 基准测试),但强度是一个更难以捉摸的概念。显然,加密哈希函数(如 SHA-1)将满足哈希表所需的相对宽松的强度要求,但它们的缓慢和复杂性使其不具有吸引力。事实上,即使是加密哈希也不能提供对想要通过选择所有都散列到同一个桶的键来降低哈希表性能的对手的保护。对于这些特殊情况,应该使用通用哈希函数,而不是任何一个静态哈希函数,无论它多么复杂。
由于没有衡量哈希函数强度的标准方法,目前的技术是采用一系列统计测试来衡量哈希函数是否可以很容易地与随机函数区分开。可以说,最重要的测试是确定哈希函数是否显示雪崩效应,它本质上是指输入键的任何一位变化平均应该影响输出中的二分之一的位。Bret Mulvey 提倡特别测试严格雪崩条件,它表明,对于任何一位变化,每个输出位应该以二分之一的概率改变,独立于键中的其他位。纯粹的加法哈希函数,例如CRC,惨败地未能满足这个更强的条件。
显然,一个强大的哈希函数应该具有均匀分布的哈希值。Bret Mulvey 建议使用基于2 的幂哈希表大小的卡方检验,大小范围从 21 到 216。与许多其他用于衡量哈希函数的建议方法相比,此测试的敏感度要高得多,它在许多流行的哈希函数中发现了问题。
幸运的是,有一些好的哈希函数满足所有这些标准。最简单的类在内循环的每次迭代中都消耗输入键的一个字节。在这个类中,简单性和速度密切相关,因为快速算法根本没有时间执行复杂的计算。在这些算法中,一个表现特别好的算法是 Jenkins One-at-a-time 哈希算法,它改编自Bob Jenkins(它的创造者)的文章。
uint32 joaat_hash(uchar *key, size_t len)
{
uint32 hash = 0;
size_t i;
for (i = 0; i < len; i++)
{
hash += key[i];
hash += (hash << 10);
hash ^= (hash >> 6);
}
hash += (hash << 3);
hash ^= (hash >> 11);
hash += (hash << 15);
return hash;
}

右侧显示了此哈希的雪崩行为。该图像是使用 Bret Mulvey 的 Hash.cs 工具集 中的 AvalancheTest 制作的。每行对应输入中的一个位,每列对应输出中的一个位。绿色方块表示良好的混合行为,黄色方块表示弱混合行为,红色表示没有混合。最后一个字节中只有几个位混合不好,这比许多广泛使用的哈希函数的性能要好得多。
许多常用的哈希函数在进行这种严格的雪崩测试时表现不佳。例如,广受好评的 FNV 哈希在短键的情况下,显示了许多位根本没有混合。请参阅 Bret Mulvey 对 FNV 的评估,以获取更全面的分析。
如果速度比简单性更重要,那么那些每次迭代消耗多个字节块的哈希函数类可能值得关注。其中最复杂的是 Bob Jenkins 的“lookup3”,它以 12 字节(96 位)块消耗输入。不过请注意,使用此哈希带来的任何速度改进,只有在大型键的情况下才可能有用,并且更高的复杂性也可能带来速度方面的后果,例如阻止优化编译器内联哈希函数。Bret Mulvey 分析了 早期版本 lookup2,发现它具有极佳的雪崩行为。
哈希函数的一个理想特性是,可以简单地通过掩码来将哈希值(通常为 32 位)转换为特定大小哈希表的桶索引,仅保留较低的 k 位以用于大小为 2k 的表(此操作等效于计算哈希值 模 表的大小)。此特性允许使用增量加倍哈希表大小的技术——旧表中的每个桶在新的表中仅映射到两个桶。由于 FNV 哈希使用 XOR 折叠,因此它不具有此特性。一些旧的哈希函数更糟糕,要求表的大小是素数而不是 2 的幂,再次将桶索引计算为哈希值模表的大小。通常,这种要求是函数本质上较弱的标志;使用素数表大小是使用更强函数的糟糕替代品。
冲突解决
[edit | edit source]如果两个键映射到同一个索引,则相应的记录不能存储在同一个位置。因此,如果该位置已被占用,我们必须找到另一个位置来存储新记录,并且必须以一种可以在以后查找时找到它的方式来执行此操作。
为了说明良好的冲突解决策略的重要性,请考虑以下结果,该结果使用 生日悖论 推导出。即使我们假设我们的哈希函数在数组上输出 均匀分布 的随机索引,即使对于具有 100 万个条目的数组,在它包含 2500 条记录之前至少发生一次冲突的概率为 95%。
有很多冲突解决技术,但最受欢迎的是链式哈希法和开放定址法。
链式哈希法
[edit | edit source]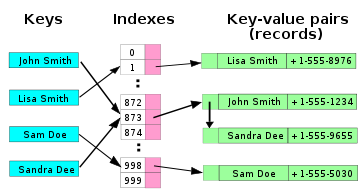
在最简单的链式哈希表技术中,数组中的每个槽位都引用一个 链表,其中包含插入到相同槽位的记录。插入需要找到正确的槽位,并在该槽位的列表的任一端追加;删除需要搜索列表并删除。
链式哈希表比开放定址哈希表具有优势,因为删除操作很简单,并且可以更长时间地推迟表的大小调整,因为即使每个槽位都被使用,性能的 下降也更加平缓。实际上,许多链式哈希表可能根本不需要调整大小,因为随着表填满,性能下降是线性的。例如,一个包含其推荐容量两倍数据的链式哈希表,其平均速度大约仅为相同表在其推荐容量下的两倍慢。
链式哈希表继承了链表的缺点。在存储小记录时,链表的开销可能很大。另一个缺点是遍历链表的 缓存性能 很差。
可以使用其他数据结构来代替链表。例如,使用 自平衡树,可以将哈希表的理论最坏情况时间从 O(n) 降至 O(log n)。但是,由于每个列表都希望很短,因此这种方法通常效率低下,除非哈希表设计为以满负荷运行,或者发生异常高的冲突率,就像在旨在导致冲突的输入中可能会发生的那样。 动态数组 也可以用来减少空间开销,并在记录较小时提高缓存性能。
一些链式实现使用了一种优化,即每个链的第一个记录存储在表中。虽然这可以提高性能,但通常不推荐这样做:具有合理负载因子的链式表包含大量的空槽位,而较大的槽位大小会导致它们浪费大量空间。
开放定址法
[edit | edit source]
开放定址哈希表可以将记录直接存储在数组中。通过探测来解决哈希冲突,或者在数组中搜索备用位置(探测序列),直到找到目标记录,或者找到一个未使用的数组槽位,这表明表中没有这样的键。众所周知的探测序列包括
- 线性探测
- 其中探测之间的间隔是固定的——通常为 1,
- 二次探测
- 其中探测之间的间隔线性增加(因此,索引由二次函数描述),以及
- 双重哈希
- 其中探测之间的间隔对于每个记录是固定的,但通过另一个哈希函数计算得出。
这些方法之间主要权衡在于,线性探测具有最佳的缓存性能,但对聚类最为敏感,而双重哈希的缓存性能很差,但几乎没有聚类现象;二次探测在这两个方面都处于中间位置。双重哈希可能比其他形式的探测需要更多的计算。一些开放定址方法,如 后进先出哈希 和 布谷鸟哈希 会在数组中移动现有的键以腾出空间存放新键。这提供了比基于探测的方法更好的最大搜索时间。
对开放定址哈希表性能的关键影响是负载因子;即数组中使用的槽位的比例。随着负载因子增加到 100%,找到或插入给定键可能需要的探测次数急剧增加。一旦表已满,探测算法甚至可能无法终止。即使使用良好的哈希函数,负载因子通常也限制在 80%。不良的哈希函数即使在非常低的负载因子下也会表现出较差的性能,因为它们会产生大量的聚类。导致哈希函数聚类的因素尚不清楚,并且很容易无意中编写会导致严重聚类的哈希函数。
示例伪代码
[edit | edit source]以下 伪代码 是开放定址哈希表的实现,它使用线性探测和单槽位步进,这是一种常见的方法,如果哈希函数很好,它将非常有效。lookup、set 和 remove 函数中的每一个都使用一个共同的内部函数 findSlot 来定位数组槽位,该槽位要么包含给定键,要么应该包含给定键。
record pair { key, value }
var pair array slot[0..numSlots-1]
function findSlot(key)
i := hash(key) modulus numSlots
loop
if slot[i] is not occupied or slot[i].key = key
return i
i := (i + 1) modulus numSlots
function lookup(key)
i := findSlot(key)
if slot[i] is occupied // key is in table
return slot[i].value
else // key is not in table
return not found
function set(key, value)
i := findSlot(key)
if slot[i].key = key
// (Key already in table. Update value.)
slot[i].value := value
else
// (Insert key and value in un-occupied slot.)
// (But first, make sure insert won't overload the table)
if the table is almost full
rebuild the table larger (note 1)
i := findSlot(key)
slot[i].key := key
slot[i].value := value
另一个展示开放定址技术的示例。所呈现的函数是转换 Internet 协议地址的每个部分(4),其中 NOT 是按位 NOT,XOR 是按位 XOR,OR 是按位 OR,AND 是按位 AND,<< 和 >> 是左移和右移
// key_1,key_2,key_3,key_4 are following 3-digit numbers - parts of ip address xxx.xxx.xxx.xxx
function ip(key parts)
j := 1
do
key := (key_2 << 2)
key := (key + (key_3 << 7))
key := key + (j OR key_4 >> 2) * (key_4) * (j + key_1) XOR j
key := key AND _prime_ // _prime_ is a prime number
j := (j+1)
while collision
return key
- 注意 1
- 重建表需要分配一个更大的数组,并递归地使用 set 操作将旧数组的所有元素插入到新的更大的数组中。通常会 指数地 增加数组大小,例如将旧数组大小加倍。
function remove(key)
i := findSlot(key)
if slot[i] is unoccupied
return // key is not in the table
j := i
loop
j := (j+1) modulus numSlots
if slot[j] is unoccupied
exit loop
k := hash(slot[j].key) modulus numSlots
if (j > i and (k <= i or k > j)) or
(j < i and (k <= i and k > j)) (note 2)
slot[i] := slot[j]
i := j
mark slot[i] as unoccupied
- 注意 2
- 对于集群中的所有记录,它们的自然哈希位置与其当前位置之间不能有空槽(否则查找将在找到记录之前终止)。在伪代码的这一步,i 是一个空槽,它可能会使集群中后续记录的此属性无效。j 是这样后续记录。k 是原始哈希,如果不存在冲突,则位于j 的记录将在哈希表中自然落地。此测试询问位于j 的记录是否相对于集群的必需属性(现在i 是空的)处于无效位置。
另一种删除技术是简单地将该槽标记为已删除。但是,这最终需要重建表以简单地删除已删除的记录。上述方法提供 O(1) 更新和删除现有记录,如果表的最高水位标记增长,则偶尔会重建。
上述 O(1) 删除方法仅在使用单槽步长的线性探测哈希表中才有可能。在需要在一个操作中删除许多记录的情况下,标记要删除的槽位并稍后重建可能更高效。
与开放寻址相比,链式哈希表具有以下优点
- 它们易于有效地实现,并且只需要基本的数据结构。
- 从编写合适的哈希函数的角度来看,链式哈希表对集群不敏感,只需要最小化冲突。开放寻址依赖于更好的哈希函数来避免集群。如果新手程序员可以添加自己的哈希函数,这一点尤其重要,但即使是经验丰富的程序员也可能被意外的集群效应所困扰。
- 它们的性能下降更加平缓。尽管随着表的填充,链条越来越长,但链式哈希表不会“填满”,并且不会像开放寻址的接近满载表那样出现查找时间突然增加。(参见右侧)
- 如果哈希表存储大型记录,每条记录大约 5 个或更多个字,则链式寻址比开放寻址使用更少的内存。
- 如果哈希表是稀疏的(即,它有一个包含许多空数组槽的大数组),由于其外部存储,即使对于每条记录只有 2 到 4 个字的小记录,链式寻址也比开放寻址使用更少的内存。

对于小型记录大小(几个字或更少),与链式寻址相比,就地开放寻址的优点是
- 它们比链式寻址更节省空间,因为它们不需要存储任何指针或在哈希表之外分配任何额外的空间。简单的链表每个元素需要一个字的开销。
- 插入避免了内存分配的时间开销,甚至可以在没有内存分配器的情况下实现。
- 由于它使用内部存储,开放寻址避免了链式寻址的外部存储所需的额外间接寻址。它还具有更好的 局部性,特别是对于线性探测。对于小型记录大小,这些因素可以产生比链式寻址更好的性能,特别是对于查找。
- 它们更容易 序列化,因为它们不使用指针。
另一方面,对于大型元素来说,普通的开放寻址是一个糟糕的选择,因为这些元素会填满整个缓存行(抵消了缓存优势),并且在大型空表槽位上浪费了大量空间。如果开放寻址表只存储对元素的引用(外部存储),它即使对于大型记录也使用与链式寻址相当的空间,但会失去其速度优势。
总的来说,开放寻址更适合用于具有小型记录的哈希表,这些记录可以存储在表中(内部存储)并适合缓存行。它们特别适合于一个字或更少的元素。在预期表具有高负载因子、记录很大或数据大小可变的情况下,链式哈希表通常执行得一样好或更好。
最终,明智地使用任何类型的哈希表算法通常都足够快;并且在哈希表代码中花费的计算百分比很低。内存使用量很少被认为是过度的。因此,在大多数情况下,这些算法之间的差异是微不足道的,其他考虑因素通常会起作用。
合并哈希是链式寻址和开放寻址的混合体,它在表本身内链接节点链。与开放寻址一样,它比链式寻址实现了更高的空间利用率和(略微降低的)缓存优势。与链式寻址一样,它不会出现集群效应;实际上,表可以高效地填充到很高的密度。与链式寻址不同,它不能具有超过表槽的元素。
如果所有将要使用的键都事先已知,并且没有更多适合哈希表的键,则可以使用 完美哈希 来创建完美哈希表,其中不会发生冲突。如果使用 最小完美哈希,哈希表中的每个位置也可以使用。
完美哈希提供了一个哈希表,其中在最坏情况下进行查找的时间是恒定的。这与链式寻址和开放寻址方法形成对比,在这些方法中,查找时间平均较低,但可能任意大。存在用于在插入键时维护完美哈希函数的方法,称为 动态完美哈希。另一种更简单的替代方案,它也提供了最坏情况下的恒定查找时间,是 布谷鸟哈希。
对于冲突,最简单的解决方案可能是用新值替换已经存在于槽中的值,或者不太常见的是,删除要插入的记录。在以后的搜索中,这可能会导致搜索无法找到已插入的记录。此技术对于实现缓存特别有用。
与之类似的更节省空间的解决方案是使用 位数组(一个一位字段数组)作为我们的表。最初所有位都设置为零,当我们插入一个键时,我们将相应的位设置为一。不会出现假阴性,但可能会出现 假阳性,因为如果搜索找到 1 位,它将声称该值已找到,即使它只是另一个碰巧哈希到同一个数组槽中的值。实际上,这样的哈希表只是一个特定的 布隆过滤器 类型。
使用良好的哈希函数,哈希表通常可以包含大约 70%–80% 的表槽数,并且仍然可以正常执行。根据冲突解决机制的不同,性能可能会随着添加更多元素而逐渐或急剧下降。为了解决这个问题,当负载因子超过某个阈值时,我们会分配一个新的、更大的表,并将原始表中的所有内容添加到这个新表中。例如,在 Java 的 HashMap 类中,默认负载因子阈值为 0.75。
这可能是一个非常昂贵的操作,而且它的必要性是哈希表的一个缺点。实际上,一些天真的执行此操作的方法,例如每次添加新元素时将表扩大一个,会大幅降低性能,从而使哈希表变得无用。但是,如果我们将表扩大某个固定百分比,例如 10% 或 100%,则可以使用 摊销分析 来证明这些调整大小非常不频繁,以至于每次查找的平均时间仍然是恒定时间。为了了解这是为什么,假设一个使用链式寻址的哈希表从最小大小 1 开始,并且每次填满超过 100% 时都加倍。如果最终它包含 n 个元素,那么对所有调整大小执行的总添加操作为
- 1 + 2 + 4 + ... + n = 2n - 1。
因为调整大小的成本构成一个 几何级数,总成本为 O(n)。但我们还执行 n 次操作来添加最初的 n 个元素,因此添加 n 个元素(包含调整大小)的总时间为 O(n),即每个元素的摊销时间为 O(1)。
另一方面,一些哈希表实现,特别是在 实时系统 中,无法承受一次性扩大哈希表的价格,因为它可能会中断时间敏感的操作。一个简单的办法是最初为预期元素数量分配足够的存储空间,并禁止添加太多元素。另一种有用但更占内存的技术是逐步执行调整大小
- 分配新的哈希表,但保留旧的哈希表,并在查找时检查这两个表。
- 每次执行插入时,将该元素添加到新表中,并将 k 个元素从旧表移动到新表中。
- 当从旧表中删除所有元素后,释放它。
为了确保在新的表本身需要扩大之前完全复制旧的表,在调整大小期间将表的尺寸增加至少 (k + 1)/k 倍是必要的。
线性哈希 是一种允许增量哈希表扩展的哈希表算法。它使用单个哈希表实现,但具有两种可能的查找函数。
降低表格调整大小成本的另一种方法是选择一种哈希函数,以便在调整表格大小时,大多数值的哈希值不会改变。这种方法称为一致性哈希,在基于磁盘和分布式哈希中很普遍,因为在这些情况下,调整大小的成本非常高。
哈希表将数据存储在伪随机位置,因此以排序方式访问数据是一个非常耗时的操作。其他数据结构,例如自平衡二叉搜索树,通常运行速度更慢(因为它们的查找时间为 O(log n)),而且比哈希表更复杂,但始终维护着排序的数据结构。参见哈希表和自平衡二叉搜索树的比较。
虽然哈希表查找平均使用常数时间,但花费的时间可能很长。评估一个好的哈希函数可能是一个缓慢的操作。特别是,如果可以使用简单的数组索引,这通常更快。
哈希表通常表现出较差的局部性,也就是说,要访问的数据在内存中看似随机分布。由于哈希表会导致访问模式四处跳跃,这会导致微处理器缓存未命中,从而导致长时间延迟。紧凑的数据结构(如数组),使用线性搜索进行搜索,如果表相对较小,并且密钥比较起来很便宜,例如使用简单的整数密钥,则可能更快。根据摩尔定律,缓存大小呈指数级增长,因此被认为“小”的可能也在增加。最佳性能点因系统而异;例如,在Parrot上的一个试验表明,它的哈希表在除最琐碎的情况(一到三个条目)之外的所有情况下都优于线性搜索。
更重要的是,哈希表更难编写和使用,而且容易出错。哈希表要求为每种密钥类型设计一个有效的哈希函数,在许多情况下,这比为自平衡二叉搜索树所需的对照函数更难,也更耗时。在开放寻址哈希表中,创建糟糕的哈希函数甚至更容易。
此外,在某些应用程序中,一个了解哈希函数的黑客可能能够向哈希提供信息,通过导致过度冲突来创建最坏情况的行为,从而导致非常糟糕的性能(即,拒绝服务攻击)。在关键应用程序中,可以使用通用哈希,或者可能更适合使用具有更好最坏情况保证的数据结构。有关详细信息,请参阅 Crosby 和 Wallach 的通过算法复杂性攻击实现拒绝服务。
可扩展哈希和线性哈希是哈希算法,它们用于数据库算法的上下文中,例如索引文件结构,甚至数据库的主要文件组织。通常,为了使搜索对大型数据库可扩展,搜索时间应与 log N 或接近常数成正比,其中 N 是要搜索的记录数。可以使用树结构实现 log N 搜索,因为扇出度和树的短小与查找记录所需的步骤数相关,因此树的高度是查找记录位置所需的磁盘访问次数的最大值。但是,也使用哈希表,因为磁盘访问的成本可以用磁盘访问单位来计算,并且该单位通常是一个数据块。由于哈希表在最佳情况下可以用一次或两次访问找到密钥,因此哈希表索引在检索联接操作期间的一组记录时通常被认为更快,例如。
SELECT * from customer, orders where customer.cust_id = orders.cust_id and cust_id = X
例如,如果订单对 cust_id 有一个哈希索引,那么找到包含与 cust_id = X 匹配的订单记录位置的块需要常数时间。(虽然,如果订单的值类型是订单 ID 列表,那么这样更好,这样哈希密钥对于每个订单批次只有一个唯一的 cust_id,以避免不必要的冲突)。
可扩展哈希和线性哈希有一些相似之处:冲突被认为是不可避免的,并且是算法的一部分,其中添加了冲突空间的块或桶;需要传统的良好哈希函数范围,但哈希值通过动态地址函数转换;在可扩展哈希中,使用位掩码屏蔽掉不需要的位,但该掩码长度会周期性地增加一,使可用地址空间翻倍;同样在可扩展哈希中,有一个指向目录地址空间的间接地址,目录条目与另一个地址(指针)配对,该地址指向包含键值对的实际块;目录中的条目对应于位掩码哈希值(因此条目数等于最大位掩码值 + 1,例如,一个 2 位位掩码可以寻址一个包含 00 01 10 11 的目录,或者 3 + 1 = 4)。
在线性哈希中,传统的哈希值也使用位掩码进行掩码,但如果生成的较小哈希值低于“分割”变量,则原始哈希值使用一个位长度更大的位掩码进行掩码,使生成的哈希值寻址最近添加的块。分割变量在 0 和当前最大位掩码值之间递增,例如,一个 2 位的位掩码,或者在线性哈希的术语中,一个“级别”为 2,分割变量将在 0 到 3 之间。当分割变量达到 4 时,级别增加 1,因此在分割变量的下一轮中,它将在 0 到 7 之间,并在达到 8 时再次重置。
分割变量递增地允许增加地址空间,因为添加了新块;添加新块的决定发生在插入键值时,并且键值溢出到键值哈希到的特定块。此溢出位置可能与分割变量指向的要分割的块完全无关。然而,随着时间的推移,预计在给定一个将条目均匀分布在所有可寻址块中的良好随机哈希函数的情况下,实际需要分割的块(因为它们已经溢出)会以循环方式轮流获得它们的分割机会,因为分割值在 0-N 之间,其中 N 是 2 的 Level 次方的因子,Level 是每次分割变量达到 N 时增加的变量。
可扩展哈希和线性哈希都一次添加一个新块。
在可扩展哈希中,块溢出(一个新的键值与 B 个其他键值冲突,其中 B 是块的大小)通过检查“本地”的位掩码大小来处理,称为“本地深度”,这是一个必须与块一起存储的属性。目录结构也具有一个深度,即“全局深度”。如果本地深度小于全局深度,则本地深度加 1,并将所有键值重新哈希并通过现在更长一位的位掩码进行传递,将它们放置在当前块或另一个块中。如果另一个块恰好在目录中查找时是同一个块,则添加一个新块,并且指向另一个块的目录条目被设置为指向新块。为什么目录中会有条目,其中两个条目指向同一个块?这是因为如果本地深度等于目录的全局深度,这意味着目录的位掩码没有足够的位来处理块的位掩码长度的增加,因此目录必须增加其位掩码长度,但这意味着目录现在使可寻址条目的数量翻倍。由于一半的可寻址条目不存在,因此目录只需将指针复制到新条目中,例如,如果目录具有针对 00、01、10、11 的条目,或者一个 2 位掩码,并且它变成一个 3 位掩码,那么 000 001 010 011 100 101 110 111 成为新的条目,00 的块地址转到 000 和 001;01 的指针转到 010 和 011,10 转到 100 和 101 等等。因此,这会产生两种目录条目指向同一个块的情况。虽然将要溢出的块现在可以通过将第二个指针重定向到一个新添加的块来添加一个新块,但其他原始块将有两个指向它们的指针。当轮到它们分割时,该算法将检查本地深度与全局深度,这次发现本地深度更小,因此不需要目录分割,只需添加一个新块,并将第二个目录指针从指向先前块更改为指向新块。
在线性哈希中,添加一个具有相似哈希值的块不会在块溢出时立即发生,因此会创建一个溢出块并将其附加到溢出块。但是,块溢出表明需要更多空间,这可以通过分割由“split”变量指向的块来实现,该变量最初为零,因此最初指向块零。分割是通过获取分割块中所有的键值对以及它的溢出块(如果有),并再次哈希键,但使用长度为当前级别 + 1 的位掩码来实现的。这将导致两个块地址,一些将是旧的块编号,而另一些将是
a2 = old block number + ( N times 2 ^ (level) )
- 原理
令 m = N 乘以 2 的 level 次方;如果 h 是原始的哈希值,并且旧的块编号 = h 模 m,现在新的块编号是 h 模 (m * 2),因为 m * 2 = N 乘以 2 的 (level+1) 次方,那么新的块编号要么是 h 模 m(如果 (h / m) 是偶数,所以将 h/m 除以 2 会留下零余数,因此不会改变余数),要么是 (h 模 m) + m(因为 h / m 是奇数,将 h / m 除以 2 会留下 m 的余数,加上原始余数)。(相同的原理适用于可扩展哈希深度递增)。
如上所述,一个新的块将使用编号 a2 创建,该编号通常会出现在之前的 a2 值 + 1 处。完成此操作后,split 变量会递增,以便下一个 a2 值将再次是旧的 a2 + 1。这样,每个块最终都会被 split 变量覆盖,所以每个块都会被预先重新哈希到额外的空间,而新的块会增量添加。不再需要的溢出块会被丢弃,如果需要,则用于后面的垃圾回收,或者通过链接放到可用的空闲块列表中。
当 split 变量达到 (N 乘以 2 的 level 次方) 时,level 会递增,而 split 变量会被重置为零。在下一轮中,split 变量现在将从零遍历到 (N 乘以 2 的 (旧的 level + 1) 次方),这正是上一轮开始时的块数,但包含了上一轮创建的所有块。
可以看出,可扩展哈希需要空间来存储一个目录,该目录的大小可以翻倍。
由于两种算法的空间都以每次一个块的速度增加,如果块具有已知的最大尺寸或固定尺寸,那么将块映射为按顺序附加到文件的块是直截了当的。
在可扩展哈希中,将目录存储为一个单独的文件是合乎逻辑的,因为可以通过将目录文件附加到末尾来适应翻倍。除了将块附加到其末尾之外,单独的块文件不需要更改。
线性哈希的头部信息的大小不会增加:基本上只需要记录 N、level 和 split 的值,因此可以将它们作为头部合并到固定块大小的线性哈希存储文件中。
但是,线性哈希需要空间来存储溢出块,这最好存储在另一个文件中,否则在线性哈希文件中寻址块不会像将块编号乘以块大小然后加上 N、level 和 split 的空间那样直截了当。
在下一节中,将提供线性哈希在 Java 中的完整示例,使用线性哈希的内存中实现,以及将块作为文件管理到文件目录中的代码,整个文件目录的内容代表持久化的线性哈希结构。
虽然许多编程语言已经提供了哈希表的功能,[2]但仍有几个值得一提的独立实现。
- Google Sparse Hash Google SparseHash 项目包含几个在 Google 使用的哈希映射实现,具有不同的性能特征,包括一个针对空间优化的实现和一个针对速度优化的实现。内存优化的实现非常节省内存,每个条目只有 2 位的开销。
- MCT 提供与 Google 的
dense_hash_map相似的哈希表,但对包含的值没有限制;它还具有异常安全性并支持 C++0x 功能。 - 许多运行时语言和/或标准库使用哈希表来实现它们对关联数组的支持,因为哈希表的效率很高。
文件-块管理例程不存在,因此可以添加这些例程来使其成为数据库哈希索引的真实实现。
一个完整的页面根据 (局部深度) 位进行分割,首先通过收集所有指向完整页面的目录索引,根据 d 位是 0 还是 1 更新指针(对应于第一个和第二个新页面),然后在哈希每个键并使用每个哈希的 d 位来查看要分配到哪个页面之后,重新加载所有键值对。每个新页面的局部深度比旧页面的局部深度大 1,以便下次分割时可以使用下一个 d 位。
PAGE_SZ = 20
class Page:
def __init__(self):
self.m = {}
self.d = 0
def full(self):
return len(self.m) > PAGE_SZ
def put(self,k,v):
self.m[k] = v
def get(self,k):
return self.m.get(k)
class EH:
def __init__(self):
self.gd = 0
p = Page()
self.pp= [p]
def get_page(self,k):
h = hash(k)
p = self.pp[ h & (( 1 << self.gd) -1)]
return p
def put(self, k, v):
p = self.get_page(k)
if p.full() and p.d == self.gd:
self.pp = self.pp + self.pp
self.gd += 1
if p.full() and p.d < self.gd:
p.put(k,v);
p1 = Page()
p2 = Page()
for k2 in p.m.keys():
v2 = p.m[k2]
h = k2.__hash__()
h = h & ((1 << self.gd) -1)
if (h | (1 << p.d) == h):
p2.put(k2,v2)
else:
p1.put(k2,v2)
l = []
for i in xrange(0, len(self.pp)):
if self.pp[i] == p:
l.append(i)
for i in l:
if (i | ( 1 << p.d) == i):
self.pp[i] = p2
else:
self.pp[i] = p1
p1.d = p.d + 1
p2.d = p1.d
else:
p.put(k, v)
def get(self, k):
p = self.get_page(k)
return p.get(k)
if __name__ == "__main__":
eh = EH()
N = 10000
l = []
for i in range(0,N):
l.append(i)
import random
random.shuffle(l)
for i in l:
eh.put(i,i)
print l
for i in range(0, N):
print eh.get(i)
对上述 Python 代码的直接 Java 翻译,经过测试可以工作。
package ext_hashing;
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
import java.util.Random;
public class EH2<K, V> {
static class Page<K, V> {
static int PAGE_SZ = 20;
private Map<K, V> m = new HashMap<K, V>();
int d = 0;
boolean full() {
return m.size() > PAGE_SZ;
}
void put(K k, V v) {
m.put(k, v);
}
V get(K k) {
return m.get(k);
}
}
int gd = 0;
List<Page<K, V>> pp = new ArrayList<Page<K, V>>();
public EH2() {
pp.add(new Page<K, V>());
}
Page<K, V> getPage(K k) {
int h = k.hashCode();
Page<K, V> p = pp.get(h & ((1 << gd) - 1));
return p;
}
void put(K k, V v) {
Page<K, V> p = getPage(k);
if (p.full() && p.d == gd) {
List<Page<K, V>> pp2 = new ArrayList<EH2.Page<K, V>>(pp);
pp.addAll(pp2);
++gd;
}
if (p.full() && p.d < gd) {
p.put(k, v);
Page<K, V> p1, p2;
p1 = new Page<K, V>();
p2 = new Page<K, V>();
for (K k2 : p.m.keySet()) {
V v2 = p.m.get(k2);
int h = k2.hashCode() & ((1 << gd) - 1);
if ((h | (1 << p.d)) == h)
p2.put(k2, v2);
else
p1.put(k2, v2);
}
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < pp.size(); ++i)
if (pp.get(i) == p)
l.add(i);
for (int i : l)
if ((i | (1 << p.d)) == i)
pp.set(i, p2);
else
pp.set(i, p1);
p1.d = p.d + 1;
p2.d = p1.d;
} else
p.put(k, v);
}
public V get(K k) {
return getPage(k).get(k);
}
public static void main(String[] args) {
int N = 500000;
Random r = new Random();
List<Integer> l = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
l.add(i);
}
for (int i = 0; i < N; ++i) {
int j = r.nextInt(N);
int t = l.get(j);
l.set(j, l.get(i));
l.set(i, t);
}
EH2<Integer, Integer> eh = new EH2<Integer, Integer>();
for (int i = 0; i < N; ++i) {
eh.put(l.get(i), l.get(i));
}
for (int i = 0; i < N; ++i) {
System.out.printf("%d:%d , ", i, eh.get(i));
if (i % 10 == 0)
System.out.println();
}
}
}
(可用于任意大小的简单数据库索引,(几乎?))
这段代码源于对更大 Java HashMap 的需求。最初,一个 Java HashMap 标准对象用作 Map 来索引一个类似堆的数据库文件(DBF 格式)。但后来,遇到一个文件,其中包含如此多的记录,以至于抛出了 OutOfMemoryError,因此线性哈希似乎是一种作为基于磁盘的索引方案使用的简单算法。
最初,线性哈希是在 Java Map 接口后面实现的,主要是 put(k,v) 和 get(k,v) 方法。使用了泛型,以免过于关注键和值的细节。
自定义转储到 System.err 用于验证块是否正在创建、填充,以及溢出块的数量是否如预期(数量 = 1)。所有这些都是在纯内存中实现的。
后来,引入了标准的 Java 解耦,其中原始的 LHMap2 类接受事件监听器,例如当需要一个块时。然后,监听器被实现为一个块文件管理器,只要在块列表上遇到空块就将块加载到内存 LHMap2 对象的块列表中,并检查虚拟机运行时空闲内存是否不足,并通过将块保存到磁盘文件并然后主动调用系统垃圾收集器来使用基本的先到先出(FIFO)缓存删除算法(而不是最近最少使用(LRU),也不是最不常使用)来删除块。
由于存在一个应用程序用例,即外部索引一个大型 DBF 表,因此该用例被用作算法实现的主要测试工具。
package linearhashmap;
import java.io.Externalizable;
import java.io.IOException;
import java.io.ObjectInput;
import java.io.ObjectOutput;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Iterator;
import java.util.LinkedList;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.TreeMap;
import java.util.TreeSet;
/**
*
* @param <K>
* key type , must implement equals() and hashCode()
* @param <V>
* value type
*
*
*/
public class LHMap2<K, V> implements Map<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 3095071852466632996L;
/**
*
*/
public static interface BlockListener<K, V> {
public void blockRequested(int block, LHMap2<K, V> map);
}
List<BlockListener<K, V>> listeners = new ArrayList<BlockListener<K, V>>();
// int savedBlocks;
int N;
int level = 0;
int split = 0;
int blockSize;
long totalWrites = 0;
List<Block<K, V>> blockList = new ArrayList<Block<K, V>>();
public void addBlockListener(BlockListener<K, V> listener) {
listeners.add(listener);
}
void notifyBlockRequested(int block) {
for (BlockListener<K, V> l : listeners) {
l.blockRequested(block, this);
}
}
public LHMap2(int blockSize, int nStartingBlocks) {
this.blockSize = blockSize;
this.N = nStartingBlocks;
for (int i = 0; i < nStartingBlocks; ++i) {
addBlock();
}
Runtime.getRuntime().addShutdownHook(new Thread(new Runnable() {
@Override
public void run() {
showStructure();
}
}));
}
public static class Block<K, V> implements Externalizable {
/**
*
*/
int j = 0;
Block<K, V> overflow = null;
LinkedList<K> keyList = new LinkedList<K>();
LinkedList<V> valueList = new LinkedList<V>();
transient private LHMap2<K, V> owner;
transient private Map<K, V> shadow = new TreeMap<K, V>();
private boolean changed = false;
private int size = 0;
public LHMap2<K, V> getOwner() {
return owner;
}
public void setOwner(LHMap2<K, V> owner) {
this.owner = owner;
Block<K, V> ov = overflow;
while (ov != null) {
overflow.setOwner(owner);
ov = ov.overflow;
}
}
public Block() {
super();
}
public Block(LHMap2<K, V> map) {
setOwner(map);
}
public V put(K k, V v) {
setChanged(true);
V v2 = replace(k, v);
if (v2 == null) {
++size;
if (keyList.size() == getOwner().blockSize) {
if (overflow == null) {
getOwner().blockOverflowed(this, k, v);
} else {
overflow.put(k, v);
}
} else {
keyList.addFirst(k);
valueList.addFirst(v);
}
}
return v2;
}
void setChanged(boolean b) {
changed = b;
}
public Map<K, V> drainToMap(Map<K, V> map) {
while (!keyList.isEmpty()) {
K k = keyList.removeLast();
V v = valueList.removeLast();
map.put(k, v);
}
if (overflow != null)
map = overflow.drainToMap(map);
garbageCollectionOverflow();
return map;
}
public void updateMap(Map<K, V> map) {
Iterator<K> ik = keyList.descendingIterator();
Iterator<V> iv = valueList.descendingIterator();
while (ik.hasNext() && iv.hasNext()) {
map.put(ik.next(), iv.next());
}
if (overflow != null)
overflow.updateMap(map);
}
private void garbageCollectionOverflow() {
if (overflow != null) {
overflow.garbageCollectionOverflow();
overflow = null;
}
}
public void addOverflowBucket() {
// assert overflow is needed
if (keyList.size() < getOwner().blockSize)
return;
if (overflow == null) {
overflow = new Block<K, V>(getOwner());
} else {
overflow.addOverflowBucket();
}
}
public V replace(K key, V v2) {
if (overflow != null) {
V v = overflow.replace(key, v2);
if (v != null)
return v;
}
Iterator<K> i = keyList.listIterator();
int j = 0;
while (i.hasNext()) {
if (key.equals(i.next())) {
V v = valueList.get(j);
if (v2 != null) {
valueList.set(j, v2);
}
return v;
}
++j;
}
return null;
}
public boolean isChanged() {
return changed;
}
@Override
public void readExternal(ObjectInput arg0) throws IOException,
ClassNotFoundException {
int sz = arg0.readInt();
for (int i = 0; i < sz; ++i) {
K k = (K) arg0.readObject();
V v = (V) arg0.readObject();
shadow.put(k, v);
}
}
public void loadFromShadow(LHMap2<K, V> owner) {
setOwner(owner);
Block<K, V> b = this;
for (K k : shadow.keySet()) {
if (b.keyList.size() == owner.blockSize) {
Block<K, V> overflow = new Block<K, V>(owner);
b.overflow = overflow;
b = overflow;
}
b.keyList.add(k);
b.valueList.add(shadow.get(k));
}
shadow.clear();
}
@Override
public void writeExternal(ObjectOutput arg0) throws IOException {
if (!changed)
return;
Map<K, V> map = new TreeMap<K, V>();
updateMap(map);
int sz = map.size();
arg0.writeInt(sz);
for (K k : map.keySet()) {
arg0.writeObject(k);
arg0.writeObject(map.get(k));
}
setChanged(false);
}
}
void init() {
for (int i = 0; i < N; ++i) {
addBlock();
}
}
/**
* @param hashValue
* @return a bucket number.
*/
int getDynamicHash(int hashValue) {
long unsignedHash = ((long) hashValue << 32) >>> 32;
// ^^ this long cast needed
int h = (int) (unsignedHash % (N << level));
// System.err.println("h = " + h);
if (h < split) {
h = (int) (unsignedHash % (N << (level + 1)));
// System.err.println("h < split, new h = " + h);
}
return h;
}
@Override
public V put(K k, V v) {
++totalWrites;
int h = getDynamicHash(k.hashCode());
Block<K, V> b = getBlock(h);
b.put(k, v);
return v;
}
public long getTotalWrites() {
return totalWrites;
}
private Block<K, V> getBlock(int h) {
notifyBlockRequested(h);
return blockList.get(h);
}
void blockOverflowed(Block<K, V> b, K k, V v) {
splitNextBucket();
b.addOverflowBucket();
b.put(k, v);
}
private void splitNextBucket() {
Block<K, V> b = getBlock(split);
TreeMap<K, V> map = new TreeMap<K, V>();
b.drainToMap(map);
addBlock();
System.err.printf("split N LEVEL %d %d %d \n", split, N, level);
if (++split >= (N << level)) {
++level;
split = 0;
}
for (K k : map.keySet()) {
V v = map.get(k);
int h = getDynamicHash(k.hashCode());
System.err.println(h + " ");
Block<K, V> b2 = getBlock(h);
b2.put(k, v);
}
}
private Block<K, V> addBlock() {
Block<K, V> b = new Block<K, V>(this);
blockList.add(b);
return b;
}
@Override
public void clear() {
blockList = new ArrayList<Block<K, V>>();
split = 0;
level = 0;
totalWrites = 0;// savedBlocks = 0;
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return values().contains(value);
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
TreeSet<Map.Entry<K, V>> set = new TreeSet<Map.Entry<K, V>>();
Set<K> kk = keySet();
for (K k : kk) {
final K k2 = k;
set.add(new Entry<K, V>() {
@Override
public K getKey() {
return k2;
}
@Override
public V getValue() {
return get(k2);
}
@Override
public V setValue(V value) {
return put(k2, value);
}
});
}
return set;
}
@Override
public V get(Object key) {
int h = getDynamicHash(key.hashCode());
Block<K, V> b = getBlock(h);
return b.replace((K) key, null);
}
@Override
public boolean isEmpty() {
return size() == 0;
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
kk.addAll(b.keyList);
Block<K, V> ov = b.overflow;
while (ov != null) {
kk.addAll(ov.keyList);
ov = ov.overflow;
}
}
return kk;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public V remove(Object key) {
return null;
}
@Override
public int size() {
long sz = longSize();
return (int) (sz > Integer.MAX_VALUE ? Integer.MAX_VALUE
: sz);
}
public long longSize() {
long sz = 0;
for (Block<K, V> b : blockList) {
Block<K, V> b1 = b;
while (b1 != null) {
sz += b1.size;
b1 = b.overflow;
}
}
return sz;
}
@Override
public Collection<V> values() {
ArrayList<V> list = new ArrayList<V>();
Set<K> kk = keySet();
for (K k : kk) {
list.add(get(k));
}
return list;
}
private void showStructure() {
for (int i = 0; i < blockList.size(); ++i) {
Block<K, V> b = getBlock(i);
Block<K, V> ov = b.overflow;
int k = 0;
while (ov != null) {
ov = ov.overflow;
++k;
}
System.out.println("Block " + i + " size " + b.keyList.size()
+ " overflow blocks = " + k);
}
}
}
在此实现中,每个块都是一个文件,因为块在这里是可变大小的,以适应泛型和可变大小的键值对,而溢出块是概念上的,而不是实际的,因为在磁盘存储上,块的内容及其溢出桶(如果有)的内容在此实现中被保存为交替的键和值的列表。在 Block 数据类中实现 Externalizable 接口,使用标准的 Java 自定义对象持久化方法,使用保存和加载到对象流的方法。
package linearhashmap;
import java.io.ByteArrayInputStream;
import java.io.ByteArrayOutputStream;
import java.io.File;
import java.io.FileInputStream;
import java.io.FileNotFoundException;
import java.io.FileOutputStream;
import java.io.IOException;
import java.io.ObjectInputStream;
import java.io.ObjectOutputStream;
import java.io.Serializable;
import java.util.ArrayList;
import java.util.Random;
/**
* This class manages the LHMap2 class block disk swapping, and saves and load an instance of the LHMap2 class.
* It has been used to externally index a legacy file based database of 100,000 record master table, and 1,000,000 record
* sized child tables, and accounts for heap space available in the java virtual machine, so that OutOfMemory errors
* are avoided when the heap space is low by putting blocks back on files, and garbage collecting them.
* The main performance bottleneck appeared when loading a million record table for an index , on initial creation
* of the index.
* @author doctor
*
* @param <K>
* @param <V>
*/
public class LHMap2BlockFileManager<K, V> implements
LHMap2.BlockListener<K, V>, Serializable {
/**
*
*/
private static final long serialVersionUID = 2615265603397988894L;
LHMap2BlockFileManagerData data = new LHMap2BlockFileManagerData(
new byte[10000], new Random(), 0, new ArrayList<Integer>(), 0);
public LHMap2BlockFileManager(File baseDir, String name, int maxBlocks,
double unloadRatio) {
data.home = new File(baseDir, name);
if (!data.home.exists())
data.home.mkdir();
this.data.maxBlocks = maxBlocks;
this.data.unloadRatio = unloadRatio;
}
@Override
public void blockRequested(int block, LHMap2<K, V> map) {
LHMap2.Block<K, V> b = map.blockList.get(block);
if (b == null) {
int tries = 3;
File f = new File(data.home, Integer.toString(block));
do {
if (f.exists())
break;
if (!f.exists()) {
if (--tries >= 0)
fatal(block);
try {
Thread.sleep(100);
} catch (InterruptedException e) {
e.printStackTrace();
}
}
} while (true);
try {
ByteArrayInputStream bis = new ByteArrayInputStream(data.buf);
FileInputStream fis = new FileInputStream(f);
int sz = fis.read(data.buf);
fis.close();
addByteStats(sz);
ObjectInputStream ois = new ObjectInputStream(bis);
b = new LHMap2.Block<K, V>();
b.readExternal(ois);
ois.close();
b.loadFromShadow(map);
map.blockList.set(block, b);
--data.retired;
} catch (FileNotFoundException e) {
e.printStackTrace();
fatal(block);
} catch (IOException e) {
e.printStackTrace();
fatal(block);
} catch (ClassNotFoundException e) {
e.printStackTrace();
fatal(block);
}
}
int size = map.blockList.size();
try {
long freeMemory = Runtime.getRuntime().freeMemory();
long limitMemory = (long) (data.avgBlockSize * data.unloadRatio * size);
if (block % 30 == 0)
System.err.println("free memory =" + freeMemory + " limit "
+ limitMemory);
if (map.split % 20 == 19) {
// this is just to add statistics before really needing to retire
retireRandomBlock(map, block);
++data.retired;
} else if (freeMemory < limitMemory) {
for (int i = 0; i < size / 4; ++i) {
retireRandomBlock(map, block);
++data.retired;
}
System.runFinalization();
System.gc();
}
} catch (FileNotFoundException e) {
e.printStackTrace();
} catch (IOException e) {
e.printStackTrace();
}
}
private void addByteStats(int sz) {
++data.avgCount;
data.avgBlockSize = (int) ((data.avgBlockSize
* (data.avgCount - 1) + sz) / data.avgCount);
}
public void retireRandomBlock(LHMap2<K, V> map, int notThisOne)
throws FileNotFoundException, IOException {
int pick = 0;
int size = map.blockList.size();
LHMap2.Block<K, V> b = null;
for (pick = 0; pick < size
&& (pick == notThisOne || (b = map.blockList.get(pick)) == null); ++pick)
;
if (pick < size)
retireOneBlock(map, pick, b);
}
private void retireOneBlock(LHMap2<K, V> map, int pick, LHMap2.Block<K, V> b)
throws IOException, FileNotFoundException {
if (b == null)
return;
if (b.isChanged()) {
// System.err.println("Retiring " + pick);
File f = new File(data.home, Integer.toString(pick));
ByteArrayOutputStream bos = new ByteArrayOutputStream();
ObjectOutputStream oos = new ObjectOutputStream(bos);
b.writeExternal(oos);
oos.flush();
oos.close();
FileOutputStream fos = new FileOutputStream(f);
byte[] bb = bos.toByteArray();
fos.write(bb);
fos.flush();
fos.close();
if (bb.length > data.buf.length) {
data.buf = bb;
}
}
map.blockList.set(pick, null);
b = null;
}
private void fatal(int block) {
Exception e = new Exception();
try {
throw e;
} catch (Exception e2) {
e2.printStackTrace();
}
System.err.println("block " + block
+ " requested and it is not in blocklist and not a file");
for (int i : data.retirees) {
System.err.print(i + " ");
}
System.err.println(" were retired");
System.exit(-2);
}
public static boolean metaExists(File indexDir, String name) {
File home = new File(indexDir, name);
return new File(home, "LinearMap2").exists();
}
public static <K, V> LHMap2<K, V> load(File baseDir, String name)
throws FileNotFoundException, IOException, ClassNotFoundException {
File home = new File(baseDir, name);
File f2 = new File(home, "LinearMap2");
ObjectInputStream ois = new ObjectInputStream(new FileInputStream(f2));
LHMap2<K, V> map = (LHMap2<K, V>) ois.readObject();
ois.close();
loadBlocks(map);
return map;
}
private static <K, V> void loadBlocks(LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(map);
int size = map.blockList.size();
for (int i = 0; i < size; ++i) {
mgr.blockRequested(i, map);
}
}
public static <K, V> LHMap2BlockFileManager<K, V> getBlockManagerListener(
LHMap2<K, V> map) {
LHMap2BlockFileManager<K, V> mgr = (LHMap2BlockFileManager<K, V>) map.listeners
.get(0);
return mgr;
}
public static void save(File indexDir, String name,
LHMap2<?, ?> offsetMap) throws FileNotFoundException, IOException {
retireAllBlocks(offsetMap);
File home = new File(indexDir, name);
File f2 = new File(home, "LinearMap2");
ObjectOutputStream oos = new ObjectOutputStream(
new FileOutputStream(f2));
oos.writeObject(offsetMap);
oos.close();
}
private static <K, V> void retireAllBlocks(LHMap2<K, V> offsetMap)
throws FileNotFoundException, IOException {
LHMap2BlockFileManager<K, V> mgr = getBlockManagerListener(offsetMap);
int sz = offsetMap.blockList.size();
for (int i = 0; i < sz; ++i) {
LHMap2.Block<K, V> b = offsetMap.blockList.get(i);
// offsetMap.blockList.set(i, null); // mark for reloading as block
// destroyed after writing
if (b != null) {
mgr.retireOneBlock(offsetMap, i, b);
}
}
}
}
package linearhashmap;
import java.io.File;
import java.io.Serializable;
import java.util.List;
import java.util.Random;
public class LHMap2BlockFileManagerData implements Serializable{
/**
*
*/
private static final long serialVersionUID = 1L;
public byte[] buf;
public Random r;
public File baseDir;
public File home;
public int maxBlocks;
public int retired;
public double unloadRatio;
public List<Integer> retirees;
public int avgBlockSize;
public long avgCount;
public LHMap2BlockFileManagerData(byte[] buf, Random r, int retired,
List<Integer> retirees, long avgCount) {
this.buf = buf;
this.r = r;
this.retired = retired;
this.retirees = retirees;
this.avgCount = avgCount;
}
}
- ↑ 最简单的哈希表方案 - “线性探测开放寻址法”,“链地址法”等 - 在最坏情况下具有 O(n) 的查找时间,在这种情况下,大多数键(意外或恶意地)“碰撞” - 大多数键被映射到一个或几个桶。其他哈希表方案 - “布谷鸟哈希”,“动态完美哈希”等 - 即使在最坏情况下也能保证 O(1) 的查找时间。当插入一个新键时,这些方案会在需要时改变其哈希函数以避免冲突。
- ↑ 维基百科:编程语言比较(映射) 显示了多少编程语言提供了哈希表功能。

