数据结构/树
树是一个非空集合,其中一个元素被指定为树的根,而其余元素被划分为非空集合,每个集合都是根的子树。
树节点具有许多有用的属性。节点的深度是从根节点到该节点的路径长度(或边数)。节点的高度是从该节点到其叶子的最长路径。树的高度是根节点的高度。叶子节点没有子节点——它唯一的路径是向上到其父节点。
有关更多信息,请参见树的公理化发展及其结果。
树的类型
二叉树:每个节点有零个、一个或两个子节点。这个断言使许多树操作变得简单和高效。
二叉搜索树:二叉树,其中任何左子节点的值都小于其父节点,任何右子节点的值都大于或等于其父节点的值。
许多问题要求我们以系统的方式访问树的节点:例如,计算存在多少个节点或找到最大元素的任务。二叉树可以使用三种不同的方法:先序、后序和中序,它们都做三件事:递归地遍历左子树和右子树,并访问当前节点。不同之处在于算法何时访问当前节点。
先序:当前节点,左子树,右子树(DLR)
后序:左子树,右子树,当前节点(LRD)
中序:左子树,当前节点,右子树(LDR)
层序:从根节点开始,逐层,从左到右。
- 访问意味着执行一些涉及树中当前节点的操作,例如增加计数器或检查当前节点的值是否大于任何其他记录的值。
preorder(node) visit(node) if node.left ≠ null then preorder(node.left) if node.right ≠ null then preorder(node.right)
inorder(node) if node.left ≠ null then inorder(node.left) visit(node) if node.right ≠ null then inorder(node.right)
postorder(node) if node.left ≠ null then postorder(node.left) if node.right ≠ null then postorder(node.right) visit(node)
levelorder(root) queue<node> q q.push(root) while not q.empty do node = q.pop visit(node) if node.left ≠ null then q.push(node.left) if node.right ≠ null then q.push(node.right)
对于对堆栈压力较小的算法,请参见线程树。
preorder: 50,30, 20, 40, 90, 100 inorder: 20,30,40,50, 90, 100 postorder: 20,40,30,100,90,50
当已经排序的条目存储在树中时,所有新记录都将走相同的路线,并且树看起来更像一个列表(这样的树被称为退化树)。因此,树需要平衡例程,确保所有分支下都有相同数量的记录。这将使树的搜索速度保持在最佳状态。具体来说,如果一个具有n个节点的树是退化树,那么穿过树的最长路径将是 n 个节点;如果它是平衡树,那么最长路径将是log n个节点。
算法/左旋转:这展示了如何应用平衡来在一个Treap中建立优先级堆的不变性,Treap是一种数据结构,它具有堆的排队性能和树的关键查找性能。平衡操作可以改变树结构,同时保持另一个顺序,即二叉树排序顺序。二叉树顺序是从左到右,左节点的键小于右节点的键,而优先级顺序是从上到下,较高节点的优先级大于较低节点的优先级。或者,优先级可以被视为另一个排序键,只是查找特定键更加复杂。
平衡操作可以移动节点上下树,而不会影响左右顺序。
AVL:根据以下规范平衡的二叉搜索树:任何节点的两个子树的高度差最多为一。
红黑树:一个平衡的二叉搜索树,使用基于分配给节点的颜色以及附近节点的颜色来进行平衡算法。
AA 树:一个平衡树,实际上是红黑树的更严格变体。
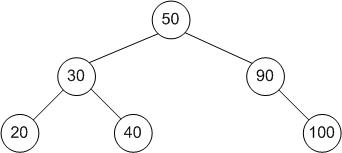
一个典型的二叉搜索树看起来像这样
节点存储在树中的任何项目。根节点树中的顶层项目。(树中上面的 50)子节点当前节点下的节点。(树中上面的 20 和 40 是 30 的子节点)父节点直接在当前节点上方的节点。(树中上面的 90 是 100 的父节点)叶子节点没有子节点的节点。(树中上面的 20 是叶子节点)
要在二叉树中搜索一个项目
- 从根节点开始
- 如果您要搜索的项目小于根节点,则移动到根节点的左子节点;如果您要搜索的项目大于根节点,则移动到根节点的右子节点;如果它等于根节点,那么您已经找到了要查找的项目。
- 现在检查您要搜索的项目是否等于、小于或大于您所在的新的节点。同样,如果您要搜索的项目小于当前节点,则移动到左子节点;如果您要搜索的项目大于当前节点,则移动到右子节点。
- 重复此过程,直到找到要搜索的项目,或者直到节点在正确的分支上没有子节点,在这种情况下,树不包含您要搜索的项目。
例如,要查找节点 40...
- 根节点是 50,它大于 40,因此您转到 50 的左子节点。
- 50 的左子节点是 30,它小于 40,因此您接下来转到 30 的右子节点。
- 30 的右子节点是 40,因此您找到了要查找的项目 :)
.........
- 要添加一个项目,您首先必须遍历树,找到要放置它的位置。您遵循上述步骤进行操作。
- 当您到达一个节点,该节点在正确分支上没有子节点时,就在那里添加新的节点。
例如,要添加节点 25...
- 根节点是 50,它大于 25,因此您转到 50 的左子节点。
- 50 的左子节点是 30,它大于 25,因此您转到 30 的左子节点。
- 30 的左子节点是 20,它小于 25,因此您转到 20 的右子节点。
- 20 的右子节点不存在,因此您在那里添加 25 :)
假设您已经使用上面描述的搜索技术找到了要删除的节点。
例如,要删除 40...
- 只需删除节点!
- 将要删除的节点的子节点直接连接到要删除的节点的父节点。
例如,要删除 90...
- 删除 90,然后使 100 成为 50 的子节点。
一种非标准方法是将节点旋转到选定的子树中,并尝试从该子树中递归地再次删除键,直到出现情况 1 或情况 2。这可能会使树失去平衡,因此随机选择向右旋转还是向左旋转可能会有所帮助。
标准方法是选择左子节点或右子节点,例如右子节点,然后通过从右子节点开始,一直向左移动,直到下一个左为 null,来获取右节点的最左后代。然后移除右子节点的这个最左后代,用其右子树替换它(它的左子节点为 null)。然后使用这个以前右子节点的最左后代的内容,替换要删除的节点的键和值,以便其值现在位于已删除的节点(右子节点的父节点)中。这仍然维护所有节点的键排序。下面是 treap 示例代码中的 Java 代码示例。
以下示例使用标准算法,即后继是待删除节点的右子树中最左边的节点。
例如,要删除 30
- 要删除的节点的右节点是 40。
- (从现在开始,我们一直转到左节点,直到没有另一个节点......)40 的第一个左节点是 35。
- 35 没有左节点,因此 35 是后继者!
- 35 替换 30,位于原始右节点,具有 35 的节点被删除,用其右子树(根节点为 37)替换。
- 直接将待删除节点右侧的子节点移动到待删除节点的位置。
- 由于新节点没有左子节点,您可以将已删除节点的左子树的根节点作为其左子节点。
例如,要删除 30
- 用后继的内容(40)替换要删除的内容(30)。
- 删除后继节点(内容为 40),用其右子树(头部内容为 45)替换它。
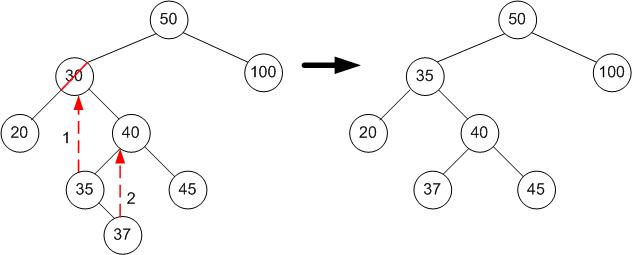
这最好用一个例子来说明
要删除 30...
- 用后继的内容(35)替换要删除的内容(30)。
- 用其右子树(37)替换后继节点(35)。没有左子树,因为后继节点是最左边的。
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del);
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// non-standard method,
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
红黑树是一种自平衡树结构,它为每个节点应用一种颜色。红黑树的结构必须遵守一组规则,这些规则规定了特定颜色节点的排列方式。当树以某种方式修改时,就会应用这些规则,在插入新节点或删除旧节点时,会导致某些节点的旋转和重新着色。这使红黑树保持平衡,保证搜索复杂度为 O(log n)。
红黑树必须遵守的规则如下:
- 每个节点必须是红色或黑色。
- 根节点始终是黑色。
- 树中的所有叶节点都是黑色(叶节点不包含数据,可以在大多数编程语言中建模为null 或nil 引用)。
- 每个红色节点必须有两个黑色子节点。
- 从给定节点到其任何后代叶节点的每条路径必须包含相同数量的黑色节点。
红黑树可以建模为 2-3-4 树,它是 B 树(如下)的子类。带有 1 个红色节点的黑色节点可以看作是链接在一起的 3-节点,带有 2 个红色子节点的黑色节点可以看作是 4-节点。
4-节点被拆分,生成两个节点,中间节点变为红色,这将使中间节点的父节点(没有红色子节点)从 2-节点变为 3-节点,并将带有 1 个红色子节点的父节点变为 4-节点(但这不是总是左红色节点)。
两个红色节点的内联排列被旋转成带有两个红色子节点的父节点,即 4-节点,然后被拆分,如前所述。
A right rotate 'split 4-node' |red
red / \ --> B ---> B
B red/ \red / \
red / \ C A C A
C D / /
D D
Sedgewick 提到的优化是,所有插入的右红色节点都被左旋转,变成左红色节点,因此只有内联的左红色节点需要在拆分之前右旋转。Arne Anderson 在 1993 年的论文中描述的 AA 树(上面)似乎是这种简化的早期阐述,然而他建议使用右倾斜的“红色标记”而不是左倾斜的“红色标记”,正如 Sedgewick 建议的那样,但 AA 树似乎优先于左倾斜的红黑树。如果将来将 Linux CFS 调度程序描述为“基于 AA 的”,那将是一个相当大的冲击。
总之,红黑树是一种检测到同一个侧面的两次插入,并在情况变得更糟之前将树拉平的方法。两次左侧插入将被旋转,两次右侧插入在左旋转以移除右倾斜的红色节点后将看起来像两次左侧插入。同一父节点的两次平衡插入可能会导致 4-节点拆分而无需旋转,因此出现了一个问题,即红黑树是否可以被 a < P < b 的一侧三元组的串行插入攻击,然后是下一个三元组的 P' < a。
以下是 Python 说明代码
RED = 1
BLACK = 0
class Node:
def __init__(self, k, v):
# all newly inserted node's are RED
self.color = RED
self.k = k
self.v = v
self.left = None
self.right = None
class RBTree:
def __init__(self):
self.root = None
def insert(self, k, v) :
self.root = self._insert(self.root, k,v)
def _insert(self, n , k, v):
if n is None:
return Node(k,v)
if k < n.k :
n.left = self._insert(n.left, k , v)
elif k > n.k :
n.right = self._insert(n.right, k, v)
if n.right.color is RED:
#always on the left red's
#left rotate
tmp = n.right
n.right = tmp.left
tmp.left = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.left.color
n.left.color = tmpcolor
if n.left <> None and n.left.left <> None and n.left.left.color == RED and n.left.color == RED:
# right rotate in-line reds
print "right rotate"
tmp = n.left
n.left = tmp.right
tmp.right = n
n = tmp
#color rotation is actually a swap
tmpcolor = n.color
n.color = n.right.color
n.right.color = tmpcolor
if n.left <> None: print n.left.color, n.color, n.right.color
#no need to test, because after right rotation, will need to split 3-node , as right rotation has
#brought red left grandchild to become left red child, and left red child is now red right child
#so there are two red children.
#if n.left <> None and n.right <> None and n.left.color == RED and n.right.color == RED:
print "split"
n.color = RED
n.left.color = BLACK
n.right.color = BLACK
return n
def find(self, k):
return self._find_rb(k, self.root)
def _find_rb(self, k, n):
if n is None:
return None
if k < n.k:
return self._find_rb( k, n.left)
if k > n. k:
return self._find_rb( k, n.right)
return n.v
def inorder(self):
self.inorder_visit(self.root, "O")
def inorder_visit(self, node,label=""):
if node is None: return
self.inorder_visit(node.left, label+"/L")
print label, "val=", node.v
self.inorder_visit(node.right, label+"/R")
def test1(N):
t = RBTree()
for i in xrange(0,N):
t.insert(i,i)
l = []
t.inorder()
for i in xrange(0,N):
x =t.find(i)
if x <> None:
l.append((x, i) )
print "found", len(l)
if __name__ == "__main__":
import random
test1(100000)
test1(1000)
test1(100)
test1(10)
- 二叉树的节点有两个子节点,左子节点及其所有后代小于节点的“值”,右子节点及其所有后代大于节点的“值”,而 B 树是对此的概括。
- 概括是,节点不是一个值,而是一个值列表,列表的大小为 n(n > 2)。n 被选择以优化存储,以便节点的大小对应于一个块,例如。这是在 ssd 驱动器出现之前的年代,但在 ssd ram 上搜索二叉节点仍然比搜索 ssd ram 中的值块,加载到普通 ram 和 cpu 缓存中,然后搜索加载的列表要慢。
- 在列表开头,列表第一个元素的左孩子的值小于第一个元素,其所有孩子也如此。第一个元素的右边是一个孩子,其值大于第一个元素的值,其所有孩子也如此,但也小于第二个元素的值。可以使用归纳法,对于元素 1 和 2 之间的孩子、2 和 3 之间的孩子、... 直到 n-1 和第 n 个节点,都成立。
- 在非满 B 树节点中插入,相当于在排序列表中插入。
- 在 B+ 树中,插入只能在叶子节点进行,非叶子节点包含相邻子节点之间分隔值的副本,例如元素右孩子节点列表中最左边的值。
- 当列表变得满时,例如有 n 个节点,节点会被“分裂”,这意味着创建两个新的节点,并将分隔值传递给父节点。
B 树最初被描述为二叉搜索树的泛化,其中二叉树是 2 节点 B 树,2 代表两个孩子,由 2-1 = 1 个键分隔两个孩子。因此,3 节点有 2 个值分隔 3 个孩子,N 节点有 N 个孩子,由 N-1 个键分隔。
经典的 B 树可以有 N 节点内部节点,以及空 2 节点作为叶子节点,或者更方便地,孩子可以是值或者指向下一个 N 节点的指针,所以它是联合。
B 树的主要思想是,从一个根节点 N 节点开始,它可以保存 N-1 个条目,但在第 N 个条目时,节点的键数用尽,节点可以分裂成两个大小为 N/2 的 N 节点,由单个键 K 分隔,它等于右节点最左边的键,所以任何键 K2 等于或大于 K 的条目都放在右节点,小于 K 的条目都放在左节点。当根节点分裂时,创建一个新的根节点,包含一个键,以及一个左孩子和一个右孩子。由于有 N 个孩子,但只有 N-1 个条目,所以最左边的孩子被存储为一个单独的指针。如果最左边的指针分裂,则左半部分成为新的最左边的指针,右半部分和分隔键被插入到条目的前面。
另一种是 B+ 树,它在数据库系统中最常使用,因为只有值存储在叶子节点中,而内部节点只存储键和指向其他节点的指针,限制了数据值的大小,因为指针的大小。这通常允许具有更多条目的内部节点适合一定的块大小,例如 4K 是常见的物理磁盘块大小。因此,如果 B+ 树内部节点与物理磁盘块对齐,则从磁盘读取大型索引块的主要速率限制因素(因为它没有缓存在内存块列表中)将减少到一次块读取。
B+ 树具有更大的内部节点,因此理论上比等效的 B 树更宽更短,后者必须将所有节点都容纳在给定的物理块大小内,因此总的来说,由于扇出更大,到达键的平均高度更低,因此它是更快的索引。
显然,这种扇出非常重要,压缩也可以应用于块,以增加适合给定底层块大小的条目数量(底层通常是文件系统块)。
大多数数据库系统使用 B+ 树算法,包括 postgresql、mysql、derbydb、firebird、许多 Xbase 索引类型等。
许多文件系统也使用 B+ 树来管理它们的块布局(例如 xfs、NTFS 等)。
Transwiki 有一个 B+ 树的 Java 实现,它使用传统的数组作为键列表和值列表。
下面是一个 B 树的示例,带有测试驱动程序,以及一个 B+ 树,带有测试驱动程序。内存/磁盘管理未包含在内,但在 哈希内存检查示例 中可以找到一个可用的 hack 示例。
这个 B+ 树实现是从 B 树中写出来的,与 transwiki B+ 树的不同之处在于,它试图使用标准 Java 集合库中已存在的 SortedMap 和 SortedSet 的语义。
因此,这个 B+ 实现的扁平叶子块列表不能包含不包含任何数据的块,因为排序依赖于条目的第一个键,所以需要创建一个包含其第一个条目的叶子块。
一个 B 树 Java 示例
[edit | edit source]package btreemap;
import java.util.ArrayList;
import java.util.Collection;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.TreeMap;
/** can't work without setting a comparator */
public class BTreeMap<K, V> implements SortedMap<K, V> {
private static final int NODE_SIZE = 100;
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return comparator;
}
Comparator< ? super K> defaultComparator = new
Comparator< K>() {
@Override
public int compare(K o1, K o2) {
// TODO Auto-generated method stub
Comparable c1 = (Comparable)o1;
Comparable c2 = (Comparable)o2;
return c1.compareTo(c2);
}
};
Comparator<? super K> comparator = defaultComparator;
BTBlock<K, V> root = new BTBlock<K, V>(NODE_SIZE, comparator);
/**
*
* @param comparator
* - this is mandatory for the tree to work
*/
public void setComparator(Comparator<? super K> comparator) {
this.comparator = comparator;
root = new BTBlock<K, V>(NODE_SIZE, comparator);
}
/**
*
*
*
* @param <K>
* @param <V>
* the entry is associated with a right child block.
*
*/
static class BlockEntry<K, V> {
K k;
V v;
BTBlock left;
BlockEntry() {
}
BlockEntry(K k, V v) {
left = null;
this.k = k;
this.v = v;
}
}
/**
*
* - this represents the result of splitting a full block into
* a left block, and a right block, and a median key, the right
* block and the median key held in a BlockEntry structure as above.
* @param <K>
* @param <V>
* @param <V>g
*/
static class SplitRootEntry<K, V> {
BTBlock<K, V> right;
BlockEntry<K, V> entry;
SplitRootEntry(BlockEntry<K, V> entry, BTBlock<K, V> right) {
this.right = right;
this.entry = entry;
}
SplitRootEntry() {
super();
}
}
/**
* this is used to return a result of a possible split , during recursive
* calling.
*
*
*
* @param <K>
* @param <V>
*/
static class resultAndSplit<K, V> {
/**
* null , if there is no split.
*/
SplitRootEntry<K, V> splitNode;
V v;
resultAndSplit(V v) {
this.v = v;
}
resultAndSplit(SplitRootEntry<K, V> entry, V v) {
this.v = v;
this.splitNode = entry;
}
}
/**
* used to represent the insertion point after searching a block if compare
* is zero, then a match was found, and pos is the insertion entry if
* compare < 0 and pos == 0 , then the search ended up less than the
* leftmost entry else compare > 0 , and the search will be to the immediate
* right of pos.
*
*
*
*/
static class PosAndCompare {
int pos = 0;
int compare = 0;
}
static class BTBlock<K, V> {
List<BlockEntry<K, V>> entries;
BTBlock<K, V> rightBlock = null;
private int maxSz = 0;
Comparator<? super K> comparator;
Comparator<? super K> comparator() {
return comparator;
}
public BTBlock(int size, Comparator<? super K> c) {
entries = new ArrayList<BlockEntry<K, V>>();
maxSz = size;
this.comparator = c;
}
/**
* PosAndCompare usage: if compare is zero, then a match was found, and
* pos is the insertion entry if compare < 0 and pos == 0 , then the
* search ended up less than the leftmost entry else compare > 0 , and
* the search will be to the immediate right of pos.
*
*
*
*/
// private void blockSearch(K k, PosAndCompare pc) {
// for (int i = 0; i < entries.size(); ++i) {
// pc.compare = comparator.compare(k, entries.get(i).k);
// if (pc.compare == 0) {
// pc.pos = i;
// return;
// }
// if (pc.compare < 0 && i == 0) {
// pc.pos = 0;
// return;
// }
//
// if (pc.compare < 0) {
// pc.pos = i - 1;
// pc.compare = 1;
// return;
// }
//
// }
// pc.pos = entries.size() - 1;
// pc.compare = 1;
//
// // binary search, it's hard to get it right !
// // int left = 0;
// // int right = entries.size();
// //
// // while (left <= right && left < entries.size()) {
// // // pc.pos = (right - left) / 2 + left;
// // pc.pos = (left + right) / 2;
// // pc.compare = comparator().compare(k, entries.get(pc.pos).k);
// // if (pc.compare < 0) {
// // right = pc.pos - 1;
// // } else if (pc.compare > 0) {
// // left = pc.pos + 1;
// // } else {
// // return;
// // }
// // }
// //
// // BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
// // pc.pos = Collections.binarySearch(entries, e, cmp);
//
// }
Comparator<BlockEntry<K, V>> cmp = new Comparator<BlockEntry<K, V>>() {
@Override
public int compare(BlockEntry<K, V> o1, BlockEntry<K, V> o2) {
// TODO Auto-generated method stub
return comparator.compare(o1.k, o2.k);
}
};
resultAndSplit<K, V> put(K k, V v) {
V v2;
if (entries.size() == 0) {
entries.add(new BlockEntry<K, V>(k, v));
return new resultAndSplit<K, V>(v);
} else {
// PosAndCompare pc = new PosAndCompare();
BlockEntry<K, V> e = new BlockEntry<K, V>(k, v);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
// blockSearch(k, pc);
// a match
if (res >= 0) {
v2 = entries.get(res).v;
entries.get(res).v = v;
return new resultAndSplit<K, V>(v2);
}
// follow leftBlock if search is to left of first entry
if (index == entries.size() && rightBlock != null) {
resultAndSplit<K, V> result = rightBlock.put(k, v);
if (result.splitNode != null) {
rightBlock = result.splitNode.right;
entries.add(result.splitNode.entry);
}
} else if (index == entries.size() && rightBlock == null
&& entries.size() == maxSz) {
rightBlock = new BTBlock<K, V>(this.maxSz, comparator);
resultAndSplit<K, V> result = rightBlock.put(k, v);
} else if (index < entries.size()
&& entries.get(index).left != null) {
// follow right block if it exists
resultAndSplit<K, V> result = entries.get(index).left.put(
k, v);
if (result.splitNode != null) {
entries.get(index).left = result.splitNode.right;
// add to the left
entries.add(index, result.splitNode.entry);
}
} else {
// add to the left
entries.add(index, e);
}
// check if overflowed block , split if it has.
if (entries.size() > maxSz) {
int mid = entries.size() / 2;
// copy right half to new entries list.
List<BlockEntry<K, V>> leftEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = 0; i < mid; ++i) {
leftEntries.add(entries.get(i));
}
BlockEntry<K, V> centreEntry = entries.get(mid);
BTBlock<K, V> leftBlock = new BTBlock<K, V>(maxSz,
comparator);
leftBlock.entries = leftEntries;
// the median entry's left block is the new left block's
// leftmost block
leftBlock.rightBlock = centreEntry.left;
// the new right block becomes the right block
centreEntry.left = leftBlock;
// reduce the old block's entries into its left half of
// entries.
ArrayList<BlockEntry<K, V>> newEntries = new ArrayList<BlockEntry<K, V>>();
for (int i = mid + 1; i < entries.size(); ++i)
newEntries.add(entries.get(i));
this.entries = newEntries;
// create a return object, with the reduced old block as the
// left block
// and the median entry with the new right block attached
SplitRootEntry<K, V> split = new SplitRootEntry<K, V>(
centreEntry, this);
// the keyed value didn't exist before , so null
return new resultAndSplit<K, V>(split, null);
}
return new resultAndSplit<K, V>(v);
}
}
V get(K k) {
if (entries.size() == 0)
return null;
BlockEntry<K, V> e = new BlockEntry<K, V>(k, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
if (res >= 0) {
return entries.get(res).v;
}
if (index == entries.size() && rightBlock != null) {
return rightBlock.get(k);
} else if (index < entries.size()
&& entries.get(index).left != null) {
return (V) entries.get(index).left.get(k);
} else
return null;
}
void getRange(SortedMap map, K k1, K k2) {
BlockEntry<K, V> e = new BlockEntry<K, V>(k1, null);
int res = Collections.binarySearch(entries, e, cmp);
int index = -res - 1;
BlockEntry<K, V> e2 = new BlockEntry<K, V>(k2, null);
int res2 = Collections.binarySearch(entries, e2, cmp);
int index2 = -res2 - 1;
int from = res >= 0 ? res : index;
int to = res2 >= 0 ? res2 : index2;
for (int i = from; i <= to; ++i) {
if (i < entries.size() && (i > from || res < 0)
&& entries.get(i).left != null) {
entries.get(i).left.getRange(map, k1, k2);
// if (pc2.pos == pc.pos)
// break;
}
if (i < to || res2 >= 0)
map.put(entries.get(i).k, entries.get(i).v);
if (i == entries.size() && rightBlock != null) {
rightBlock.getRange(map, k1, k2);
}
}
}
K headKey() {
if (rightBlock != null) {
return rightBlock.headKey();
}
return entries.get(0).k;
}
K tailKey() {
int i = entries.size() - 1;
if (entries.get(i).left != null) {
return (K) entries.get(i).left.tailKey();
}
return entries.get(i).k;
}
void show(int n) {
showTabs(n);
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
System.err.print("#" + i + ":(" + e.k + ":" + e.v + ") ");
}
System.err.println();
showTabs(n);
if (rightBlock != null) {
System.err.print("Left Block\n");
rightBlock.show(n + 1);
} else {
System.err.println("No Left Block");
}
for (int i = 0; i < entries.size(); ++i) {
BlockEntry<K, V> e = entries.get(i);
showTabs(n);
if (e.left != null) {
System.err.println("block right of #" + i);
e.left.show(n + 1);
} else {
System.err.println("No block right of #" + i);
}
}
showTabs(n);
System.err.println("End of Block Info\n\n");
}
private void showTabs(int n) {
// TODO Auto-generated method stub
for (int i = 0; i < n; ++i) {
System.err.print(" ");
}
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
root.getRange(map, fromKey, toKey);
return map;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
// TODO Auto-generated method stub
return subMap(root.headKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
// TODO Auto-generated method stub
return subMap(fromKey, root.tailKey());
}
@Override
public K firstKey() {
// TODO Auto-generated method stub
return root.headKey();
}
@Override
public K lastKey() {
// TODO Auto-generated method stub
return root.tailKey();
}
@Override
public int size() {
// TODO Auto-generated method stub
return 0;
}
@Override
public boolean isEmpty() {
// TODO Auto-generated method stub
return false;
}
@Override
public boolean containsKey(Object key) {
// TODO Auto-generated method stub
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
// TODO Auto-generated method stub
return false;
}
@Override
public V get(Object key) {
// TODO Auto-generated method stub
return root.get((K) key);
}
@Override
public V put(K key, V value) {
resultAndSplit<K, V> b = root.put(key, value);
if (b.splitNode != null) {
root = new BTBlock<K, V>(root.maxSz, root.comparator);
root.rightBlock = b.splitNode.right;
root.entries.add(b.splitNode.entry);
}
return b.v;
}
@Override
public V remove(Object key) {
// TODO Auto-generated method stub
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
// TODO Auto-generated method stub
}
@Override
public void clear() {
// TODO Auto-generated method stub
}
@Override
public Set<K> keySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
public class TestBtree {
private static final int N = 50000;
public static void main(String[] args) {
BTreeMap<Integer, Integer> map = new BTreeMap<Integer , Integer>();
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
map.setComparator(comparator);
List<Integer> testVals = new ArrayList<Integer>();
for (int i =0 ; i < N ; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i ) {
int x = r.nextInt(testVals.size());
x = testVals.remove(x);
//int x=i;
t.add(x);
map.put(x, x);
}
System.err.println("output " + N + " vals");
map.root.show(0);
for (int i = 0; i < N; ++i) {
int x = t.get(i);
if ( x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("Checked " + N + " entries");
}
}
一个 B+ 树 Java 示例
[edit | edit source]实验包括计时运行(例如 time java -cp . btreemap.BPlusTreeTest1),使用外部块大小 + 1 大小的叶子块大小,这样它基本上只是底层的条目 TreeMap,与,例如,400 个内部节点大小,以及 200 个外部节点大小。其他实验包括使用 SkipListMap 代替 TreeMap。
package btreemap;
import java.util.Collection;
import java.util.Comparator;
import java.util.Map;
import java.util.Set;
import java.util.SortedMap;
import java.util.SortedSet;
import java.util.TreeMap;
import java.util.TreeSet;
/**
* a B+ tree, where leaf blocks contain key-value pairs and
* internal blocks have keyed entries pointing to other internal blocks
* or leaf blocks whose keys are greater than or equal to the associated key.
*
* @author syan
*
* @param <K> key type implements Comparable
* @param <V> value type
*/
public class BPlusTreeMap<K, V> implements SortedMap<K, V> {
private int maxInternalBlockSize;
BPlusAnyBlock<K, V> root;
private int maxExternalSize;
BPlusTreeMap(int maxInternalSize, int maxExternalSize) {
this.maxInternalBlockSize = maxInternalSize;
this.maxExternalSize = maxExternalSize;
}
static class SplitOrValue<K, V> {
V v;
K k;
BPlusAnyBlock<K, V> left, right;
boolean split;
public boolean isSplit() {
return split;
}
public void setSplit(boolean split) {
this.split = split;
}
public SplitOrValue(V value) {
v = value;
setSplit(false);
}
public SplitOrValue(BPlusAnyBlock<K, V> left2,
BPlusAnyBlock<K, V> bPlusBlock) {
left = left2;
right = bPlusBlock;
k = right.firstKey();
setSplit(true);
// System.err.printf("\n\n** split occured %s**\n\n", bPlusBlock
// .getClass().getSimpleName());
}
}
static abstract class BPlusAnyBlock<K, V> {
public abstract SplitOrValue<K, V> put(K k, V v);
abstract SplitOrValue<K, V> splitBlock();
public abstract V get(K k);
public abstract boolean isEmpty();
public abstract K firstKey();
}
SortedSet<BPlusLeafBlock<K, V>> blockList = getLeafBlockSet();
SortedSet<BPlusLeafBlock<K, V>> getLeafBlockSet() {
// return new ConcurrentSkipListSet<BPlusLeafBlock<K, V>>();
return new TreeSet<BPlusLeafBlock<K, V>>();
}
static class BPlusLeafBlock<K, V> extends BPlusAnyBlock<K, V> implements
Comparable<BPlusLeafBlock<K, V>> {
SortedMap<K, V> entries = getEntryCollection();
static <K, V> SortedMap<K, V> getEntryCollection() {
return new TreeMap<K, V>();
}
int maxSize;
private BPlusTreeMap<K, V> owner;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusLeafBlock(BPlusTreeMap<K, V> bPlusTreeMap,
SortedMap<K, V> rightEntries) {
this.owner = bPlusTreeMap;
maxSize = owner.maxExternalSize;
entries = rightEntries;
}
public SplitOrValue<K, V> put(K k, V v) {
V v2 = entries.put(k, v);
if (entries.size() >= maxSize)
return splitBlock();
else
return new SplitOrValue<K, V>(v2);
}
public SplitOrValue<K, V> splitBlock() {
SortedMap<K, V> leftEntries = getEntryCollection();
SortedMap<K, V> rightEntries = getEntryCollection();
int i = 0;
for (Entry<K, V> e : entries.entrySet()) {
// System.out.println(this.getClass().getSimpleName() +
// " split entry " + e.getKey());
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
rightEntries.put(e.getKey(), e.getValue());
}
BPlusLeafBlock<K, V> right = createBlock(rightEntries);
// System.out.println("finished block split");
// System.out.println("\nleft block");
// for (K ik : leftEntries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\nright block");
// for (K ik : right.entries.keySet()) {
// System.out.print(ik + " ");
// }
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private BPlusLeafBlock<K, V> createBlock(SortedMap<K, V> rightEntries) {
return owner.createLeafBlock(rightEntries);
}
@Override
public V get(K k) {
return entries.get(k);
}
@Override
public int compareTo(BPlusLeafBlock<K, V> o) {
return ((Comparable<K>) entries.firstKey()).compareTo(o.entries
.firstKey());
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
static class BPlusBranchBlock<K, V> extends BPlusAnyBlock<K, V> {
SortedMap<K, BPlusAnyBlock<K, V>> entries = createInternalBlockEntries();
int maxSize;
private BPlusAnyBlock<K, V> left;
public boolean isEmpty() {
return entries.isEmpty();
}
public BPlusBranchBlock(int maxSize2) {
this.maxSize = maxSize2;
}
public SplitOrValue<K, V> put(K k, V v) {
BPlusAnyBlock<K, V> b = getBlock(k);
SplitOrValue<K, V> sv = b.put(k, v);
if (sv.isSplit()) {
entries.put(sv.k, sv.right);
if (entries.size() >= maxSize)
sv = splitBlock();
else
sv = new SplitOrValue<K, V>(null);
}
return sv;
}
BPlusAnyBlock<K, V> getBlock(K k) {
assert (entries.size() > 0);
BPlusAnyBlock<K, V> b = entries.get(k);
if (b == null) {
// headMap returns less than k
SortedMap<K, BPlusAnyBlock<K, V>> head = entries.headMap(k);
if (head.isEmpty()) {
b = left;
// System.out.println("for key " + k
// + " getting from leftmost block");
// showEntries();
} else {
b = entries.get(head.lastKey());
// System.out.println("for key " + k
// + " getting from block with key " + head.lastKey());
// showEntries();
}
}
assert (b != null);
return b;
}
public void showEntries() {
System.out.print("entries = ");
for (K k : entries.keySet()) {
System.out.print(k + " ");
}
System.out.println();
}
public SplitOrValue<K, V> splitBlock() {
Set<Entry<K, BPlusAnyBlock<K, V>>> ee = entries.entrySet();
int i = 0;
BPlusBranchBlock<K, V> right = new BPlusBranchBlock<K, V>(maxSize);
SortedMap<K, BPlusAnyBlock<K, V>> leftEntries = createInternalBlockEntries();
for (Entry<K, BPlusAnyBlock<K, V>> e : ee) {
// System.out.print("split check " + e.getKey() + ":"
// );
if (++i <= maxSize / 2)
leftEntries.put(e.getKey(), e.getValue());
else
right.entries.put(e.getKey(), e.getValue());
}
// System.out.println("\n");
this.entries = leftEntries;
return new SplitOrValue<K, V>(this, right);
}
private SortedMap<K, BPlusAnyBlock<K, V>> createInternalBlockEntries() {
return new TreeMap<K, BPlusAnyBlock<K, V>>();
}
@Override
public V get(K k) {
BPlusAnyBlock<K, V> b = getBlock(k);
return b.get(k);
}
@Override
public K firstKey() {
return entries.firstKey();
}
}
@Override
public SortedMap<K, V> subMap(K fromKey, K toKey) {
TreeMap<K, V> map = new TreeMap<K, V>();
BPlusLeafBlock<K, V> b1 = getLeafBlock(fromKey);
BPlusLeafBlock<K, V> b2 = getLeafBlock(toKey);
SortedSet<BPlusLeafBlock<K, V>> range = blockList.subSet(b1, b2);
for (BPlusLeafBlock<K, V> b : range) {
SortedMap<K, V> m = b.entries.subMap(fromKey, toKey);
map.putAll(m);
}
return map;
}
private BPlusLeafBlock<K, V> getLeafBlock(K key) {
BPlusAnyBlock<K, V> b1;
b1 = root;
while (b1 instanceof BPlusBranchBlock<?, ?>) {
b1 = ((BPlusBranchBlock<K, V>) b1).getBlock(key);
}
return (BPlusLeafBlock<K, V>) b1;
}
public BPlusLeafBlock<K, V> createLeafBlock(SortedMap<K, V> rightEntries) {
BPlusLeafBlock<K, V> b = new BPlusLeafBlock<K, V>(this, rightEntries);
blockList.add(b);
return b;
}
@Override
public SortedMap<K, V> headMap(K toKey) {
return subMap(firstKey(), toKey);
};
@Override
public SortedMap<K, V> tailMap(K fromKey) {
return subMap(fromKey, lastKey());
}
@Override
public K firstKey() {
return blockList.first().entries.firstKey();
}
@Override
public K lastKey() {
return blockList.last().entries.lastKey();
}
@Override
public int size() {
return (int) getLongSize();
}
private long getLongSize() {
long i = 0;
for (BPlusLeafBlock<K, V> b : blockList) {
i += b.entries.size();
}
return i;
}
@Override
public boolean isEmpty() {
return root.isEmpty();
}
@Override
public boolean containsKey(Object key) {
return get(key) != null;
}
@Override
public boolean containsValue(Object value) {
return false;
}
@Override
public V get(Object key) {
return (V) root.get((K) key);
}
@Override
public V put(K key, V value) {
if (root == null) {
SortedMap<K, V> entries = BPlusLeafBlock.getEntryCollection();
entries.put(key, value);
root = createLeafBlock(entries);
return null;
}
SplitOrValue<K, V> result = root.put(key, value);
if (result.isSplit()) {
BPlusBranchBlock<K, V> root = new BPlusBranchBlock<K, V>(
maxInternalBlockSize);
root.left = result.left;
root.entries.put(result.k, result.right);
this.root = root;
}
return result.v;
}
@Override
public V remove(Object key) {
return null;
}
@Override
public void putAll(Map<? extends K, ? extends V> m) {
for (K k : m.keySet()) {
put(k, m.get(k));
}
}
@Override
public void clear() {
}
@Override
public Set<K> keySet() {
TreeSet<K> kk = new TreeSet<K>();
for (BPlusLeafBlock<K, V> b : blockList) {
kk.addAll(b.entries.keySet());
}
return kk;
}
@Override
public Collection<V> values() {
// TODO Auto-generated method stub
return null;
}
@Override
public Set<java.util.Map.Entry<K, V>> entrySet() {
// TODO Auto-generated method stub
return null;
}
@Override
public Comparator<? super K> comparator() {
// TODO Auto-generated method stub
return null;
}
public void showLeaves() {
for (BPlusLeafBlock<K, V> b : blockList) {
System.out.println("Block");
for (Entry<K, V> e : b.entries.entrySet()) {
System.out.print(e.getKey() + ":" + e.getValue() + " ");
}
System.out.println();
}
}
}
package btreemap;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.List;
import java.util.Random;
/** driver program to test B+ tree */
public class BPlusTreeTest1 {
private static final int N = 1200000;
public static void main(String[] args) {
BPlusTreeMap<Integer, Integer> map = new BPlusTreeMap<Integer, Integer>(
400, 200 );// 5000002);
Random r = new Random();
ArrayList<Integer> t = new ArrayList<Integer>();
Comparator<Integer> comparator = new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
// TODO Auto-generated method stub
return o1.intValue() - o2.intValue();
}
};
List<Integer> testVals = new ArrayList<Integer>();
for (int i = 0; i < N; ++i) {
testVals.add(i);
}
for (int i = 0; i < N; ++i) {
int x = r.nextInt(N);
int z = testVals.set(x, testVals.get(0));
testVals.set(0, z);
}
for (int i = 0; i < N; ++i) {
map.put(testVals.get(i), testVals.get(i));
showProgress("put", testVals, i);
}
System.err.println("output " + N + " vals");
try {
for (int i = 0; i < N; ++i) {
showProgress("get", testVals, i);
int x = testVals.get(i);
if (x != map.get(x))
System.err.println("Expecting " + x + " got " + map.get(x));
}
System.err.println("\nChecked " + N + " entries");
} catch (Exception e) {
// TODO: handle exception
e.printStackTrace();
map.showLeaves();
}
}
private static void showProgress(String label, List<Integer> testVals, int i) {
if (i % (N / 1000) == 0) {
System.out.printf("%s %d:%d; ", label, i, testVals.get(i));
if (i % (N / 10100) == 0)
System.out.println();
}
}
}
Treaps
[edit | edit source]二叉树中的不变式是,左边的键小于右边的键。例如,对于具有顺序的键,ord(L) < ord(R)。然而,这并没有规定节点之间的关系,并且左右旋转不会影响以上内容。因此,可以强加另一种顺序。如果顺序是随机的,它很可能会抵消普通二叉树的任何倾斜,例如,当按顺序插入已经排序的输入时。
下面是一个 Java 示例实现,包括一个普通二叉树删除代码示例。
import java.util.Iterator;
import java.util.LinkedList;
import java.util.Random;
public class Treap1<K extends Comparable<K>, V> {
public Treap1(boolean test) {
this.test = test;
}
public Treap1() {}
boolean test = false;
static Random random = new Random(System.currentTimeMillis());
class TreapNode {
int priority = 0;
K k;
V val;
TreapNode left, right;
public TreapNode() {
if (!test) {
priority = random.nextInt();
}
}
}
TreapNode root = null;
void insert(K k, V val) {
root = insert(k, val, root);
}
TreapNode insert(K k, V val, TreapNode node) {
TreapNode node2 = new TreapNode();
node2.k = k;
node2.val = val;
if (node == null) {
node = node2;
} else if (k.compareTo(node.k) < 0) {
node.left = insert(k, val, node.left);
} else {
node.right = insert(k, val, node.right);
}
if (node.left != null && node.left.priority > node.priority) {
// left rotate
TreapNode tmp = node.left;
node.left = node.left.right;
tmp.right = node;
node = tmp;
} else if (node.right != null && node.right.priority > node.priority) {
// right rotate
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
}
return node;
}
V find(K k) {
return findNode(k, root);
}
private V findNode(K k, Treap1<K, V>.TreapNode node) {
if (node == null)
return null;
if (k.compareTo(node.k) < 0) {
return findNode(k, node.left);
} else if (k.compareTo(node.k) > 0) {
return findNode(k, node.right);
} else {
return node.val;
}
}
static class Deleted {
boolean success = false;
}
boolean delete(K k) {
Deleted del = new Deleted();
root = deleteNode(k, root, del);
return del.success;
}
private Treap1<K, V>.TreapNode deleteNode(K k, Treap1<K, V>.TreapNode node, Deleted del) {
if (node == null) {
return null;
} else if (k.compareTo(node.k) < 0) {
node.left = deleteNode(k, node.left, del) ;
} else if (k.compareTo(node.k) > 0) {
node.right = deleteNode(k, node.right, del);
// k.compareTo(node.k) == 0
} else if ( node.left == null ) {
del.success = true;
return node.right;
} else if ( node.right == null) {
del.success = true;
return node.left;
} else if (node.left !=null && node.right != null){
/*
// left rotate and all delete on left subtree
TreapNode tmp = node.right;
node.right = node.right.left;
tmp.left = node;
node = tmp;
node.left = deleteNode(k , node.left, del);
*/
// more standard method ? doesn't disturb tree structure as much
// find leftmost descendant of the right child node and replace contents
TreapNode n2 = node.right;
TreapNode previous2 = null;
while (n2.left != null) {
previous2 = n2;
n2 = n2.left;
}
if (previous2 != null) {
previous2.left = n2.right;
//n2 has no parent link, orphaned
} else {
node.right = n2.right;
//n2 has no parent link, orphaned
}
node.k = n2.k;
node.val = n2.val;
del.success = true;
// once n2 out of scope, the orphaned node at n2 will be garbage collected,
}
return node;
}
public static void main(String[] args) {
LinkedList<Integer> dat = new LinkedList<Integer>();
for (int i = 0; i < 15000; ++i) {
dat.add(i);
}
testNumbers(dat, true); // no random priority balancing
testNumbers(dat, false);
}
private static void testNumbers(LinkedList<Integer> dat,
boolean test) {
Treap1<Integer, Integer> treap = new Treap1<>(test);
for (Integer integer : dat) {
treap.insert(integer, integer);
}
long t1 = System.currentTimeMillis();
Iterator<Integer> desc = dat.iterator();
int found = 0;
while (desc.hasNext()) {
Integer j = desc.next();
Integer i = treap.find(j);
if (j.equals(i)) {
++found;
}
}
long t2 = System.currentTimeMillis();
System.out.println("found = " + found + " in " + (t2 - t1));
System.out.println("test delete");
int deleted = 0;
for (Integer integer : dat) {
if (treap.delete(integer))
++deleted;
}
System.out.println("Deleted = " + deleted);
}
}
参考文献
[edit | edit source]- William Ford 和 William Tapp。使用STL的C++数据结构。第 2 版。新泽西州上鞍河:普伦蒂斯·霍尔,2002 年。