离散数学/集合论

离散数学
← 简介	集合论	集合论/第 2 页 →

维基百科在 集合论 有相关信息

简介

集合论从最简单的概念开始：它考察一个对象是否属于或不属于一个集合，该集合以某种明确的方式描述了一组对象。从这个简单的开始，可以发展出一系列越来越复杂（而且有用！）的概念，这些概念最终会引申出具有多种应用的符号和技巧。

定义：集合

集合的当前定义可能听起来很模糊。一个集合可以定义为实体的无序集合，这些实体因为符合某个规则而关联在一起。

'实体'可以是任何东西，从字面上讲：数字、人、形状、城市、文本片段，... 等等

关于它们都遵循的'规则'的关键事实是它必须是明确定义的。换句话说，它必须清楚地描述实体遵循的规则。例如，如果我们谈论的是单词，一个明确定义的规则是

X is English

一个未明确定义的规则（因此不能用来定义集合）可能是

X is hard to spell

其中 X 是任何单词

元素

属于给定集合的实体称为该集合的元素。例如

Henry VIII is an element of the set of Kings of England. : kings of England {Henry VIII}

集合符号

要列出集合的元素，我们将它们用花括号括起来，并用逗号隔开。例如

 $\{-3,-2,-1,0,1,2,3\}$

集合的元素也可以用文字描述

 $\{{\text{ integers between }}-3{\text{ and  }}3{\text{ inclusive}}\}$

集合生成器符号可用于描述那些显式列出太繁琐的集合。要表示任何特定的集合，我们使用字母 $x$

 $\{x|x{\text{ is an integer and }}|x|<4\}$

或等效地

 $\{x|x\in \mathbb {Z} ,|x|<4\}$

符号 $\in$ 和 $\notin$ 分别表示元素的包含和排除

 ${\text{dog }}\in \{{\text{quadrupeds}}\}$ 
 ${\text{Washington DC}}\notin \{{\text{European capital cities}}\}$

集合可以包含无限多个元素，例如素数集合。省略号用于表示模式的无限延续

 $\{2,3,5,7,11,\dots \}$

请注意，省略号的使用可能会导致歧义，上面的集合可以看作是可被 4 整除的整数集合，例如。

集合通常用大写字母表示： $A$ , $B$ , ...
元素通常用小写字母表示： $x$ , $y$ , ...

特殊集合

全集

当前上下文中所有实体的集合称为全集，或简称为宇宙。它用 $U$ 表示。

例如，上下文可能是一道作业练习，其中全集被限制为其所考虑的特定实体。同样，它也可能是一道任意问题，我们清楚地知道它应用于何处。

空集

不包含任何元素的集合称为空集或空集。它用一对空括号表示： $\{\}$ 或符号 $\varnothing$ 表示。

定义一个不包含任何元素的集合可能看起来很奇怪。但是，请记住，人们可能正在寻找问题的解决方案，而这些解决方案是否存在尚不清楚。如果事实证明没有解决方案，那么解决方案集就是空的。

例如

如果 $U=\{{\text{words in the English language}}\}$ ，那么 $\{{\text{words with more than 50 letters}}\}=\varnothing$ 。

如果 $U=\{{\text{whole numbers}}\}$ ，那么 $\{x|x^{2}=10\}=\varnothing$ 。

空集上的运算

对空集执行的运算（作为要进行运算的一组事物）也可能令人困惑。（此类运算为空运算。）例如，空集元素的总和为零，但空集元素的乘积为一（见空积）。这可能看起来很奇怪，因为空集没有元素，那么它们加起来或乘起来是否重要？（因为“它们”不存在？）最终，这些运算的结果更多地反映了所讨论的运算，而不是空集本身。例如，请注意零是加法的单位元，而一是乘法的单位元。

特殊的数字集合

一些集合使用频率很高，因此被赋予了特殊的符号。

自然数

从 1 开始的“计数”数（或整数）称为自然数。此集合有时用N 表示。所以N = {1, 2, 3, ...}。

请注意，当我们用手写此集合时，我们无法用粗体类型写入，因此我们用黑板粗体字体写入 N： $\mathbb {N}$

整数

所有整数，正数、负数和零构成整数集合。它有时用Z 表示。所以Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}。

在黑板粗体中，它看起来像这样： $\mathbb {Z}$

实数

如果我们将整数集合扩展到包括所有小数，我们将构成实数集合。实数集合有时用R 表示。

实数的小数点后可能具有有限个数字（例如 3.625），或者具有无限个小数数字。在无限个数字的情况下，这些数字可能是

循环的；例如 8.127127127...

... 或者它们可能不循环；例如 3.141592653...

在黑板粗体中： $\mathbb {R}$

有理数

小数位数有限或循环的那些实数称为有理数。有理数集合有时用字母Q 表示。

有理数总是可以写成精确的p/q 分数；其中p 和q 是整数。如果q 等于 1，则分数只是整数p。请注意，q 不能等于零，因为该值将是未定义的。

例如：0.5、-17、2/17、82.01、3.282828... 都是有理数。

在黑板粗体中： $\mathbb {Q}$

无理数

如果一个数字不能用分数p/q精确地表示，则称该数字为无理数。

例如：√2，√3，π。

集合论练习 1

点击链接查看集合论练习 1

集合之间的关系

现在我们将研究集合之间各种关系。

相等

两个集合 $A$ 和 $B$ 被称为相等，当且仅当它们具有完全相同的元素。在这种情况下，我们简单地写

 $A=B$

注意关于相等集合的另外两个事实

元素的顺序无关紧要。

如果一个元素被列出多次，则忽略任何重复出现的元素。

因此，例如，以下集合都是相等的

 $\{1,2,3\}=\{3,2,1\}=\{1,1,2,3,2,2\}$

(您可能想知道为什么有人会写出像 $\{1,1,2,3,2,2\}$ 这样的集合。您可能还记得，当我们定义空集时，我们注意到可能没有特定问题的解决方案 - 因此需要一个空集。好吧，这里我们可能正在尝试几种不同的解决问题的方法，其中一些实际上导致了相同的解决方案。但是，当我们考虑不同的解决方案时，任何这样的重复将被忽略。）

子集

如果集合 $A$ 的所有元素也是集合 $B$ 的元素，那么我们说 $A$ 是 $B$ 的子集，我们写成

 $A\subseteq B$

例如

在下面的例子中

If  $T=\{2,4,6,8,10\}$  and  $E=\{{\text{even integers}}\}$ , then  $T\subseteq E$ 
If  $A=\{{\text{alphanumeric characters}}\}$  and  $P=\{{\text{printable characters}}\}$ , then  $A\subseteq P$ 
If  $Q=\{{\text{quadrilaterals}}\}$  and  $F=\{{\text{plane figures bounded by four straight lines}}\}$ , then  $Q\subseteq F$

请注意 $A\subseteq B$ 并不意味着 $B$ 必须包含不在 $A$ 中的额外元素；这两个集合可能是相等的 - 就像上面 $Q$ 和 $F$ 一样。但是，如果另外 $B$ 确实包含至少一个不在 $A$ 中的元素，那么我们说 $A$ 是 $B$ 的真子集。在这种情况下，我们将写

 $A\subset B$

在上面的例子中

 $E$  contains ... -4, -2, 0, 2, 4, 6, 8, 10, 12, 14, ... , so  $T\subset E$

 $P$  contains $, ;, &, ..., so  $A\subset P$

但 $Q$ 和 $F$ 只是说同一件事的不同方式，所以 $Q=F$

使用 $\subset$ 和 $\subseteq$ ；与使用 < 和 ≤ 来比较两个数字显然是类似的。

还要注意，每个集合都是全集的子集，而空集是每个集合的子集。

（你可能对最后一个陈述感到好奇：空集怎么能是任何东西的子集，因为它不包含任何元素？这里关键在于，对于每个集合 $A$ ，空集不包含任何不在 $A$ 中的元素。所以 $\oslash \subseteq A$ 对于所有集合 $A$ ）。

最后，请注意，如果 $A\subseteq B{\text{ and }}B\subseteq A{\text{ then }}A$ 和 $B$ 必须包含完全相同的元素，因此相等。换句话说

 $A\subseteq B{\text{ and }}B\subseteq A{\text{ then }}A=B$

不相交

如果两个集合没有共同的元素，则称它们是不相交的。例如

If  $A=\{{\text{even numbers}}\}$  and  $B=\{1,3,5,11,19\}$ , then  $A$  and  $B$  are disjoint sets

韦恩图

韦恩图可以是说明集合之间关系的一种有用方法。

在韦恩图中

全集用一个矩形表示。矩形内的点表示属于全集的元素；矩形外的点表示不属于全集的元素。那么，你可以将这个矩形看作一个“篱笆”，它将不需要的东西拒之门外，并将我们的注意力集中在我们正在讨论的事情上。

其他集合用循环表示，通常呈椭圆形或圆形，绘制在矩形内。同样，给定循环内的点表示它所代表的集合中的元素；循环外的点表示不属于该集合的元素。

在左边，集合A和B是不相交的，因为循环没有重叠。

在右边，A是B的子集，因为代表集合A的循环完全被循环B包含。

韦恩图：习题

示例 1

图 3表示一个韦恩图，显示了两个集合A和B，在一般情况下，我们对集合之间的任何关系一无所知。

注意，代表全集的矩形被划分为四个区域，分别标记为i、ii、iii和iv。

如果事实证明

（a）区域ii为空？

（b）区域iii为空？

（a）如果区域ii为空，则A不包含任何不属于B的元素。所以A是B的子集，并且应该像上面的图 2那样重新绘制图表。

（b）如果区域iii为空，则A和B没有共同的元素，因此是不相交的。然后应该像上面的图 1那样重新绘制图表。

示例 2

（a）绘制一个韦恩图来表示三个集合A、B和C，在一般情况下，我们对集合之间可能的关系一无所知。

（b）现在代表U的矩形被划分为多少个区域？

（c）当这些区域的各种组合为空时，讨论集合A、B和C之间的关系。

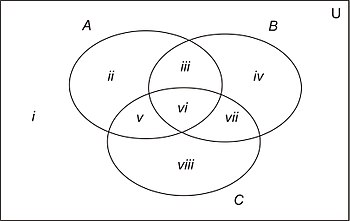
（a）图 4中的图表显示了三个集合的一般情况，我们对它们之间可能存在的任何关系一无所知。

（b）现在代表U的矩形被划分为 8 个区域，用罗马数字i到viii表示。

（c）各种组合的空区域都是可能的。在每种情况下，可以重新绘制韦恩图，以便不再包含空区域。例如

如果区域ii为空，则应缩小代表A的循环，并将其移动到B和C内部以消除区域ii。

如果区域ii、iii和iv为空，则缩小A和B，并将它们移动到C内部（从而消除所有这三个区域），但以一种它们仍然相互重叠的方式这样做（从而保留区域vi）。

如果区域iii和vi为空，则“拉开”循环A和B以消除这些区域，但保持每个循环与循环C重叠。

...等等。绘制上述每个示例的韦恩图留作读者练习。

示例 3

定义以下集合

U = {1, 2, 3, …, 10}

A = {2, 3, 7, 8, 9}

B = {2, 8}

C = {4, 6, 7, 10}

使用下面描述的两阶段技术，绘制一个文氏图来表示这些集合，并将所有元素标记在相应的区域中。

该技术如下

绘制一个“通用”的 3 集合文氏图，类似于示例 2中的那个。

一次只处理一个元素，遍历通用集合中的所有元素，并将每个元素输入到图表的相应区域。

如果需要，重新绘制图表，将循环移到彼此内部或彼此分开，以消除任何空区域。

不要先输入集合A的元素，然后输入集合B的元素，再输入集合C的元素，因为你可能会漏掉元素或者重复包含元素！

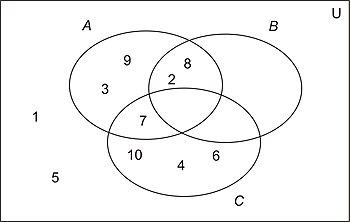
解决方案

在绘制了三个空循环后，绘制一个类似于图 4的图表（但没有罗马数字！），遍历U中的十个元素（数字 1 到 10），依次问每个元素三个问题，如下所示

第一个元素：1

你在A中吗？不

你在B中吗？不

你在C中吗？不

对所有三个问题的回答都是“否”，这意味着数字 1 在所有三个循环之外。因此，将其写入相应的区域（图 4中的区域编号i）。

第二个元素：2

你在A中吗？是

你在B中吗？是

你在C中吗？不

是，是，否：因此数字 2 在A和B内部，但在C外部。然后将其放入区域iii中。

… 等等，元素 3 到 10 也是如此。

生成的图表看起来像图 5。

最后一步是检查图表中是否有空区域 - 在本例中，我们称之为图 4中的iv、vi和vii的区域 - 然后重新绘制图表以消除这些区域。完成后，我们将清楚地看到三个集合之间的关系。

因此，我们需要

将B和C拉开，因为它们没有共同的元素。

将B推到A的内部，因为它在A外部没有元素。

最终结果显示在图 6中。

文氏图和真值表中的区域

也许你已经意识到，向文氏图添加一个额外的集合会将表示通用集合的矩形划分成的区域数量翻倍。这给了我们一个非常简单的模式，如下所示

用一个集合循环，将只有两个区域：循环内部和循环外部。

用两个集合循环，将有四个区域。

用三个循环，将有八个区域。

… 等等。

不难看出为什么应该是这样。我们向图表添加的每个新的循环都会将每个现有区域分成两个，从而使区域总数翻倍。

在A中吗？	在B中吗？	在C中吗？
Y	Y	Y
Y	Y	N
Y	N	Y
Y	N	N
N	Y	Y
N	Y	N
N	N	Y
N	N	N

但还有另一种看待这个问题的方式，那就是：在上面示例 3的解决方案中，我们对每个元素都问了三个问题：你在 A 中吗？你在 B 中吗？以及你在 C 中吗？现在，对每个问题显然都有两个可能的答案：是和否。当我们组合三个问题的答案时，一个接一个，那么总共有 2³ = 8 种可能的答案集。这八种可能的答案组合中的每一种都对应于文氏图上的不同区域。

完整的答案集与真值表非常相似 - 这是逻辑中的一个重要概念，逻辑处理可能为真或假的陈述。右边的表格显示了 3 个集合A、B和C的八种可能的答案组合。

你会发现研究每列中 Y 和 N 的模式很有帮助。

当你向下阅读C列时，字母在每一行都会改变：Y、N、Y、N、Y、N、Y、N

向下阅读B列，字母每隔一行就会改变：Y、Y、N、N、Y、Y、N、N

向下阅读A列，字母每隔四行就会改变：Y、Y、Y、Y、N、N、N、N

集合论练习 2

点击链接查看集合论练习 2

集合上的运算

正如我们可以将两个数字组合成第三个数字，使用像“加”、“减”、“乘”和“除”这样的运算，我们也可以用各种方式将两个集合组合成第三个集合。我们首先再看一下文氏图，它显示了两个集合A和B的通用位置，我们不知道它们之间有什么关系。

在A中吗？	在B中吗？	区域
Y	Y	iii
Y	N	ii
N	Y	iv
N	N	i

右边的表格中的前两列显示了对两个集合A和B提出问题你在 A 中吗？和你在 B 中吗？的四组可能的答案；第三列中的罗马数字显示了图 7中文氏图中的相应区域。

交集

区域iii，即两个循环重叠的地方（对应于“是”后跟“是”的区域），称为集合A和B的交集。它用A ∩ B表示。因此，我们可以将交集定义如下

两个集合A和B的交集，写作A ∩ B，是属于A并且属于B的元素的集合。

（请注意，在符号逻辑中，一个类似的符号， $\scriptstyle \wedge$ ，用于使用AND运算符连接两个逻辑命题。）

例如，如果A = {1、2、3、4} 且B = {2、4、6、8}，则A ∩ B = {2、4}。

因此，我们可以说，我们已经使用交集运算将两个集合组合成第三个集合。

并集

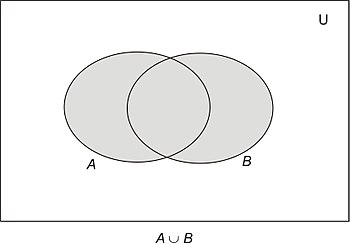
以类似的方式，我们可以将两个集合的并集定义如下

两个集合A和B的并集，写作A ∪ B，是属于A或属于B（或两者都属于）的元素的集合。

因此，并集由图 7中的区域ii、iii和iv表示。

（同样，在逻辑中，一个类似的符号， $\scriptstyle \vee$ ，用于使用OR运算符连接两个命题。）

因此，例如，{1、2、3、4} ∪ {2、4、6、8} = {1、2、3、4、6、8}。

你会看到，要进入交集，一个元素必须对两个问题都回答“是”，而要进入并集，任一答案都可以是“是”。

∪ 符号看起来像“Union”的第一个字母，也像一个可以容纳很多物品的杯子。∩ 符号看起来像一个溢出的杯子，不能容纳很多物品，或者可能像字母“n”，代表“i'n'tersection”。注意不要将两者混淆。

差集

两个集合A和B的差集（也称为A和B的集合论差集，或B在A中的相对补集）是属于A但不属于B的元素的集合。

这写成A - B，或者有时写成A \ B。

因此，差集中的元素是那些对第一个问题你在 A 中吗？回答“是”，但对第二个问题你在 B 中吗？回答“否”的元素。这种答案组合在上面表格的第 2 行，对应于图 7中的区域ii。

例如，如果A = {1、2、3、4} 且B = {2、4、6、8}，则A - B = {1、3}。

补集

到目前为止，我们已经考虑了两个集合组合成第三个集合的运算：二元运算。现在我们来看看一个一元运算——它只涉及一个集合。

集合 *A* 中**不包含**的元素的集合被称为 *A* 的**补集**。它被记作 *A*′（有时也记作 *A*^C 或 ${\bar {A}}$ ）。

显然，这是一个对问题“你在 *A* 中吗？”回答“否”的元素的集合。

例如，如果 **U** = **N** 且 *A* = {奇数}，则 *A*′ = {偶数}。

注意单词 *complement* 的拼写：它的字面意思是“互补的物品或项目”；换句话说，就是“完成某件事的东西”。因此，如果我们已经拥有了 *A* 的元素，那么 *A* 的补集就是 *完成* 整个全集的集合。

集合运算的性质

1. 交换律

$A\cup B=B\cup A$

$A\cap B=B\cap A$

2. 结合律

$A\cup (B\cup C)=(A\cup B)\cup C$

$A\cap (B\cap C)=(A\cap B)\cap C$

3. 分配律

$A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$

$A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

4. 补集的特殊性质

$(A')'=A$

$U'=\phi$

$\phi '=U$

$A\cap B'=A-B$

5. 德摩根定律

$(A\cap B)'=A'\cup B'$

$(A\cup B)'=A'\cap B'$ .

总结

交集：既在 A 中又在 B 中的东西	并集：在 A 中或在 B 中（或两者都在）的东西
差集：在 A 中但不在 B 中的东西	对称差：在 A 中或在 B 中，但不在两者中的东西
补集：不在 A 中的东西

基数

最后，在 *集合运算* 这一部分，我们看一下对集合进行操作，它得到的不是另一个集合，而是一个整数。

有限集合 *A* 的 *基数*，记作 | *A* |（有时记作 #( *A* ) 或 *n* ( *A* )），是 *A* 中的元素个数（不重复）。例如

如果A = {字母表的字母}, | A | = 26。

广义集合运算

如果我们想要表示n个集合的交集或并集，A₁, A₂, ..., A_n（我们可能不知道n的值）那么以下广义集合符号可能有用

A₁ ∩ A₂ ∩ ... ∩ A_n =

\scriptstyle \bigcap _{i=1}^{n}

A_i

A₁ ∪ A₂ ∪ ... ∪ A_n =

\scriptstyle \bigcup _{i=1}^{n}

A_i

在符号 $\scriptstyle \bigcap _{i=1}^{n}$ A_i中，i是一个变量，取值从1到n，表示所有集合A₁到A_n的重复交集。

集合论练习3

点击链接查看集合论练习3

离散数学
← 简介	集合论	集合论/第 2 页 →

交集：既在 A 中又在 B 中的东西	并集：在 A 中或在 B 中（或两者都在）的东西
差集：在 A 中但不在 B 中的东西	对称差：在 A 中或在 B 中，但不在两者中的东西
补集：不在 A 中的东西