离散数学/集合论/答案

集合论练习1答案

1

(a) 是；字母数字字符是A…Z、a…z和0…9

(b) 否；“高”没有明确定义

(c) 是；集合为{12.5}

(d) 是；空集

(e) 否；“好”没有明确定义

2

(a) T

(b) F

(c) T

(d) F；A是子集U（我们在下一节中会遇到）

(e) F；{偶数}是指所有偶数的集合，而不仅仅是2到10之间的偶数

3

(a) {4, 33, √9}

(b) {4, -5, 33, √9}

(c) {4, 2/3, -2.5, -5, 33, √9}

(d) {√2, π}

4

(a) F

(b) T

(c) F

(d) T

5个例子可能包括

(a) {伦敦，巴黎，罗马，…}

(b) {1, 3, 5, 7, …}，但不包括-3或-1

(c) {5, -5}

(d) {3, 27, 243, …}

返回 集合论练习1

集合论练习2答案

1

在A中？	在B中？	在C中？	区域
Y	Y	Y	vi
Y	Y	N	iii
Y	N	Y	v
Y	N	N	ii
N	Y	Y	vii
N	Y	N	iv
N	N	Y	viii
N	N	N	i

2

它们都相等。

3

(a) True (b) False (c) True

4

(a)

(b) P ⊂ Q; R ⊂Q

(c) False

5

(a)

(b)

(c)

(d)

返回 集合论练习2

集合论练习3答案

1

(a)	(b)
	A ∩ B = {6, 8} A ∪ C = {2, 3, 4, 6, 7, 8, 10} A ′ = {1, 3, 5, 7, 9} B ′ = {2, 4, 5, 9, 10} B ∩ A ′ = {1, 3, 7} B ∩ C ′ = {1, 6, 8} A – B = {2, 4, 10} A Δ B = {1, 2, 3, 4, 7, 10}

(c)

C - B =ø

2

(a) F

(b) F

(c) T

3

(a) P ⊆ Q

(b) Q ⊆ P

4

(a)	(b)
(c)	(d)
(e)	(f)

5

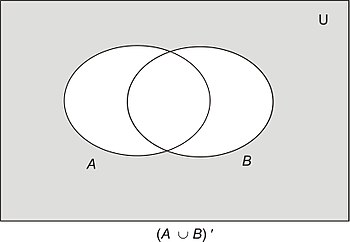
(a) B ′

(b) A ∩ B ′

(c) (A ∪ B) ∩ (A ∩ B) ′ or (A ∩ B ′) ∪ (A ′ ∩ B)

(d) (A ∩ B) ∪ (A ′ ∩ B ′) or (A ∪ B) ′ ∪ (A ∩ B) or …?

6

(a) 区域(b)代表A – B。所以A – B = A ∩ B ′

(b) 区域(c)代表A Δ B。

所以A Δ B = (A ∩ B) ∪ (A ′ ∩ B ′) or (A ∪ B) ′ ∪ (A ∩ B)

返回 集合论练习3

集合论练习4答案

1

(a) P(A) = {ø, {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {1, 4}, {2, 3}, {2,4}, {3, 4}, {2, 3, 4}, {1, 3, 4}, {1, 2, 4}, {1, 2, 3}, {1, 2, 3, 4}}

| P(A) | = 16

(b) 32

(c) 2¹⁰ = 1024

2

			使用定律
(a)	B ∪ (ø∩ A)	= B ∪ (A ∩ø)	交换律
		= B ∪ø	恒等律
		= B	恒等律
(b)	(A ' ∩ U) '	= (A' ) ' ∪ U'	德摩根定律
		= A ∪ U'	幂等律
		= A ∪ø	补律
		= A	恒等律
(c)	(C ∪ A) ∩ (B ∪ A)	= (A ∪ C) ∩ (B ∪ A)	交换律
		= (A ∪ C) ∩ (A ∪ B)	交换律
		= ((A ∪ C) ∩ B) ∪ ((A ∪ C) ∩ A)	分配律
		= ((A ∩ B) ∪ (C ∩ B)) ∪ (A ∪ (C ∩ A))	分配律
		= ((B ∩ C) ∪ (A ∩ B)) ∪ (A ∪ (A ∩ C))	交换律 (2x)
		= ((B ∩ C) ∪ (A ∩ B)) ∪ ((A ∩ U) ∪ (A ∩ C))	恒等律
		= ((B ∩ C) ∪ (A ∩ B)) ∪ (A ∩ (U ∪ C))	分配律
		= ((B ∩ C) ∪ (A ∩ B)) ∪ (A ∩ U)	恒等律
		= ((B ∩ C) ∪ (A ∩ B)) ∪ A	恒等律
		= (B ∩ C) ∪ ((A ∩ B) ∪ A))	结合律
		= (B ∩ C) ∪ ((A ∩ B) ∪ (A ∩ U))	恒等律
		= (B ∩ C) ∪ (A ∩ (B ∪ U))	分配律
		= (B ∩ C) ∪ (A ∩ U)	恒等律
		= (B ∩ C) ∪ A	恒等律
		= A ∪ (B ∩ C)	交换律
(d)	(A ∩ B) ∪ (A ∩ B ' )	= A ∩ (B ∪ B ' )	分配律
		= A ∩ U	补律
		= A	恒等律
(e)	(A ∩ B) ∪ (A ∪ B ' ) '	= (A ∩ B) ∪ (A ' ∩ (B ' ) ' )	德摩根定律
		= (A ∩ B) ∪ (A ' ∩ B)	幂等律
		= (B ∩ A) ∪ (B ∩ A ' )	交换律 (× 2)
		= B ∩ (A ∪ A ' )	分配律
		= B ∩ U	补律
		= B	恒等律
(f)	A ∩ (A ∪ B)	= (A ∪ø) ∩ (A ∪ B)	恒等律
		= A ∪ (ø∩ B)	分配律
		= A ∩ (B ∩ø)	交换律
		= A ∪ø	恒等律
		= A	恒等律

返回 集合论练习4

集合论练习5答案

1

(a) X × Y = {(a, a), (a, b), (a, e), (a, f), (c, a), (c, b), (c, e), (c, f)}

(b) Y × X = {(a, a), (a, c), (b, a), (b, c), (e, a), (e, c), (f, a), (f, c)}

(c) X × X = {(a, a), (a, c), (c, a), (c, c)}

(d) 它们相等：A = B

2

(a) (b, 2), (b, 4), (c, 1), (c, 5), (e, 1), (e, 5), (f, 2), (f, 4)

(b) P = C × R

(c) ((G × R) ∪ (C × T)) - (G × T)

3

V = {pqr | (p, q, r) ∈ L × (L ∪ D) × (L ∪ D)}

4

阴影区域在每种情况下都相同，因此命题似乎为真。

返回 集合论练习5