FHSST 物理/动量/性质

动量具有哪些性质？

在这一阶段，您可能想知道为什么要引入动量。值得注意的是，动量是一个守恒量。在孤立系统内，总动量是恒定的。无论孤立系统内的各个物体发生什么，系统的总动量都不会改变！由于动量是一个向量，它的守恒意味着它的幅度和方向都保持不变。

动量在孤立系统中守恒！

这个线性动量守恒定律是物理学中最基本的定律之一，它本身就证明了动量的定义是合理的。由于动量与物体的运动有关，我们可以利用它的守恒来预测碰撞和爆炸中发生的事情。如果我们将两个物体撞击在一起，根据动量守恒定律，碰撞前物体的总动量等于碰撞后物体的总动量。

线性动量守恒定律:

孤立系统的总线性动量是恒定的。

或者

在一个孤立系统中，碰撞前的总动量

(或爆炸) 等于碰撞后的总动量

(或爆炸)。

让我们考虑两个台球或撞球的简单碰撞。考虑第一个球 (质量 m₁) 的初始速度为 (${\overrightarrow {u_{1}}}$). 第二个球 (质量 m₂) 以初始速度 ${\overrightarrow {u_{2}}}$ 向第一个球运动。这种情况如图 6.1 所示。如果我们将每个球的动量加起来，我们就能得到系统的总动量。这个总动量为

${\begin{matrix}{\overrightarrow {p}}_{total\ before}=m_{1}{\overrightarrow {u_{1}}}+m_{2}{\overrightarrow {u_{2}}},\end{matrix}}$

文件:Fhsst mom2.png

图 6.1: 碰撞前。

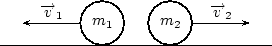
图 6.2: 碰撞后。

两个球碰撞后分离，它们各自具有不同的动量。如果我们将球 1 的最终速度称为 ${\overrightarrow {v_{1}}}$，球 2 的最终速度称为 ${\overrightarrow {v_{2}}}$ (见图 6.2)，那么碰撞后系统的总动量为

${\begin{matrix}{\overrightarrow {p}}_{total\ after}=m_{1}{\overrightarrow {v_{1}}}+m_{2}{\overrightarrow {v_{2}}},\end{matrix}}$

这个由两个球组成的系统是孤立的，因为没有外力作用在球上。因此，根据线性动量守恒定律，碰撞前的总动量等于碰撞后的总动量。这给出了两个物体碰撞中动量守恒的方程，

$m_{1}{\overrightarrow {u_{1}}}+m_{2}{\overrightarrow {u_{2}}}=m_{1}{\overrightarrow {v_{1}}}+m_{2}{\overrightarrow {v_{2}}}$
m1	: 物体 1 的质量 (kg)
m2	: 物体 2 的质量 (kg)
${\overrightarrow {u_{1}}}$	: 物体 1 的初始速度 (m.s-1 + 方向)
${\overrightarrow {u_{2}}}$	: 物体 2 的初速度 (m.s-1 + 方向)
${\overrightarrow {v_{1}}}$	: 物体 1 的末速度 (m.s-1 + 方向)
${\overrightarrow {v_{2}}}$	: 物体 2 的末速度 (m.s-1 + 方向)

该等式总是成立的 - 碰撞中动量守恒。

章节“碰撞与爆炸”涉及动量守恒的应用。