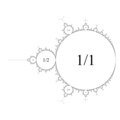
曼德勃罗集的拓扑模型

Thurston 模型（抽象的曼德勃罗集）^[1]
- Lavaurs 算法 ^[2]
- 抽象的曼德勃罗树 ^[3]
仙人掌模型 ^[4]（转到图像，其中包含算法的源代码和描述）
伪曼德勃罗集 = 没有毛发、细丝和原始双曲分量的 M 集^[5]

Lavaurs 算法

该算法展示了

如何计算落在曼德勃罗集根点的外部射线的角度
如何绘制图（圆上的层叠）显示曼德勃罗集的结构

落在曼德勃罗集周期 p 分量的根点的外部角（以转为单位，模 1）为

${\frac {n}{2^{p}-1}}$

弧线（弦）由以下部分组成：

落在相同根点的两个外部角
根点。

名称

二次次要层叠 = QML.
- 它是任何二次不变层叠的次要叶的集合。次要叶是层叠中最长叶的图像。^[6] 二次次要层叠的近似值仅包含周期性次要叶。
- 二次次要层叠 QML 包含树枝状二次多项式的次要标签。
与曼德勃罗集相关的圆上层叠
抽象的曼德勃罗集（Thurston）
曼德勃罗集的捏合圆盘模型：在捏合（粘合）圆上所有由弧线连接的点之后。它是与曼德勃罗集同胚的空间^[7]

数学描述

绘制单位圆 $S^{1}$
用单位圆中垂直于边界 $S^{1}$ 的弧线连接周期为二的角度：1/3 和 2/3
对于下一个周期，用弧线连接相同周期（第一和第二）的两个角度，使得
- 没有弧线交叉任何其他（先前的）弧线，
- 第一个角度是尚未连接的最小角度，第二个角度是尚未连接的下一个最小角度^[8]^[9]

周期 2
周期 3
周期 4
周期 5

程序员描述

在图像中间绘制以 (x0, y0) 为圆心、r0 为半径的主圆
选择周期，例如 p=3
计算角度对（以转为单位）
对于每个角度对 (alpha,beta)，使用新圆的一部分绘制一条弧线，该圆在 2 个点 c1、c2 处与主圆正交^[10]^[11]

计算角度对

（待办事项）

绘制连接角度的弧线

转换角度单位

第一个单位是转（角度对列表）

使用 ttr 函数

(defun ttr (turn)           
" Turns to Radians"
(* turn  (* 2 pi) ))

将它们转换为弧度

(alpha (ttr ( first angle-list)))

计算交点

主圆 (x0,y0,r0) 和新的正交圆 (x,y,r) 有 2 个公共点

c1 = (a,b) = (x0 + r0 * cos(alpha) , y0 + r0 * sin(alpha))
c2 = (x0 + r0 * cos(beta) , y0 + r0 * sin(beta))

(ca (cos alpha))
(sa (sin alpha))
; first common point 
(a (+ x0 (* r0 ca))) ; a = x0 + r0 * cos(alpha)
(b (+ y0 (* r0 sa))) ; b = y0 + r0 * sin(alpha)

计算正交圆

半径和圆心

在交点处，半径 r0 和新半径或正交圆也正交。新圆的圆心 (x,y) 位于通过点 (x0,y0) 且斜率由角度 gamma 定义的直线上。

gamma = alpha + (balpha - alpha)/2

(gamma (+ alpha (/ (- balpha alpha) 2))) ; angle between alpha and balpha

利用这些信息，可以计算新的圆：(x,y,r)

新角度

我们有

主圆 (x0, y0, r0)
新圆 (x, y, r)
交点 c1 和 c2 及其角度：alpha 和 beta

因为圆弧将使用新圆绘制，所以必须计算（转换）新角度（在新圆中测量的角度）。

点 c1 = (a,b) 在新圆单位中的角度。

 (phi  (atan r0 r))) ; phi = (new-alpha - new-balpha)
 (balha (+ pi gamma phi))  ; new balpha 
 (alpha (- (+ pi gamma) phi)) ; new alpha

绘制圆弧

这取决于可用的过程。

逐点绘制

最简单的情况是从点 c1 到 c2 绘制圆弧。

Postscript

在 Postscript 中，有 arct 过程：^[12]

x1 y1 x2 y2 r arct

因此，在 Lisp 中，可以直接创建 ps 文件并使用此过程。

; code by Copyright 2009 Rubén Berenguel
; http://www.mostlymaths.net/2009/08/lavaurs-algorithm.html
(defun DrawArc (alpha balpha R)
  "Generate the postscript arcs using arct 
   x1 y1 x2 y2 r arct "
  (format t "newpath ~A ~A moveto 300 300 ~A ~A ~A arct" 
	  (+ 300 (* 100 (cos balpha))) 
	  (+ 300 (* 100 (sin balpha)))
	  (+ 300 (* 100 (cos alpha))) 
	  (+ 300 (* 100 (sin alpha)))
	  R))

SVG

在 SVG 中，有椭圆弧曲线命令。^[13]^[14]^[15]^[16]^[17]^[18]

它是路径命令的一个版本，用于从当前点到 (x, y) 绘制椭圆弧。

椭圆的大小和方向由两个半径 (rx, ry) 和一个 x 轴旋转定义，它指示椭圆整体相对于当前坐标系的旋转方式。

椭圆的中心 (cx, cy) 是自动计算的，以满足其他参数施加的约束。

large-arc-flag 和 sweep-flag 有助于自动计算并帮助确定如何绘制圆弧。

rx ry x-axis-rotation large-arc-flag sweep-flag x y

<path d="M 100,100 a100,100 0 0,0 100,50" fill="none" stroke="red" stroke-width="6" />

<?xml version="1.0" standalone="no"?>
<svg width="800px" height="800px" version="1.1" xmlns="http://www.w3.org/2000/svg">
  <path d="M100 100
           A 100 100 0 0 0 162.55 162.45
           " stroke="black" fill="none" stroke-width="2" fill-opacity="0.5"/>
</svg>

SVG 路径元素

M100 100 指定圆弧的绝对起点 (100,100)
A 100 100 表示此圆弧的长轴和短轴长度相同 = 100
0 0 0 分别是 x 轴旋转、large-arc-flag 和 sweep-flag
162.55 162.45 是圆弧的终点

因此，可以通过像这样向 svg 文件写入路径命令来绘制圆弧。

(format stream-name "<path d=\"M~,0f ~,0f A~,0f ~,0f 0 0 0 ~,0f ~,0f\"  />~%" 
	(first arc-list)
	(second arc-list)
	(third arc-list)
	(third arc-list)
	(fourth arc-list)  ; 
 	(fifth arc-list))

请记住，SVG 中的**初始坐标系**原点位于左上角，x 轴指向右侧，y 轴指向下方。^[19]对于绘制所有圆弧，这可能并不重要，但带有角度的标签将不正确。

角到角绘制

这种情况比较困难，因为必须将角度从主圆转换为新的正交圆。当角度转换后，

将当前点移动到圆弧的第一个点（交点）。此处 c1 = (a,b)
绘制圆弧。顺时针绘制圆弧比逆时针绘制更容易。

在 Vecto Common Lisp 包中，有 arcn 过程 ^[20]

(vecto:move-to ( sixth arc-list) (seventh arc-list)) ; beginning of arc is point (a,b)
(vecto:arcn
	( first arc-list)  ; x
	(second arc-list)  ; y
	(third arc-list)   ; radius
	(fourth arc-list)  ; angle1
 	(fifth arc-list))) ; angle2

 (vecto:stroke)

代码示例

Common Lisp 代码
- 用于由 Ruben Berenguel 绘制 poscript 文件^[21]
- 用于使用 Vecto 包绘制 png 文件
- 用于绘制 svg 文件
Claude Heiland-Allen 编写的带有 SVG 输出的 Haskell 代码
来自程序 Mandel by Wolf Jung 第 4 页第 7 页的 c++ 代码

参考文献

↑ 曼德勃罗集中的组合学 - Lavaurs 算法
↑ Lavaurs 算法用 Lisp 实现 by Ruben Berenguel
↑ 抽象曼德勃罗树
↑ 曼德勃罗仙人掌
↑ Burns A M : : 绘制逃逸 - 曼德勃罗集中抛物线分叉的动画。数学杂志：第 75 卷，第 2 期，第 104-116 页，第 104 页
↑ Freddie Exall : 等价交配简介
↑ A. DOUADY，计算曼德勃罗集中角度的算法（混沌动力学和分形，由 Barnsley 和 Demko 编辑，Acad. Press，1986 年，第 155-168 页）。
↑ Lavaurs，P.，“M 在奇数分母有理数上定义的内卷的组合描述”，C. R. Acad. Sci. Paris 303（1986），143-146。
↑ 曼德勃罗集中的组合学 - Lavaurs 算法
↑ 从耶鲁大学的分形几何构建正交圆
↑ planetmath.org 上的正交圆
↑ Postscript 运算符
↑ SVG 文档：椭圆弧曲线命令
↑ svg 基础圆弧描述
↑ 椭圆弧实现说明
↑ Mozilla 开发者中心路径
↑ Pilat Informative Educative 圆弧
↑ O'Reilly 文档
↑ 初始坐标系 - w3.org 上的 SVG 文档
↑ Zach Beane 编写的 Vecto Common Lisp 包中的 arcn 过程。
↑ Ruben Berenguel 的 Lavaurs 算法

另请参阅

层叠
Julia 集的层叠
圆的无交叉划分

Mandelbrot 集的拓扑模型（反映对象的结构）。没有迷你 Mandelbrot 集和 Misiurewicz 点的 Mandelbrot 集的拓扑模型（仙人掌模型）
分形旋转裁剪
Mandelbrot 集的灌木模型

[1] 曼德勃罗集中的组合学 - Lavaurs 算法

[2] Lavaurs 算法用 Lisp 实现 by Ruben Berenguel

[3] 抽象曼德勃罗树

[4] 曼德勃罗仙人掌

[5] Burns A M : : 绘制逃逸 - 曼德勃罗集中抛物线分叉的动画。数学杂志：第 75 卷，第 2 期，第 104-116 页，第 104 页

[6] Freddie Exall : 等价交配简介

[7] A. DOUADY，计算曼德勃罗集中角度的算法（混沌动力学和分形，由 Barnsley 和 Demko 编辑，Acad. Press，1986 年，第 155-168 页）。

[8] Lavaurs，P.，“M 在奇数分母有理数上定义的内卷的组合描述”，C. R. Acad. Sci. Paris 303（1986），143-146。

[9] 曼德勃罗集中的组合学 - Lavaurs 算法

[10] 从耶鲁大学的分形几何构建正交圆

[11] tmath.org 上的正交圆

[12] Postscript 运算符

[13] SVG 文档：椭圆弧曲线命令

[14] svg 基础圆弧描述

[15] 椭圆弧实现说明

[16] Mozilla 开发者中心路径

[17] Pilat Informative Educative 圆弧

[18] O'Reilly 文档

[19] 初始坐标系 - w3.org 上的 SVG 文档

[20] Zach Beane 编写的 Vecto Common Lisp 包中的 arcn 过程。

[21] Ruben Berenguel 的 Lavaurs 算法

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]