|
此模块可能需要完全重写以适合其目标受众。
你可以帮助重写它。请查看相关讨论。 |
在本节中,我们将展示如何从三个线段构造一个三角形。构造基于第一卷,命题22
给定三个线段 ,
, 和
和 ,我们构建一个边长等于这些线段的三角形。
,我们构建一个边长等于这些线段的三角形。
- 复制直线
 到点A。
到点A。
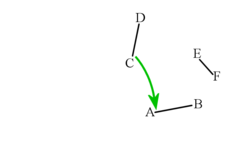
如果你忘记了如何操作,请遵循上一节的说明。你的构造应该看起来像下图中的灰色线。将新线称为

现在最好擦除你的辅助线,这样就只剩下下面显示的四条线段。

- 复制直线
 到点B。
到点B。
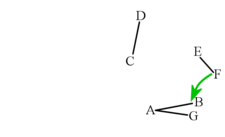
你的构造应该看起来像下图中的灰色线。将新线称为

- 画圆
 ,其圆心为A,半径为
,其圆心为A,半径为 。
。
- 画圆
 ,其圆心为B,半径为
,其圆心为B,半径为 。
。
- 设J为
 和
和 的交点。
的交点。

- 画一条线
 .
.
- 画一条线
 .
.
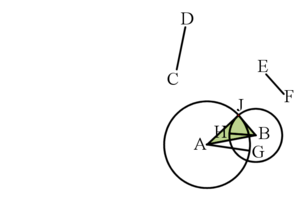
三角形  的边分别等于
的边分别等于  ,
,  和
和  .
.
- 线段
 是三角形的边,等于它本身。
是三角形的边,等于它本身。
- 线段
 等于
等于  ,因为它们都是圆
,因为它们都是圆 的半径。并且因为它是复制的,所以
的半径。并且因为它是复制的,所以 =
= 。因此
。因此  也等于
也等于 
- 线段
 等于
等于  ,因为它们都是圆
,因为它们都是圆  的半径。并且由于它是复制的,
的半径。并且由于它是复制的, =
= 。因此,
。因此, 也等于
也等于 
- 因此,三角形
 的边分别等于
的边分别等于  、
、 和
和  。
。
- 画一条线
 ,长度随意。
,长度随意。
- 复制这条线
 到任意点 C,得到
到任意点 C,得到  。
。
- 画一条线
 ,使其长度为
,使其长度为  长度的三倍。(我们没有指定如何构建这样的线段,留作练习。参考章节 复制线段 来解决。)
长度的三倍。(我们没有指定如何构建这样的线段,留作练习。参考章节 复制线段 来解决。)
- 用
 、
、 和
和  构造一个三角形。
构造一个三角形。
我们在测试中无法构建三角形的原因是,我们构造的圆圈没有相交。不能用任意三条线段来构造三角形。线段的长度必须满足一个称为“三角形不等式”的条件。三角形不等式指出,任何一条线段都应小于另外两条线段长度的总和。如果其中一条线段更长,则圆圈就不会相交。如果一条线段等于另外两条线段的总和,我们会得到一条直线而不是三角形。
因此,构造是正确的,但应该对可以应用构造的线段进行条件限制。请注意,原始构造是欧几里得提出的,因此构造或其证明中不存在错误。
























