游戏开发指南/理论/数学/向量

3D 向量的示例

符号

向量用于存储变量的多个分量，通常是空间维度的轴。因此，它们通常用于 2D 或 3D。

实际上，有两种方法可以表示向量

2D

这可以定义为“旋转和大小”或“x 方向上的位移和 y 方向上的位移”。

3D

这可以定义为“xz 方向上的旋转、y 方向上的旋转和大小”或“x 方向上的位移、y 方向上的位移和 z 方向上的位移”。

通常，在游戏中，我们使用维度上的位移版本，而不是大小和旋转。

向量可以有多种形式

i、j、k 形式 - 其中 i 表示 x 轴 上的 1 个单位，j 表示 y 轴 上的 1 个单位，如果是在 3D 中，k 表示 z 轴 上的 1 个单位

在 2D 中，它看起来像这样：$3i+4j$，其中 3 表示 正 x 轴 上的 3 个单位，4 表示 正 y 轴 上的 4 个单位。

在 3D 中，它看起来像这样：$6i-3j+5k$，其中 6 表示 正 x 轴 上的 6 个单位，-3 表示 负 y 轴 上的 3 个单位，5 表示 正 z 轴 上的 5 个单位。

列向量 - 这是最常见的向量形式。

在 2D 中，它看起来像这样：${\begin{pmatrix}3\\4\end{pmatrix}}$，其中 3 表示 正 x 轴 上的 3 个单位，4 表示 正 y 轴 上的 4 个单位。

在 3D 中，它看起来像这样：${\begin{pmatrix}6\\-3\\5\end{pmatrix}}$，其中 6 表示 正 x 轴 上的 6 个单位，-3 表示 负 y 轴 上的 3 个单位，5 表示 正 z 轴 上的 5 个单位。

行向量 - 这是最不常见的向量形式。

在 2D 中，它看起来像这样：${\begin{pmatrix}3&4\end{pmatrix}}$，其中 3 表示 正 x 轴 上的 3 个单位，4 表示 正 y 轴 上的 4 个单位。

在 3D 中，它看起来像这样：${\begin{pmatrix}6&-3&5\end{pmatrix}}$，其中 6 表示 正 x 轴 上的 6 个单位，-3 表示 负 y 轴 上的 3 个单位，5 表示 正 z 轴 上的 5 个单位。

在写向量时，你可以用这种方式表示它

${\overrightarrow {V}}$ 或只是 ${\textbf {V}}$

从一个位置到另一个位置（从 A 到 B）时，可以这样写

${\overrightarrow {AB}}$

向量加减法

加向量就像加同类项一样简单。

加法

${\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}+{\begin{pmatrix}x_{2}\\y_{2}\\z_{2}\end{pmatrix}}={\begin{pmatrix}x_{1}+x_{2}\\y_{1}+y_{2}\\z_{1}+z_{2}\end{pmatrix}}$

减法

${\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}-{\begin{pmatrix}x_{2}\\y_{2}\\z_{2}\end{pmatrix}}={\begin{pmatrix}x_{1}-x_{2}\\y_{1}-y_{2}\\z_{1}-z_{2}\end{pmatrix}}$

注意：将常数加减到向量中是未定义的。

向量与常数的乘除（标量倍数）

当一个常数乘以/除以一个向量时，你只需将该乘以/除以操作应用于向量的所有分量。

乘法

$c{\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}={\begin{pmatrix}cx_{1}\\cy_{1}\\cz_{1}\end{pmatrix}}$

除法

${\frac {\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}{c}}={\frac {1}{c}}{\begin{pmatrix}x_{1}\\y_{1}\\z_{1}\end{pmatrix}}={\begin{pmatrix}{\frac {x_{1}}{c}}\\{\frac {y_{1}}{c}}\\{\frac {z_{1}}{c}}\end{pmatrix}}$

当一个向量乘以另一个向量时，有两种定义的向量乘法方式：向量点积 和 向量叉积。

单位长度向量

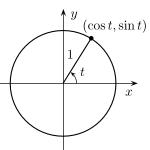二维中的单位向量基于此，这意味着x和y不能同时为1，否则它将不会形成一个圆，而是形成一个正方形，并且大小将大于1（一个单位）。

当大小不重要，只有方向重要时，使用单位向量。在二维中，它基于单位圆，在三维中，它基于单位球；x、y和z的值介于-1和1之间。

它的表示法是：${\hat {\textbf {V}}}$

要将向量转换为单位长度向量，请使用以下公式：${\hat {\textbf {V}}}={\frac {\overrightarrow {\textbf {V}}}{{\Big |}{\overrightarrow {\textbf {V}}}{\Big |}}}$，这被称为归一化向量。

零向量

零向量（有时称为零向量）是一个所有内容都是 0 的向量。如果零向量用 ${\overrightarrow {V}}$ 表示；

... 并且它在 2D 中，它看起来像：${\overrightarrow {V}}={\begin{pmatrix}0\\0\end{pmatrix}}$

... 并且它在 3D 中，它看起来像：${\overrightarrow {V}}={\begin{pmatrix}0\\0\\0\end{pmatrix}}$

... 并且它在 $N$D 中，它看起来像：${\overrightarrow {V}}={\begin{pmatrix}0\\0\\\vdots \\0\end{pmatrix}}$

零位置向量的示例是原点；这是因为它有一个原点 $(0,0)$ 或 $(0,0,0)$。

另一个示例是，如果您想停止物体移动，您可以将 速度 设置为零向量。

大小

由于向量由许多部分组成，因此用于每个维度的数字表示每个方向的距离。为了找到对角线穿过维度的点到点的距离，您需要找到向量的模。

二维向量的模由（根据勾股定理）给出

$|{\overrightarrow {V}}|={\sqrt {V_{x}^{2}+V_{y}^{2}}}$

三维向量的模由给出

$|{\overrightarrow {V}}|={\sqrt {V_{x}^{2}+V_{y}^{2}+V_{z}^{2}}}$

位置向量

位置向量是一个被视为坐标的向量，因此它是一个从原点到点的向量。字母O 通常用于表示原点。

位置向量可以写成

${\overrightarrow {OA}}$

${\overrightarrow {OA}}={\begin{pmatrix}1\\0\\-3\end{pmatrix}}$ 等同于说有一个点 $A$，其坐标为：$(1,0,-3)$

计算两个位置向量之间的向量

${\overrightarrow {ba}}={\overrightarrow {a}}-{\overrightarrow {b}}$

${\overrightarrow {AB}}={\overrightarrow {OB}}-{\overrightarrow {OA}}$

${\overrightarrow {BA}}={\overrightarrow {OA}}-{\overrightarrow {OB}}$

练习：找出这些位置向量之间的向量 已知 ${\overrightarrow {OA}}={\begin{pmatrix}1\\0\\-3\end{pmatrix}}$ 和 ${\overrightarrow {OB}}={\begin{pmatrix}3\\2\\7\end{pmatrix}}$，求 ${\overrightarrow {AB}}$ 答案 ${\overrightarrow {AB}}={\begin{pmatrix}3\\2\\7\end{pmatrix}}-{\begin{pmatrix}1\\0\\-3\end{pmatrix}}$ ${\overrightarrow {AB}}={\begin{pmatrix}2\\2\\10\end{pmatrix}}$

点积

点积有两个公式

${\overrightarrow {A}}\cdot {\overrightarrow {B}}=|{\overrightarrow {A}}||{\overrightarrow {B}}|\cos(\theta )$ 其中 $\theta$ 是两个向量之间的夹角。

${\overrightarrow {A}}\cdot {\overrightarrow {B}}={\overrightarrow {A_{x}}}{\overrightarrow {B_{x}}}+{\overrightarrow {A_{y}}}{\overrightarrow {B_{y}}}+{\overrightarrow {A_{z}}}{\overrightarrow {B_{z}}}$

两个向量的夹角

从这些公式，我们可以得到另一个计算它们之间夹角的公式

$\theta =\cos ^{-1}{\Bigg (}{\frac {{\overrightarrow {A}}\cdot {\overrightarrow {B}}}{|{\overrightarrow {A}}||{\overrightarrow {B}}|}}{\Bigg )}=\cos ^{-1}{\Bigg (}{\frac {{\overrightarrow {A_{x}}}{\overrightarrow {B_{x}}}+{\overrightarrow {A_{y}}}{\overrightarrow {B_{y}}}+{\overrightarrow {A_{z}}}{\overrightarrow {B_{z}}}}{|{\overrightarrow {A}}||{\overrightarrow {B}}|}}{\Bigg )}$

如果 ${\overrightarrow {A}}\cdot {\overrightarrow {B}}=0$，则这意味着这两个向量是垂直的。

要注意的是 ${\overrightarrow {A}}\cdot {\overrightarrow {B}}={\overrightarrow {B}}\cdot {\overrightarrow {A}}$。

标量投影

标量投影

标量投影（或标量分量）是求一个向量（**A**）在另一个向量（**B**）上的投影的长度。

${\bigg |}proj_{\overrightarrow {B}}{\overrightarrow {A}}{\bigg |}=|{\overrightarrow {A}}|\cos \theta ={\frac {{\overrightarrow {A}}\cdot {\overrightarrow {B}}}{|{\overrightarrow {B}}|}}$

其中θ是**A**和**B**之间的夹角。

这个投影的向量（**A** 投影到 **B** 上）也可以用下面的公式求出

$proj_{\overrightarrow {B}}{\overrightarrow {A}}={\frac {{\overrightarrow {A}}\cdot {\overrightarrow {B}}}{|{\overrightarrow {B}}|^{2}}}{\overrightarrow {B}}$

向量方程

一个基本的向量方程由一个向量和另一个向量的变量系数组成。独立的向量被称为位置向量，而带有变量系数的向量被称为方向向量。位置向量表示向量在3D空间中的位置，而方向向量表示向量指向的方向。位置向量的向量可以是直线上任何点的的位矢。

一个典型的方程可能看起来像这样: ${\textbf {r}}={\textbf {a}}+x{\textbf {b}}$ 或者 ${\textbf {r}}={\begin{pmatrix}2\\2\\2\end{pmatrix}}+x{\begin{pmatrix}1\\-2\\3\end{pmatrix}}$

检查直线是否平行

当直线的方向向量是彼此的标量倍数时，这些直线是平行的。

示例

直线 1: ${\textbf {r}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+\lambda {\begin{pmatrix}1\\-2\\3\end{pmatrix}}$ 直线 2: ${\textbf {s}}={\begin{pmatrix}2\\5\\7\end{pmatrix}}+\mu {\begin{pmatrix}-2\\4\\-6\end{pmatrix}}$

它们是平行的，因为 $-2{\begin{pmatrix}1\\-2\\3\end{pmatrix}}={\begin{pmatrix}-2\\4\\-6\end{pmatrix}}$.

检查一个点是否位于向量直线方程上

所以，如果该点的位置向量是 ${\textbf {P}}={\begin{pmatrix}2\\4\\4\end{pmatrix}}$，而直线方程是 ${\textbf {r}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\3\end{pmatrix}}$，并且你想看看 **P** 是否位于 **直线** 上，那么你需要执行以下操作

将 **点** 等于 **方程**

${\begin{pmatrix}2\\4\\4\end{pmatrix}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\3\end{pmatrix}}$

从此你可以从每行创建 3 个独立的方程

$2=1+2t$

$4=2+4t$

$4=3+3t$

然后解出每个方程以找到 **t**

$2=1+2t$ → $t={\frac {1}{2}}$

$4=2+4t$ → $t={\frac {1}{2}}$

$4=3+3t$ → $t={\frac {1}{3}}$

只有当所有 3 个 **t** 的值都相同时，**点** 才在 **直线** 上，因为其中一个 **t** 值与另外两个不同，所以 **点** 不在 **直线** 上。

检查两个向量直线方程是否相交

因此，在这个例子中，你需要两条直线，直线 1：${\textbf {r}}={\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\2\end{pmatrix}}$ 和直线 2：${\textbf {s}}={\begin{pmatrix}4\\4\\2\end{pmatrix}}+u{\begin{pmatrix}1\\-2\\-3\end{pmatrix}}$

然后你需要将这两个方程设为相等。

${\begin{pmatrix}1\\2\\3\end{pmatrix}}+t{\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}4\\4\\2\end{pmatrix}}+u{\begin{pmatrix}1\\-2\\-3\end{pmatrix}}$

然后减去一组常数以将常数保留在一侧。

$t{\begin{pmatrix}2\\4\\2\end{pmatrix}}={\begin{pmatrix}3\\2\\-1\end{pmatrix}}+u{\begin{pmatrix}1\\-2\\-3\end{pmatrix}}$

由此，你可以从每一行创建一个方程

$2t=3+u$

$4t=2-2u$

$2t=-1-3u$

在找到 t 和 u 的值时，你只需要使用两个方程，这样你就可以检查第三个方程是否匹配（在 2D 中不需要此检查步骤）。我将使用方程 1 和方程 2： *使用任何你想要的联立方程求解方法*

$2t=3+u$ → $4t=6+2u$ *将此方程的两边都乘以 2*

$4t=2-2u$

$0=4+4u$ *得到方程 1，并从中减去方程 2*

$u=-1$ 求解得到u

$4t=6+2(-1)$ 将u代回方程1

$t=1$ 求解得到t

现在让我们检查一下它是否适用于最终方程式，将u和t的值代入你没有用过的方程式。

$2t=-1-3u$

$2(1)=-1-3(-1)$

$2=2$

如果你得到一个等式表达式（一个常数等于它自身），这意味着它们相交，否则它们不相交。这被称为斜交。

直线方程上距离另一个点最近的点以及它们之间的距离

假设有一个向量方程${\textbf {r}}={\begin{pmatrix}2\\2\\2\end{pmatrix}}+t{\begin{pmatrix}1\\-2\\3\end{pmatrix}}$，并且有一个点P，其位置向量为：${\overrightarrow {OP}}={\begin{pmatrix}1\\1\\2\end{pmatrix}}$。我们想要找到直线上距离P最近的点的坐标以及该点和P之间的距离。

我们将直线上的这个点称为X。

首先，我们需要使用我们的点积规则，因为从P到X的直线将垂直于直线本身。为此，我们需要找到直线的方向和从P到X的向量。

直线的方向就是直线的方向向量（我们称之为A）：${\textbf {A}}={\begin{pmatrix}1\\-2\\3\end{pmatrix}}$

至于P到X的方向，我们需要先找到X，即使它用t表示。

X就是直线方程本身写成一个向量

${\overrightarrow {OX}}={\begin{pmatrix}2+t\\2-2t\\2+3t\end{pmatrix}}$

由此，我们可以使用“计算两个位置向量之间的向量”找到用t表示的${\overrightarrow {PX}}$：

${\overrightarrow {PX}}={\overrightarrow {OX}}-{\overrightarrow {OP}}={\begin{pmatrix}2+t\\2-2t\\2+3t\end{pmatrix}}-{\begin{pmatrix}1\\1\\2\end{pmatrix}}={\begin{pmatrix}1+t\\1-2t\\3t\end{pmatrix}}$

现在我们有了两个方向，就可以使用点积了

${\textbf {A}}\cdot {\overrightarrow {PX}}=0$

${\textbf {A}}_{x}{\overrightarrow {PX}}_{x}+{\textbf {A}}_{y}{\overrightarrow {PX}}_{y}+{\textbf {A}}_{z}{\overrightarrow {PX}}_{z}=0$

$1(1+t)-2(1-2t)+3(3t)=0$

$(1+t)(4t-2)+(9t)=0$

$14t-1=0$

$t={\frac {1}{14}}$

现在我们有了t的值，可以将其代入${\overrightarrow {OX}}$的方程式中

${\overrightarrow {OX}}={\begin{pmatrix}2+t\\2-2t\\2+3t\end{pmatrix}}={\begin{pmatrix}2+{\frac {1}{14}}\\2-2({\frac {1}{14}})\\2+3({\frac {1}{14}})\end{pmatrix}}={\begin{pmatrix}{\frac {29}{14}}\\{\frac {13}{7}}\\{\frac {31}{14}}\end{pmatrix}}$，这就是我们一直在寻找的位置向量（X）。

至于P和X之间的距离，我们需要将t代入我们的${\overrightarrow {PX}}$方程式中

${\overrightarrow {PX}}={\begin{pmatrix}1+t\\1-2t\\3t\end{pmatrix}}={\begin{pmatrix}1+{\frac {1}{14}}\\1-2({\frac {1}{14}})\\3({\frac {1}{14}})\end{pmatrix}}={\begin{pmatrix}{\frac {15}{14}}\\{\frac {6}{7}}\\{\frac {3}{14}}\end{pmatrix}}$

这是我们的向量，现在我们只需要找到向量的长度/大小

$|{\overrightarrow {PX}}|={\sqrt {{\overrightarrow {PX}}_{x}^{2}+{\overrightarrow {PX}}_{y}^{2}+{\overrightarrow {PX}}_{z}^{2}}}={\sqrt {{\bigg (}{\frac {15}{14}}{\bigg )}^{2}+{\bigg (}{\frac {6}{7}}{\bigg )}^{2}+{\bigg (}{\frac {3}{14}}{\bigg )}^{2}}}={\sqrt {{\frac {225}{196}}+{\frac {36}{49}}+{\frac {9}{196}}}}={\sqrt {\frac {27}{14}}}={\frac {3{\sqrt {42}}}{14}}$ ≈ $1.38873$, 这是 **点 P 到直线上最近点 X 的距离**。

叉积

叉积 (左), 右手定则 (右)

叉积定义为： ${\overrightarrow {A}}\times {\overrightarrow {B}}=|{\overrightarrow {A}}||{\overrightarrow {B}}|\sin(\theta ){\hat {n}}$，其中 $\theta$ 是 它们之间的夹角，而 ${\hat {n}}$ 是一个 单位向量，它同时垂直于 ${\overrightarrow {A}}$ 和 ${\overrightarrow {B}}$。叉积只在 3 维和 7 维中有效 (你不需要 7 维版本)。

有两个向量同时垂直于 A 和 B，一个指向页面/屏幕外，另一个指向屏幕内。一个是 ${\overrightarrow {A}}\times {\overrightarrow {B}}$，另一个是 ${\overrightarrow {B}}\times {\overrightarrow {A}}$。由于它们都指向不同的方向，并且大小相同，这意味着：${\overrightarrow {A}}\times {\overrightarrow {B}}=-{\overrightarrow {B}}\times {\overrightarrow {A}}$。你可以使用 右手定则 来找到叉积向量的方向。

由于你的电脑没有 "右手"，你可以使用这个公式，它能做同样的事情

${\overrightarrow {A}}\times {\overrightarrow {B}}={\overrightarrow {C}}={\begin{pmatrix}A_{y}B_{z}-A_{z}B_{y}\\A_{z}B_{x}-A_{x}B_{z}\\A_{x}B_{y}-A_{y}B_{x}\end{pmatrix}}$

法向量

法向量是一个指向几何体表面向外的单位长度向量。对于每块平面几何体，存在两个法向量，一个直接向上（相对于表面），另一个直接向下（相对于表面），使得一个与另一个相反。

计算法向量

要计算法向量，首先需要找到几何体的一个角点。在该点处将有两个边延伸出来。你需要找到这两条边的向量。然后你需要找到边 1 (E₁) 和边 2 (E₂) 的叉积。之后你需要将向量归一化使其单位长度。

${\overrightarrow {E_{1}}}\times {\overrightarrow {E_{2}}}={\overrightarrow {n_{1}}}$

${\hat {n_{1}}}={\frac {\overrightarrow {n_{1}}}{|{\overrightarrow {n_{1}}}|}}$

重写成一个方程

${\hat {n_{1}}}={\frac {{\overrightarrow {E_{1}}}\times {\overrightarrow {E_{2}}}}{|{\overrightarrow {E_{1}}}\times {\overrightarrow {E_{2}}}|}}$

注意：从数学上来说，这更好，但在计算上更差，使用计算机时使用第一个版本来避免计算两次叉积。这将需要存储一个额外的变量，但对于处理器来说要容易得多。

要找到另一个法向量 (n₂)，可以使用以下任一方程

${\hat {n_{2}}}={\frac {{\overrightarrow {E_{2}}}\times {\overrightarrow {E_{1}}}}{|{\overrightarrow {E_{2}}}\times {\overrightarrow {E_{1}}}|}}$ 或者 ${\hat {n_{2}}}=-{\hat {n_{1}}}$

参见

• 在代码中创建 vector3 类

外部链接

• Khan Academy 关于叉积的视频，解释右手定则：第一集 第二集
• Jorge Rodriguez 关于叉积的视频，包含计算机版本：https://www.youtube.com/watch?v=FT7MShdqK6w