线性代数/Gram-Schmidt 正交化

本小节为可选内容。它需要前一个小节的内容，前一个小节也是可选内容。这里完成的工作只在第五章的最后两个部分需要。

前一个小节表明，投影到由 ${\vec {s}}$ 张成的直线上将向量 ${\vec {v}}$ 分解成两个部分

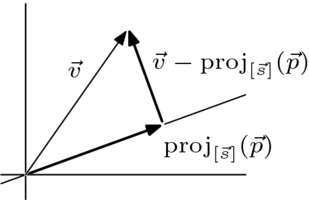
$\displaystyle {\vec {v}}={\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})\,+\,\left({\vec {v}}-{\mbox{proj}}_{[{\vec {s}}\,]}({\vec {v}})\right)$

它们是正交的，所以是“不交互的”。我们现在将发展这个建议。

定义 2.1

向量 ${\vec {v}}_{1},\dots ,{\vec {v}}_{k}\in \mathbb {R} ^{n}$ 当任何两个向量正交时是 **相互正交** 的：如果 $i\neq j$ 那么点积 ${\vec {v}}_{i}\cdot {\vec {v}}_{j}$ 为零。

定理 2.2

如果集合 $\{{\vec {v}}_{1},\dots ,{\vec {v}}_{k}\}\subset \mathbb {R} ^{n}$ 中的向量是相互正交且非零的，那么这个集合是线性无关的。

证明

考虑线性关系 $c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}+\dots +c_{k}{\vec {v}}_{k}={\vec {0}}$。 如果 $i\in [1..k]$，那么对等式两边与 ${\vec {v}}_{i}$ 进行点积

${\begin{array}{rl}{\vec {v}}_{i}\cdot (c_{1}{\vec {v}}_{1}+c_{2}{\vec {v}}_{2}+\dots +c_{k}{\vec {v}}_{k})&={\vec {v}}_{i}\cdot {\vec {0}}\\c_{i}\cdot ({\vec {v}}_{i}\cdot {\vec {v}}_{i})&=0\end{array}}$

表明，因为 ${\vec {v}}_{i}$ 不为零，则 $c_{i}$ 为零。

推论 2.3

如果一个 $k$ 维空间中的大小为 $k$ 的向量子集是相互正交且非零的，那么该集合是该空间的基底。

证明

任何线性无关的大小为 $k$ 的 $k$ 维空间的子集是一个基底。

当然，推论 2.3 的逆命题不成立——并非所有 $\mathbb {R} ^{n}$ 的子空间的基底都由相互正交的向量组成。然而，我们可以得到一个部分逆命题，即对于 $\mathbb {R} ^{n}$ 的每一个子空间，至少存在一个由相互正交的向量组成的基底。

示例 2.4

该基底 $\mathbb {R} ^{2}$ 的成员 ${\vec {\beta }}_{1}$ 和 ${\vec {\beta }}_{2}$ 不是正交的。

$\displaystyle B=\left\langle {\begin{pmatrix}4\\2\end{pmatrix}},{\begin{pmatrix}1\\3\end{pmatrix}}\right\rangle$

然而，我们可以从 $B$ 中推导出同一个空间的新基，该基具有相互正交的成员。对于新基的第一个成员，我们只需使用 ${\vec {\beta }}_{1}$。

${\vec {\kappa }}_{1}={\begin{pmatrix}4\\2\end{pmatrix}}$

对于新基的第二个成员，我们从 ${\vec {\beta }}_{2}$ 中减去其在 ${\vec {\kappa }}_{1}$ 方向上的部分，

$\displaystyle {\vec {\kappa }}_{2}={\begin{pmatrix}1\\3\end{pmatrix}}-{\mbox{proj}}_{\scriptstyle [{\vec {\kappa }}_{1}]}({\begin{pmatrix}1\\3\end{pmatrix}})={\begin{pmatrix}1\\3\end{pmatrix}}-{\begin{pmatrix}2\\1\end{pmatrix}}={\begin{pmatrix}-1\\2\end{pmatrix}}$

这留下了上面图示的 ${\vec {\kappa }}_{2}$ 部分，它是 ${\vec {\beta }}_{2}$ 的一部分，它与 ${\vec {\kappa }}_{1}$ 正交（根据投影到 ${\vec {\kappa }}_{1}$ 的跨度上的定义，它是正交的）。请注意，根据推论，$\{{\vec {\kappa }}_{1},{\vec {\kappa }}_{2}\}$ 是 $\mathbb {R} ^{2}$ 的基。

定义 2.5

向量空间的正交基是指由相互正交的向量组成的基。

示例 2.6

为了将 $\mathbb {R} ^{3}$ 的

$\left\langle {\begin{pmatrix}1\\1\\1\end{pmatrix}},{\begin{pmatrix}0\\2\\0\end{pmatrix}},{\begin{pmatrix}1\\0\\3\end{pmatrix}}\right\rangle$

转换成正交基，我们将第一个向量保留原样。

${\vec {\kappa }}_{1}={\begin{pmatrix}1\\1\\1\end{pmatrix}}$

我们通过从给定的第二个向量 ${\vec {\beta }}_{2}$ 开始，并减去其在 ${\vec {\kappa }}_{1}$ 方向上的部分来获得 ${\vec {\kappa }}_{2}$。

${\vec {\kappa }}_{2}={\begin{pmatrix}0\\2\\0\end{pmatrix}}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({\begin{pmatrix}0\\2\\0\end{pmatrix}})={\begin{pmatrix}0\\2\\0\end{pmatrix}}-{\begin{pmatrix}2/3\\2/3\\2/3\end{pmatrix}}={\begin{pmatrix}-2/3\\4/3\\-2/3\end{pmatrix}}$

最后，我们得到了 ${\vec {\kappa }}_{3}$，方法是取第三个给定的向量，并减去它在 ${\vec {\kappa }}_{1}$ 方向上的分量，以及它在 ${\vec {\kappa }}_{2}$ 方向上的分量。

${\vec {\kappa }}_{3}={\begin{pmatrix}1\\0\\3\end{pmatrix}}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({\begin{pmatrix}1\\0\\3\end{pmatrix}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({\begin{pmatrix}1\\0\\3\end{pmatrix}})={\begin{pmatrix}-1\\0\\1\end{pmatrix}}$

再次，推论表明

$\left\langle {\begin{pmatrix}1\\1\\1\end{pmatrix}},{\begin{pmatrix}-2/3\\4/3\\-2/3\end{pmatrix}},{\begin{pmatrix}-1\\0\\1\end{pmatrix}}\right\rangle$

是该空间的一个基。

下一个结果验证了在这些例子中使用的方法适用于 $\mathbb {R} ^{n}$ 的任何子空间的任何基（我们仅限于 $\mathbb {R} ^{n}$，因为我们还没有给出其他向量空间的正交性定义）。

定理 2.7（Gram-Schmidt 正交化）

如果 $\left\langle {\vec {\beta }}_{1},\ldots {\vec {\beta }}_{k}\right\rangle$ 是 $\mathbb {R} ^{n}$ 的一个子空间的基，则，其中

${\begin{array}{rl}{\vec {\kappa }}_{1}&={\vec {\beta }}_{1}\\{\vec {\kappa }}_{2}&={\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}})\\{\vec {\kappa }}_{3}&={\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}})\\&\vdots \\{\vec {\kappa }}_{k}&={\vec {\beta }}_{k}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{k}})-\cdots -{\mbox{proj}}_{[{\vec {\kappa }}_{k-1}]}({{\vec {\beta }}_{k}})\end{array}}$

的${\vec {\kappa }}\,$构成同一个子空间的正交基。

证明

我们将使用归纳法来验证每个 ${\vec {\kappa }}_{i}$ 不为零，且位于 $\left\langle {\vec {\beta }}_{1},\ldots {\vec {\beta }}_{i}\right\rangle$ 的张成空间内，并且与所有前面的向量正交： ${\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{i}=\cdots ={\vec {\kappa }}_{i-1}\cdot {\vec {\kappa }}_{i}=0$。结合这些，以及 推论 2.3，我们将得到 $\left\langle {\vec {\kappa }}_{1},\ldots {\vec {\kappa }}_{k}\right\rangle$ 是与 $\left\langle {\vec {\beta }}_{1},\ldots {\vec {\beta }}_{k}\right\rangle$ 相同的空间的基。

我们将讨论直到 $i=3$ 的情况，这将有助于理解这个论证。完成细节是 问题 15。

当 $i=1$ 时，这个情况是平凡的——设置 ${\vec {\kappa }}_{1}$ 等于 ${\vec {\beta }}_{1}$ 使其成为一个非零向量，因为 ${\vec {\beta }}_{1}$ 是基中的一个成员，它显然位于所需的张成空间中，并且“与所有前面的向量正交”的条件是空虚成立的。

对于 $i=2$ 的情况，展开 ${\vec {\kappa }}_{2}$ 的定义。

${\vec {\kappa }}_{2}={\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}})={\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\kappa }}_{1}={\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}$

这个展开式表明 ${\vec {\kappa }}_{2}$ 不为零，否则这将是在 ${\vec {\beta }}$ 之间的非平凡线性依赖关系（因为 ${\vec {\beta }}_{2}$ 的系数为 $1$）。它也表明 ${\vec {\kappa }}_{2}$ 在我们期望的生成空间中。最后， ${\vec {\kappa }}_{2}$ 与它前面唯一的向量正交

${\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{2}={\vec {\kappa }}_{1}\cdot ({\vec {\beta }}_{2}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{2}}))=0$

因为这个投影是正交的。

$i=3$ 的情况与 $i=2$ 的情况相同，除了一个细节。和 $i=2$ 的情况一样，展开定义

${\begin{array}{rl}{\vec {\kappa }}_{3}&={\vec {\beta }}_{3}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\kappa }}_{1}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{2}}{{\vec {\kappa }}_{2}\cdot {\vec {\kappa }}_{2}}}\cdot {\vec {\kappa }}_{2}\\&={\vec {\beta }}_{3}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}-{\frac {{\vec {\beta }}_{3}\cdot {\vec {\kappa }}_{2}}{{\vec {\kappa }}_{2}\cdot {\vec {\kappa }}_{2}}}\cdot {\bigl (}{\vec {\beta }}_{2}-{\frac {{\vec {\beta }}_{2}\cdot {\vec {\kappa }}_{1}}{{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{1}}}\cdot {\vec {\beta }}_{1}{\bigr )}\end{array}}$

表明${\vec {\kappa }}_{3}$ 不为零，并且在该空间内。计算表明${\vec {\kappa }}_{3}$ 与前面的向量${\vec {\kappa }}_{1}$ 正交。

${\begin{array}{rl}{\vec {\kappa }}_{1}\cdot {\vec {\kappa }}_{3}&={\vec {\kappa }}_{1}\cdot {\bigl (}{\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}})-{\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}}){\bigr )}\\&={\vec {\kappa }}_{1}\cdot {\bigl (}{\vec {\beta }}_{3}-{\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {\beta }}_{3}}){\bigr )}-{\vec {\kappa }}_{1}\cdot {\mbox{proj}}_{[{\vec {\kappa }}_{2}]}({{\vec {\beta }}_{3}})\\&=0\end{array}}$

(此处与 $i=2$ 的情况不同—第二行有两类项。第一项为零，因为此投影是正交的，如同在 $i=2$ 的情况下。第二项为零，因为 ${\vec {\kappa }}_{1}$ 与 ${\vec {\kappa }}_{2}$ 正交，因此也与 ${\vec {\kappa }}_{2}$ 所跨线的任何向量正交。）检查 ${\vec {\kappa }}_{3}$ 是否也与另一个前一个向量 ${\vec {\kappa }}_{2}$ 正交类似。

除了使基向量正交之外，我们还可以做更多；我们可以通过将每个向量除以其自身的长度来使每个向量长度为一（我们可以对长度进行 **归一化**）。

示例 2.8

对 示例 2.6 中正交基的每个向量进行长度归一化，得到此 **标准正交基**。

$\left\langle {\begin{pmatrix}1/{\sqrt {3}}\\1/{\sqrt {3}}\\1/{\sqrt {3}}\end{pmatrix}},{\begin{pmatrix}-1/{\sqrt {6}}\\2/{\sqrt {6}}\\-1/{\sqrt {6}}\end{pmatrix}},{\begin{pmatrix}-1/{\sqrt {2}}\\0\\1/{\sqrt {2}}\end{pmatrix}}\right\rangle$

除了直观的吸引力和它与标准基${\mathcal {E}}_{n}$ 在 $\mathbb {R} ^{n}$ 中的类比，正交基还简化了一些计算。例如，参见 练习 9。

练习

问题 1

对 $\mathbb {R} ^{2}$ 的每个基执行 Gram-Schmidt 过程。

1. $\left\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}2\\1\end{pmatrix}}\right\rangle$
2. $\left\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}-1\\3\end{pmatrix}}\right\rangle$
3. $\left\langle {\begin{pmatrix}0\\1\end{pmatrix}},{\begin{pmatrix}-1\\0\end{pmatrix}}\right\rangle$

然后将这些正交基转换为标准正交基。

建议所有读者完成此练习。

问题 2

对 $\mathbb {R} ^{3}$ 的每个基执行 Gram-Schmidt 过程。

1. $\left\langle {\begin{pmatrix}2\\2\\2\end{pmatrix}},{\begin{pmatrix}1\\0\\-1\end{pmatrix}},{\begin{pmatrix}0\\3\\1\end{pmatrix}}\right\rangle$
2. $\left\langle {\begin{pmatrix}1\\-1\\0\end{pmatrix}},{\begin{pmatrix}0\\1\\0\end{pmatrix}},{\begin{pmatrix}2\\3\\1\end{pmatrix}}\right\rangle$

然后将这些正交基转换为标准正交基。

建议所有读者完成此练习。

问题 3

找到 $\mathbb {R} ^{3}$ 的这个子空间的标准正交基：平面 $x-y+z=0$。

问题 4

找到 $\mathbb {R} ^{4}$ 的这个子空间的标准正交基。

$\{{\begin{pmatrix}x\\y\\z\\w\end{pmatrix}}\,{\big |}\,x-y-z+w=0{\text{ and }}x+z=0\}$

问题 5

证明 $\mathbb {R} ^{n}$ 中的任何线性无关子集都可以正交化，而不会改变其跨度。

建议所有读者完成此练习。

问题 6

如果我们将 Gram-Schmidt 正交化过程应用于一个已经正交的基，会发生什么？

问题 7

令 $\left\langle {\vec {\kappa }}_{1},\dots ,{\vec {\kappa }}_{k}\right\rangle$ 是 $\mathbb {R} ^{n}$ 中的一组互相正交的向量。

1. 证明对于空间中的任何 ${\vec {v}}$，向量 ${\vec {v}}-({\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {v}}_{k}]}({{\vec {v}}\,}))$ 与 ${\vec {\kappa }}_{1}$，…，${\vec {\kappa }}_{k}$ 中的每一个正交。
2. 用 ${\vec {e}}_{1}$ 作为 ${\vec {\kappa }}_{1}$，用 ${\vec {e}}_{2}$ 作为 ${\vec {\kappa }}_{2}$，并将 ${\vec {v}}$ 的分量设置为 $1$，$2$ 和 $3$ 在 $\mathbb {R} ^{3}$ 中说明前一个项目。
3. 证明 ${\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {v}}_{k}]}({{\vec {v}}\,})$ 是 ${\vec {\kappa }}$ 集合的跨度中最接近 ${\vec {v}}$ 的向量。提示：在前一部分的图示中，添加向量 $d_{1}{\vec {\kappa }}_{1}+d_{2}{\vec {\kappa }}_{2}$ 并将毕达哥拉斯定理应用于所得三角形。

问题 8

在 $\mathbb {R} ^{3}$ 中找到一个与这两个向量都正交的向量。

${\begin{pmatrix}1\\5\\-1\end{pmatrix}}\qquad {\begin{pmatrix}2\\2\\0\end{pmatrix}}$

建议所有读者完成此练习。

问题 9

正交基的一个优点是它们简化了寻找向量相对于该基的表示。

1. 对于此向量和此非正交基，用于 $\mathbb {R} ^{2}$

   ${\vec {v}}={\begin{pmatrix}2\\3\end{pmatrix}}\qquad B=\left\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}1\\0\end{pmatrix}}\right\rangle$

   首先，将向量相对于基表示出来。然后将向量投影到每个基向量 $[{{\vec {\beta }}_{1}}]$ 和 $[{{\vec {\beta }}_{2}}]$ 的跨度上。
2. 对于 $\mathbb {R} ^{2}$ 的这个正交基

   $K=\left\langle {\begin{pmatrix}1\\1\end{pmatrix}},{\begin{pmatrix}1\\-1\end{pmatrix}}\right\rangle$

   用相同的向量 ${\vec {v}}$ 相对于基表示出来。然后将向量投影到每个基向量的跨度上。请注意，表示和投影中的系数是相同的。
3. 令 $K=\left\langle {\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{k}\right\rangle$ 为 $\mathbb {R} ^{n}$ 的某个子空间的正交基。证明对于子空间中的任何 ${\vec {v}}$，表示 ${\rm {Rep}}_{K}({\vec {v}}\,)$ 的第 $i$ 个分量是来自 ${\mbox{proj}}_{[{\vec {\kappa }}_{i}]}({{\vec {v}}\,})$ 的标量系数 $({\vec {v}}\cdot {\vec {\kappa }}_{i})/({\vec {\kappa }}_{i}\cdot {\vec {\kappa }}_{i})$。
4. 证明 ${\vec {v}}={\mbox{proj}}_{[{\vec {\kappa }}_{1}]}({{\vec {v}}\,})+\dots +{\mbox{proj}}_{[{\vec {\kappa }}_{k}]}({{\vec {v}}\,})$。

问题 10

贝塞尔不等式。考虑以下正交集

$B_{1}=\{{\vec {e}}_{1}\}\quad B_{2}=\{{\vec {e}}_{1},{\vec {e}}_{2}\}\quad B_{3}=\{{\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}\}\quad B_{4}=\{{\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3},{\vec {e}}_{4}\}$

以及向量 ${\vec {v}}\in \mathbb {R} ^{4}$，其分量为 $4$，$3$，$2$ 和 $1$。

1. 找到 ${\vec {v}}$ 向 $B_{1}$ 中向量所张成的空间的投影的系数 $c_{1}$。验证 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}$。
2. 找到 ${\vec {v}}$ 向 $B_{2}$ 中两个向量所张成的空间的投影的系数 $c_{1}$ 和 $c_{2}$。验证 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+|c_{2}|^{2}$。
3. 找到与向量 $B_{3}$ 中相关的 $c_{1}$、$c_{2}$ 和 $c_{3}$，以及与向量 $B_{4}$ 中相关的 $c_{1}$、$c_{2}$、$c_{3}$ 和 $c_{4}$。检查 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+\dots +|c_{3}|^{2}$ 和 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+\dots +|c_{4}|^{2}$。

证明一般情况下成立：其中 $\{{\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{k}\}$ 是一个标准正交集，而 $c_{i}$ 是向量 ${\vec {v}}$ 在该空间上的投影的系数，则 $|{\vec {v}}\,|^{2}\geq |c_{1}|^{2}+\dots +|c_{k}|^{2}$。提示。一种方法是观察不等式 $0\leq |{\vec {v}}-(c_{1}{\vec {\kappa }}_{1}+\dots +c_{k}{\vec {\kappa }}_{k})|^{2}$ 并展开 $c$。

问题 11

证明或反驳：$\mathbb {R} ^{n}$ 中的每个向量都属于某个正交基。

问题 12

证明一个 $n\!\times \!n$ 矩阵的列向量构成一个正交集当且仅当该矩阵的逆矩阵等于其转置。并给出这样一个矩阵。

问题 13

在 定理 2.2 的证明中，是否忽略了向量集为空的可能性（即 $k=0$）？

问题 14

定理 2.7 描述了从任何基 $B=\left\langle {\vec {\beta }}_{1},\ldots ,{\vec {\beta }}_{k}\right\rangle$ 到正交基 $K=\left\langle {\vec {\kappa }}_{1},\ldots ,{\vec {\kappa }}_{k}\right\rangle$ 的变换。考虑变换矩阵 ${\rm {Rep}}_{B,K}({\mbox{id}})$。

1. 证明矩阵 ${\rm {Rep}}_{K,B}({\mbox{id}})$ （与定理中变换方向相反的基变换）是上三角矩阵，即主对角线以下的所有元素都为零。
2. 证明上三角矩阵的逆矩阵也是上三角矩阵（如果该矩阵可逆）。这表明矩阵 ${\rm {Rep}}_{B,K}({\mbox{id}})$ （按定理中描述的变换方向的基变换）是上三角矩阵。

问题 15

完成 定理 2.7 证明中的归纳论证。

解答