线性代数/主题：射影几何

线性代数
← 主题：计算行列式的速度	主题：射影几何	相似性的介绍 →

除了我们熟悉的欧几里得几何之外，还有其他几何。这种几何出现在艺术中，人们观察到，观察者所看到的不一定是存在的。这是列奥纳多·达·芬奇的《最后的晚餐》。

例如，房间里天花板与左右墙壁交汇的地方实际上是平行线。然而，观察者所看到的是几条线，如果延长，它们将会相交。交点被称为*消失点*。透视的这种方面也很熟悉，比如长长的铁轨看起来汇聚在远处的图像。

为了描绘房间，达·芬奇采用了我们如何观察、如何将三维场景投射到二维图像的模型。这个模型只是一个第一近似——它没有考虑我们的视网膜是弯曲的，我们的晶状体弯曲了光线，我们具有双眼视觉，以及我们的大脑处理过程极大地影响了我们所看到的东西——但尽管如此，它仍然很有趣，既有艺术意义，也有数学意义。

投影不是正交的，它是一个从单个点到画布平面的*中心投影*。

(它不是正交投影，因为从观察者到 $C$ 的直线不正交于图像平面。) 正如图像所示，中心投影操作保留了一些几何属性——直线投射到直线。然而，它没有保留其他一些属性——等长的线段可以投射到不等长的线段； $AB$ 的长度大于 $BC$ 的长度，因为投影到 $AB$ 的线段更靠近观察者，更靠近的东西看起来更大。研究中心投影的影响就是射影几何。我们将看到线性代数如何在这项研究中使用。

中心投影有三种情况。第一种是由电影放映机完成的投影。

我们可以认为每个源点都从定义域平面向外“推动”到共域平面中的像点。这种投影方式与第二种情况有所不同，第二种情况是艺术家将源点“拉回”到画布上。

在第一种情况下， $S$ 在中间，而在第二种情况下， $I$ 在中间。还可以使用另一种配置， $P$ 在中间。一个例子就是我们使用针孔将日食的图像照射到一张纸上。

我们将把这三种情况都视为 $P$ 对 $S$ 到 $I$ 的中心投影。

再次考虑铁轨看起来汇聚到一点的影响。我们用定义域平面 $S$ 中的平行线和通过 $P$ 到共域平面 $I$ 的投影来模拟这种现象（灰色线平行于 $S,I$ ）.

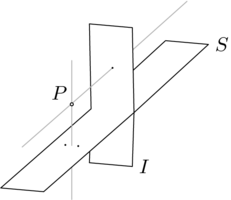
这里展示了所有三种投影情况。下面的第一张图片展示了 $P$ 像电影放映机一样，将 $S$ 的一部分的点投影到 $I$ 的下半部分的像点。中间的图片展示了 $P$ 像艺术家一样，将 $S$ 的另一部分的点拉回到 $I$ 的中间的像点。在第三张图片中， $P$ 像针孔一样，将 $S$ 的点投影到 $I$ 的上半部分。这幅图是最难理解的 - 投影到消失点附近的点是那些在 $S$ 的左下角最远处的点。在 $S$ 中靠近垂直灰色线的点被投影到 $I$ 的高处。

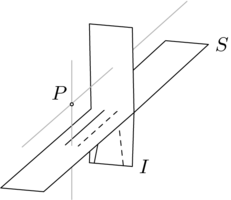
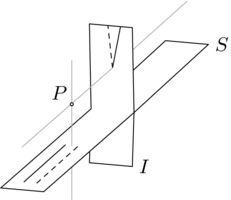
这种情况有两个尴尬的地方。第一个是，域中两个最靠近垂直灰色线的点都没有像，因为从这两个点进行的投影是沿着与陪域平面平行的灰色线进行的（我们有时说这两个点被投影“到无穷远”）。第二个尴尬的地方是， $I$ 中的消失点不是来自 $S$ 的任何点的像，因为对该点的投影将沿着与域平面平行的灰色线进行（我们有时说消失点是“来自无穷远”的投影的像）。

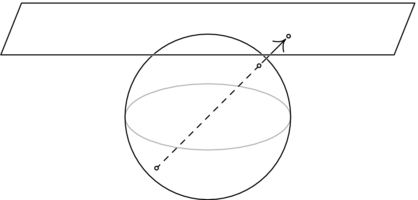
为了获得更好的模型，将投影仪 $P$ 放在原点。想象一下 $P$ 被一个玻璃半球形圆顶覆盖。当 $P$ 向外看时，视线中的任何物体都会投射到圆顶上的同一个点。这包括 $P$ 和圆顶之间的线上的物体，例如电影投影仪的投影。它还包括距离 $P$ 比圆顶更远的线上的物体，例如画家进行投影的情况。它还包括位于 $P$ 后面的线上的物体，例如针孔投影的情况。

从这个角度看 $P$ ，线上的所有点都被视为同一个点。因此，对于任何非零向量 ${\vec {v}}\in \mathbb {R} ^{3}$ ，我们定义相关的 投影平面上的点 $v$ 为集合 ${\bigl \{}k{\vec {v}}:k\in \mathbb {R} ,k\neq 0{\bigr \}}$ ，该集合包含所有非零向量，这些向量与 ${\vec {v}}$ 在通过原点的同一条直线上。为了描述一个投影点，我们可以给出这条直线的任何代表成员，因此上面显示的投影点可以用以下三种方式中的任何一种表示。

{\begin{pmatrix}1\\2\\3\end{pmatrix}}\qquad {\begin{pmatrix}{\frac {1}{3}}\\{\frac {2}{3}}\\1\end{pmatrix}}\qquad {\begin{pmatrix}-2\\-4\\-6\end{pmatrix}}

这些都是 $v$ 的 齐次坐标向量。

这幅图以及它所产生的上述定义澄清了中心投影的描述，但圆顶模型中存在一些令人困惑的地方：如果观察者向下看会怎样？如果我们画出 $P$ 的视线，使得视线朝着我们，即离开页面的一端，向下延伸到圆顶下方，然后我们可以沿视线方向向后追踪，向上越过 $P$ ，朝向半球背面，即页面后面的部分。因此，在圆顶模型中，向下看会得到一个位于观察者身后的投影点。因此，如果上图中的观察者将视线降至圆顶底部，那么投影点也会下降，并且随着视线继续向下延伸穿过赤道，投影点会突然从圆顶正面转移到圆顶背面。这种图纸上的不连续性意味着我们通常需要将赤道点视为一个单独的案例。也就是说，虽然中心投影的铁路轨道讨论有三种情况，但圆顶模型只有两种。

我们可以做得更好。考虑一个以原点为中心的球体。通过原点的任何直线都与球体相交于两点，这两点被称为对映点。因为我们将通过原点的每条直线与投影平面上的一个点相关联，所以我们可以将这样的点绘制为球体上的两个对映点。在下图中，这两个对映点用虚线连接，以强调它们不是两个不同的点，这两个点的组合构成一个投影点。

虽然将点绘制为一对对映点不如每点一个点的圆顶模型自然，但另一方面，圆顶模型的尴尬之处消失了，因为当视线从北向南滑动时，图像上不会出现突然的变化。这种中心投影模型是均匀的——三种情况简化为一种。

到目前为止，我们已经描述了投影几何中的点。那么线呢？观察者在原点看到的直线在下图中显示为一个大圆，即模型球体与通过原点的平面相交的部分。

(这条直线上的一个投影点显示出一种微妙之处。因为两个对映点组合构成一个投影点，所以大圆的页面背面部分与页面正面部分是同一组投影点。) 正如我们对每个投影点所做的那样，我们也将用三个实数来描述投影直线。例如，通过 $\mathbb {R} ^{3}$ 中的原点的这个平面中的成员

\left\{{\begin{pmatrix}x\\y\\z\end{pmatrix}}:x+y-z=0\right\}

投影到一条可以用三重数 $(1\ 1\ -1)$ 描述的直线上（我们使用行向量在排版上区分直线和点）。一般来说，对于任何非零的三维行向量 ${\vec {L}}$ ，我们将与之关联的投影平面上的直线定义为集合 $L={\bigl \{}k{\vec {L}}:k\in \mathbb {R} ,k\neq 0{\bigr \}}$ ，它是由 ${\vec {L}}$ 的非零倍数组成的。

将直线描述为三元组的原因在于，在射影平面中，点 $v$ 和直线 $L$ 是 **关联** 的——点在直线上，直线经过点——当且仅当它们的代表向量 $v_{1}L_{1}+v_{2}L_{2}+v_{3}L_{3}$ 的点积为零（问题 4 表明这与代表向量 ${\vec {v}}$ 和 ${\vec {L}}$ 的选择无关）。例如，上面由分量为 $1,2,3$ 的列向量描述的射影点位于由 $(1\ 1\ -1)$ 描述的射影直线上，仅仅是因为 $\mathbb {R} ^{3}$ 中任何分量比例为 $1:2:3$ 的向量都位于通过原点的平面上，其方程形式为 $1k\cdot x+1k\cdot y-1k\cdot z=0$ ，其中 $k$ 为非零值。也就是说，关联公式是 $v$ 和 $L$ 是三维空间中的直线和平面投影的结果。

因此，我们可以进行解析射影几何。例如，射影直线 $L=(1\ 1\ -1)$ 的方程为 $1v_{1}+1v_{2}-1v_{3}=0$ ，因为位于直线上的点都具有其代表向量满足此方程的性质。与熟悉的欧几里德解析几何不同的是，在射影几何中我们讨论的是点的方程。对于一个固定的点，例如

v={\begin{pmatrix}1\\2\\3\end{pmatrix}}

通过该点的直线（即与该点相交的直线）的特征是，任何代表直线的向量的分量都满足 $1L_{1}+2L_{2}+3L_{3}=0$ ，因此，这就是 $v$ 的方程。

关于直线和点的陈述的对称性揭示了射影几何的对偶原理：在任何真命题中，将“点”与“直线”互换，得到的仍然是一个真命题。例如，正如两点确定一条直线，在射影平面上，两条直线确定一个点。下图显示了两条直线在对跖点相交，因此在射影平面上相交于一个点。

$(*)$

将此与欧几里得几何进行对比，在欧几里得几何中，两条不同的直线可能有一个唯一的交点，也可能平行。这样，射影几何比欧几里得几何更简单、更统一。

这种简单性很重要，因为欧几里得几何和射影几何之间存在联系：射影平面可以看作是欧几里得平面的扩展。以球面模型表示射影平面，即 $\mathbb {R} ^{3}$ 中的单位球，并将欧几里得空间视为平面 $z=1$ 。这使我们能够将射影空间中的某些点视为对应于欧几里得空间中的点，因为平面上所有点都是球面上对跖点的投影。

$(**)$

注意，赤道上的射影点不会投影到平面上。相反，它们投影到“无穷远”。因此，我们可以认为射影空间由欧几里得平面加上一些附加点组成——欧几里得平面嵌入在射影平面上。这些附加点，即赤道上的点，被称为理想点或无穷远点，而赤道被称为理想线或无穷远线（注意，它不是欧几里得直线，而是一条射影直线）。

扩展到射影平面的优势在于，欧几里得几何中的一些尴尬之处消失了。例如，上面在 $(*)$ 中所示的射影直线在球面赤道上，即对跖点处，相交于一个射影点。如果我们将这些直线放入 $(**)$ 中，它们对应于欧几里得几何中的平行直线。也就是说，从欧几里得平面到射影平面的变换，将直线相交或平行两种情况，统一成了直线相交（可能在无穷远点相交）一种情况。

在许多方面，射影几何比欧几里得几何更“优雅”，但问题在于我们对它没有相同的经验或直觉。这是做解析几何的一个优势，解析几何中方程可以引导我们得出正确的结论。解析射影几何使用线性代数。例如，对于射影平面上的三个点 $t,u,v$ ，通过固定表示每个点的向量，建立这些点的方程，可以看出，当且仅当由此得到的三个方程组有无穷多个表示该直线的行向量解时，这三个点是共线的——位于一条直线上。而这又等价于以下行列式为零。

{\begin{vmatrix}t_{1}&u_{1}&v_{1}\\t_{2}&u_{2}&v_{2}\\t_{3}&u_{3}&v_{3}\end{vmatrix}}

因此，射影平面上的三个点是共线的，当且仅当任何三个代表它们的列向量线性相关。类似地（这也说明了对偶原理），射影平面上的三条直线交于一点，当且仅当任何三个表示它们的列向量线性相关。

以下结果进一步证明了射影平面几何的“优雅”，与欧几里得几何相比。这两个三角形被称为从 $P$ 透视，因为它们的对应顶点是共线的。

考虑对应边的配对：边 $T_{1}U_{1},T_{2}U_{2}$ ，边 $T_{1}V_{1},T_{2}V_{2}$ ，以及边 $U_{1}V_{1},U_{2}V_{2}$ 。德萨格定理指出，当三对对应边延伸成直线时，它们会相交（这里显示为点 $TU$ ，点 $TV$ ，以及点 $UV$ ）, 而且，这三个交点是共线的。

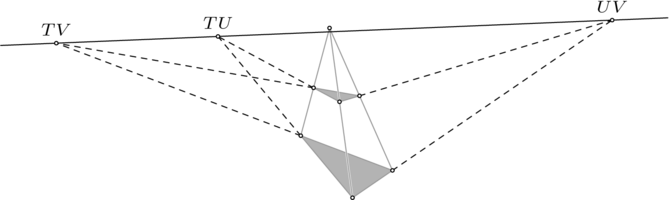
我们将使用射影几何来证明这个定理。（这些被画成了欧几里得图形，因为这是更熟悉的图像。为了将它们视为射影图形，我们可以想象，尽管所示的线段是圆弧的一部分，并且是弯曲的，但模型的半径与图形大小相比非常大，因此，在这个草图中，边看起来是直的。）

对于这个证明，我们需要一个初步的引理 (Coxeter 1974)：如果 $W,X,Y,Z$ 是射影平面上的四个点（其中没有三个点是共线的），那么存在射影点的齐次坐标向量 ${\vec {w}},{\vec {x}},{\vec {y}},{\vec {z}}$ ，以及 $\mathbb {R} ^{3}$ 的基 $B$ ，满足以下条件。

{\text{Rep}}_{B}({\vec {w}})={\begin{pmatrix}1\\0\\0\end{pmatrix}}\quad {\text{Rep}}_{B}({\vec {x}})={\begin{pmatrix}0\\1\\0\end{pmatrix}}\quad {\text{Rep}}_{B}({\vec {y}})={\begin{pmatrix}0\\0\\1\end{pmatrix}}\quad {\text{Rep}}_{B}({\vec {z}})={\begin{pmatrix}1\\1\\1\end{pmatrix}}

证明很简单。因为 $W,X,Y$ 不在同一条射影线上，任何齐次坐标向量 ${\vec {w}}_{0},{\vec {x}}_{0},{\vec {y}}_{0}$ 不在 $\mathbb {R} ^{3}$ 中通过原点的同一平面上，因此构成 $\mathbb {R} ^{3}$ 的一个生成集。因此， $Z$ 的任何齐次坐标向量都可以写成组合 ${\vec {z}}_{0}=a{\vec {w}}_{0}+b{\vec {x}}_{0}+c{\vec {y}}_{0}$ 。然后，我们可以取

{\begin{aligned}{\vec {w}}&=a{\vec {w}}_{0}\\{\vec {x}}&=b{\vec {x}}_{0}\\{\vec {y}}&=c{\vec {y}}_{0}\\{\vec {z}}&={\vec {z}}_{0}\end{aligned}}

其中基为 $B=\langle {\vec {w}},{\vec {x}},{\vec {y}}\rangle$ 。

现在，为了证明德萨格定理，使用引理来固定齐次坐标向量和基。

{\text{Rep}}_{B}({\vec {t}}_{1})={\begin{pmatrix}1\\0\\0\end{pmatrix}}\quad {\text{Rep}}_{B}({\vec {u}}_{1})={\begin{pmatrix}0\\1\\0\end{pmatrix}}\quad {\text{Rep}}_{B}({\vec {v}}_{1})={\begin{pmatrix}0\\0\\1\end{pmatrix}}\quad {\text{Rep}}_{B}({\vec {o}})={\begin{pmatrix}1\\1\\1\end{pmatrix}}

因为投影点 $T_{2}$ 与投影线 $OT_{1}$ 相交，则 $T_{2}$ 的任何齐次坐标向量都位于 $\mathbb {R} ^{3}$ 中以原点为起点，由 $O$ 和 $T_{1}$ 的齐次坐标向量所跨越的平面上。

{\text{Rep}}_{B}({\vec {t}}_{2})=a{\begin{pmatrix}1\\1\\1\end{pmatrix}}+b{\begin{pmatrix}1\\0\\0\end{pmatrix}}

对于一些标量 $a$ 和 $b$ 。也就是说，线 $OT_{1}$ 上的成员 $T_{2}$ 的齐次坐标向量形式如左下方所示，而 $U_{2},V_{2}$ 的形式类似。

{\text{Rep}}_{B}({\vec {t}}_{2})={\begin{pmatrix}t_{2}\\1\\1\end{pmatrix}}\qquad {\text{Rep}}_{B}({\vec {u}}_{2})={\begin{pmatrix}1\\u_{2}\\1\end{pmatrix}}\qquad {\text{Rep}}_{B}({\vec {v}}_{2})={\begin{pmatrix}1\\1\\v_{2}\end{pmatrix}}

投影线 $T_{1}U_{1}$ 是 $\mathbb {R} ^{3}$ 中过原点的平面的像。一个快速获得其方程的方法是注意到其中的任何向量都线性依赖于 $T_{1}$ 和 $U_{1}$ 的向量，因此该行列式为零。

{\begin{vmatrix}1&0&x\\0&1&y\\0&0&z\end{vmatrix}}=0\qquad \implies \qquad z=0

在 $\mathbb {R} ^{3}$ 中，其像为投影线 $T_{2}U_{2}$ 的平面的方程如下。

{\begin{vmatrix}t_{2}&1&x\\1&u_{2}&y\\1&1&z\end{vmatrix}}=0\qquad \implies \qquad (1-u_{2})x+(1-t_{2})y+(t_{2}u_{2}-1)z=0

找到这两个的交点是例行的。

T_{1}U_{1}\cap T_{2}U_{2}={\begin{pmatrix}t_{2}-1\\1-u_{2}\\0\end{pmatrix}}

(当然，这是投影点的齐次坐标向量。)另外两个交点类似。

T_{1}V_{1}\cap T_{2}V_{2}={\begin{pmatrix}1-t_{2}\\0\\v_{2}-1\end{pmatrix}}\qquad U_{1}V_{1}\cap U_{2}V_{2}={\begin{pmatrix}0\\u_{2}-1\\1-v_{2}\end{pmatrix}}

证明通过注意到这些投影点位于同一条投影线上而完成，因为三个齐次坐标向量的和为零。

每个射影定理都可以转化为欧几里得版本，虽然欧几里得结果在陈述和证明上通常更复杂。德扎格定理就很好地说明了这一点。在转化为欧几里得空间时，当 $O$ 位于理想线上时，必须单独处理，因为此时直线 $T_{1}T_{2},U_{1}U_{2},V_{1}V_{2}$ 平行。

德扎格定理陈述后面的括号备注建议将欧几里得图像视为射影几何中的图形，以作为半径非常大的模型。也就是说，正如地球上的一个小区域对居住在那里的人来说看起来是平坦的，射影平面也是“局部欧几里得”的。

虽然射影平面的局部性质是熟悉的欧几里得性质，但它有一个全局性质与欧几里得性质完全不同。下面的图片显示了一个射影点。在这个点上画了一个 $xy$ -轴。这个轴在球体的对极端点处出现的形式非常有趣。在北半球，轴以黑色绘制，右手将手指放在 $x$ -轴上，拇指将指向 $y$ -轴。但对极轴正好相反：将右手放在 $x$ -轴上，拇指将指向错误的方向，相反，是左手才能正常运作。简而言之，射影平面不可定向：在这种几何中，左右手性不是图形的固定属性。

下面的一系列图片戏剧性地展现了这种不可定向性。它们描绘了沿 $y$ 部分的 $xy$ -轴在这个空间中旅行。（警告：显示的旅行不是半圈，而是全圈。诚然，如果我们把这个变成电影，那么我们可以看到上面图画中北半球的点逐渐绕球体旋转大约半圈，到达下面最后一张图片。而且我们可以看到上面图片中南半球的点滑过南极，向上穿过赤道，到达最后一张图片。但是：虚线两端点的点是同一个射影点。我们不需要继续走很远；到最后一张图片时，我们几乎回到了开始的射影点。）

$\implies$ $\implies$

在回路结束时， $x$ 部分的 $xy$ -轴以相反的方向伸出。因此，在射影平面中，我们无法将图形描述为右手或左手（另一种表达方式是我们无法将螺旋线描述为顺时针或逆时针）。

这种非定向空间存在的展示提出了一个问题，即我们的宇宙是否可定向：宇航员是否有可能以右手状态离开，以左手状态返回？一个很好的非技术参考是 (Gardner 1990)。关于方向反转的经典科幻故事是 (Clarke 1982)。

所以射影几何在数学上很有趣，除了它在艺术中自然出现的形式之外。它不仅仅是缩短某些证明的技术手段。有关概述，请参见 (Courant & Robbins 1978)。我们在这里采用的方法，即分析方法，可以得出快速定理，而且——对我们来说最重要的是——它说明了线性代数的力量（参见 Hanes (1990), Ryan (1986), 和 Eggar (1998))。但是，另一种方法，即从公理系统推导出结果的合成方法，既极其美妙，也是发展的历史路线。两种关于这种方法的优秀来源是 (Coxeter 1974) 或 (Seidenberg 1962)。一个有趣且容易的应用是 (Davies 1990)。

练习

问题 1

这个点的方程是什么？

{\begin{pmatrix}1\\0\\0\end{pmatrix}}

问题 2

在射影平面上找到经过这两个点的直线。
${\begin{pmatrix}1\\2\\3\end{pmatrix}},{\begin{pmatrix}4\\5\\6\end{pmatrix}}$
找到同时经过这两条射影直线的点。
$(1\ 2\ 3),(4\ 5\ 6)$

问题 3

找出经过两个射影点的直线的公式。找出经过两个射影直线的点的公式。

问题 4

证明入射定义与 $p$ 和 $L$ 代表的选择无关。也就是说，如果 $p_{1},p_{2},p_{3}$ 和 $q_{1},q_{2},q_{3}$ 是 $p$ 的两个齐次坐标三元组，而 $L_{1},L_{2},L_{3}$ 和 $M_{1},M_{2},M_{3}$ 是 $L$ 的两个齐次坐标三元组，证明 $p_{1}L_{1}+p_{2}L_{2}+p_{3}L_{3}=0$ 当且仅当 $q_{1}M_{1}+q_{2}M_{2}+q_{3}M_{3}=0$ 。

问题 5

画图说明中心投影不保持圆形，圆形可能投影成椭圆形。一个（非圆形）椭圆形可以投影成圆形吗？

问题 6

给出射影平面反极点模型的非赤道部分与平面 $z=1$ 之间的对应公式。

问题 7

(帕普斯定理) 假设 $T_{0},U_{0},V_{0}$ 是共线的，并且 $T_{1},U_{1},V_{1}$ 也是共线的。考虑以下三个点

直线 $T_{0}U_{1},T_{1}U_{0}$ 的交点 $V_{2}$
直线 $T_{0}V_{1},T_{1}V_{0}$ 的交点 $U_{2}$
直线 $U_{0}V_{1}$ 和 $U_{1}V_{0}$ 的交点 $T_{2}$

画一个（欧几里得）图形。
应用德萨格定理中使用的引理，为 $T$ 和 $V_{0}$ 获取简单的齐次坐标向量。
找到 $U$ 的结果齐次坐标向量（这些向量必须包含一个参数，例如， $U_{0}$ 可以位于 $T_{0}V_{0}$ 线上的任何位置）。
找到 $V_{1}$ 的结果齐次坐标向量。（提示：它包含两个参数。）
找到 $V_{2}$ 的结果齐次坐标向量。（它也包含两个参数。）
证明三个参数的乘积为 1。
验证 $V_{2}$ 是否在 $T_{2}U_{2}$ 直线上。

解决方案

另见

参考文献

克拉克，亚瑟·C. (1982), 伟大的科幻故事 8：技术错误, DAW Books.
库朗，理查德；罗宾斯，赫伯特 (1978), 什么是数学？, 牛津大学出版社.
考克斯特，H.S.M. (1974), 射影几何 (第二版), 施普林格出版社.
戴维斯，托马斯·D. (1990), “新的证据表明皮尔里到达了北极”，国家地理杂志, 177 (1): 44 {{引用}}: 未知参数 |month= 被忽略 (帮助).
埃加，M.H. (1998), “针孔相机、透视和射影几何”，美国数学月刊, 美国数学学会: 618–630 {{引用}}: 未知参数 |month= 被忽略 (帮助).
加德纳，马丁 (1990), 新左右对称宇宙 (第三修订版), W. H. Freeman and Company.
汉斯，基特 (1990), “解析射影几何及其应用”，UMAP 模块 (UMAP UNIT 710): 111.
瑞安，帕特里克·J. (1986), 欧几里得和非欧几里得几何：解析方法, 剑桥大学出版社.
塞登伯格，A. (1962), 射影几何讲义, 范·诺斯特兰德.

线性代数
← 主题：计算行列式的速度	主题：射影几何	相似性的介绍 →