信号与系统/二阶传递函数

二阶传递函数是最简单的具有复极点的传递函数。对其进行分析可以回顾我们从模拟滤波器设计中获得的信息，并为实现二阶段级联滤波器提供一个良好的起点。

全极点二阶传递函数

传递函数

连续时间全极点二阶系统的传递函数为

H(s)={\frac {b_{0}}{s^{2}+a_{1}s+a_{0}}}

请注意， $s^{2}$ 的系数已设为 1。这在不损失一般性的情况下简化了书写，因为分子和分母可以乘以或除以相同的因子。

对于 $s=i\omega$ ，其频率响应具有直流幅度

H(i\omega =0)={\frac {b_{0}}{a_{0}}}

对于非常高的频率，分母中最重要的项是 $(i\omega )^{2}$ ，频率响应越来越接近

H(i\omega )\cong {\frac {b_{0}}{(i\omega )^{2}}}

在高频下，幅频响应在线性图中看起来像一个（平方）双曲线，在对数-对数图中看起来像一条具有负斜率的直线。将频率绘制在十年制中，幅度绘制在分贝中，则显示出 -40 [dB/十年] 的斜率。

在直流具有给定幅度，而在高频下幅度接近于零，表明传递函数是低通类型的。

极点

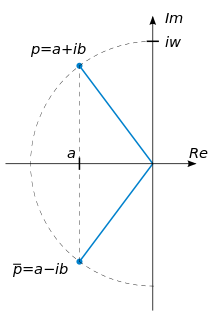
系统的极点由分母多项式的根给出

p,p^{*}={\frac {-a_{1}\pm {\sqrt {a_{1}^{2}-4a_{0}}}}{2}}

如果平方根内的项为负数，则极点为复共轭。这是滤波器设计中的普遍情况：人们对具有两个实极点的二阶传递函数没有太大的兴趣。

根据极点的位置，传递函数可以被重写为

H(s)={\frac {k}{(s-p)(s-p^{*})}}={\frac {k}{s^{2}-2Re(p)s+abs(p)^{2}}}

极点的幅度决定了滤波器的截止频率。截止频率定义为对数-对数幅频响应曲线中水平线和 -40 [dB/decade] 线相交点的横坐标。注意，这并不一定是滤波器的 -3 [dB] 衰减频率。

\omega _{0}=abs(p)={\sqrt {a_{0}}}

极点的实部与截止频率之比与系统的阻尼比成正比，或与系统的品质因数成反比。

\zeta ={\frac {-Re(p)}{\omega _{0}}}={\frac {a_{1}}{2\omega _{0}}}

Q={\frac {1}{2\zeta }}={\frac {\omega _{0}}{-2Re(p)}}={\frac {\omega _{0}}{a_{1}}}

极点越靠近虚轴，在小于但接近系统截止频率的频率处就越可能出现谐振。

传递函数重写

利用这些，直流增益为 1 的传递函数可以根据截止频率和阻尼比重写为以下形式

H(s)={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}\cdot s+\omega _{0}^{2}}}

$s$ 和 $\omega _{0}$ 的单位均为 [s^-1]。 $\zeta$ 的单位为 [1]，总传递函数的单位也是 [1]。

双二次二阶传递函数

传递函数

名称“双二次”源于该函数具有两个二阶多项式。

H(s)={\frac {b_{2}s^{2}+b_{1}s+b_{0}}{s^{2}+a_{1}s+a_{0}}}

极点

极点的分析方式与全极点二阶传递函数相同。它们决定了系统的截止频率和品质因数。

零点

零点用于影响幅频响应的形状。

将零点放在略高于截止频率的虚轴上，可以在阻带中获得更大的衰减，并使通带到阻带的过渡更快。这就是切比雪夫 II 型和椭圆滤波器函数的工作原理。
将零点精确地放在虚轴上的截止频率处，会迫使该特定点的幅度为零。这对应于带阻（或陷波）函数。
将单个零点放在 s 平面的 (0, 0) 坐标处会将函数转换为带通函数。可以通过将系数 $b_{2}=0$ 和 $b_{0}=0$ 来实现。
将两个零点都放在 (0, 0) 坐标处，将函数转换为高通函数。这可以通过设置系数 $b_{1}=0$ 和 $b_{0}=0$ 来实现。
将零点放在右半平面，关于极点对称，得到一个全通函数：虚轴上的任何点到零点和到相应极点的距离都相等。这个全通函数用于整形传递函数的相位响应。

示例

6阶归一化巴特沃斯滤波器

示例

本例分析了 6 阶归一化巴特沃斯滤波器的 3 个二阶部分。

巴特沃斯滤波器的极点在以复平面原点为中心的圆的左半部分上均匀分布。每个复共轭极点对构成一个二阶全极点传递函数。这些二阶函数的乘积得到了 6 阶巴特沃斯传递函数。

极点对

在侧面的图形中，极点 $p_{1}$ 及其复共轭极点距离虚轴很近。它们的幅频响应将在拐角频率处出现过冲。这对应于欠阻尼情况，并且二阶部分将在接近拐角频率的频率处表现出一些共振。

极点 $p_{2}$ 及其复共轭极点相对于虚轴的夹角为 45°。它们的幅频响应将在拐角频率处出现 3 dB 的衰减。这是幅频响应不出现过冲的临界情况。然而，这并不对应于临界阻尼情况：阶跃响应在稳定之前会出现过冲。

极点 $p_{3}$ 及其复共轭极点距离虚轴很远。它们的幅频响应将在拐角频率处出现较大的衰减。这对应于过阻尼情况。

幅频响应

以下 Octave 代码允许绘制各个二阶部分的幅频响应以及全局巴特沃斯幅频响应。

#-------------------------------------------------------------------------------
# Specifications
#
order = 6;
pointNb = 100;
wLog = logspace(-1, 1, pointNb);
AdbMax = 10;
AdbMin = -40;

#-------------------------------------------------------------------------------
# Butterworth filter
#
[num, den] = butter(order, 1, 's');
while ( length(num) < length(den) )
  num = [0, num];
endwhile;

#-------------------------------------------------------------------------------
# Normalized filter, transfer functions plot
#
Adb = 20*log10(abs(freqs(num, den, wLog)));

figure(2);
semilogx(wLog, Adb);
hold on;
for index = 1:order
  if imag(poles(index)) > 0
    num = [0, 0, 1];
    den = [1, -2*real(poles(index)), abs(poles(index))^2];
    Adb = 20*log10(abs(freqs(num, den, wLog)));
    semilogx(wLog, Adb, 'g');
  endif
endfor
hold off;

axis([wLog(1), wLog(length(wLog)), AdbMin, AdbMax]);
xlabel('Frequency');
ylabel('Amplitude responses');
grid;

侧面蓝色曲线显示全局幅频响应。

绿色曲线是各个二阶部分的响应。它们都具有一个水平渐近线趋向于直流。它们也都有一个高频 -40 dB/decade 的渐近线。这两个渐近线在点 ( $\omega =1$ [s^-1], $A=0$ [dB]) 相交。拐角频率位于 $\omega =1$ [s^-1] 或 $f=1/{(2\pi )}$ [Hz]

高 Q 值二阶函数

顶部的绿色幅频响应显示了高品质因数响应的样子。它在略低于拐角频率的频率处有一个超过 0 dB（此处为 6.02 dB）的峰值。在拐角频率处，幅度已经下降（此处为 5.68 dB）。

最大平坦二阶函数

中间的绿色幅频响应显示了最大平坦响应的样子。它在拐角频率处具有 -3.02 dB 的幅度。

无论阶数如何，巴特沃斯函数在拐角频率处都表现出相同的 -3.02 dB 衰减。

低 Q 值二阶函数

底部的绿色幅频响应显示了低品质因数响应的样子。它在拐角频率处具有小于 -3 dB（此处为 -5.72 dB）的幅度。