跳转至内容

传统算盘与珠算/除法/现代除法与传统除法；密切相关的亲属

Add links
来自维基教科书，开放书籍，为开放世界
< 传统算盘与珠算 | 除法
此页面可能需要审查质量。

介绍

[编辑 | 编辑源代码]

如前一章所述，算盘中使用两种主要除法方法：**现代除法**和**传统除法**。现代除法（**MD**），日语为shojohou，中文为shāng chúfǎ（商除法），实际上是最古老的，可以追溯到公元 200 年左右，只使用乘法表。相比之下，传统方法（**TD**），kijohou，guī chúfǎ（帰除法），更晚但也很古老，可以追溯到算筹时代，至少从 13 世纪开始。此方法使用乘法表和特定的除法表。**TD** 至少在过去的 4 个世纪里一直是算盘教学中的标准方法[1][2]，在 20 世纪 30 年代开始失去人气。原因是现代算盘学生在开始学习算盘之前已经知道如何用铅笔和纸计算除法，并且由于学习计划非常紧凑或非常忙碌，他们没有时间学习新的除法方法和记忆新的表格，而是利用现有的知识；**MD** 是算盘上最接近书面长除法的操作。

很难说这两种除法方法哪种更有效，Kojima[3] 不敢说，但普遍认为传统方法更舒适或轻松，因为人们不必思考任何东西，只需遵循规则即可。从以下内容可以看出，**MD** 比**TD** 有效（更快），可以说**MD** 适合短跑运动员，**TD** 适合马拉松运动员；也就是说，对于每天要花费很多时间做除法的人来说……

乍一看，这两种除法方法似乎截然不同，我们将在下文中展示这两种方法是如此相似和相关，以至于它们可以被认为是密切相关的亲属（**MD** 是哥哥，**TD** 是弟弟），以至于如果你已经精通**MD**，那么你也精通**TD**！……尽管你还不了解，而且你离完全掌握**TD** 的力量还很远。

为此，我们将回到更古老的除法方法，以便将**MD** 和**TD** 置于分块方法[4]（有时也称为部分商方法或刽子手方法）的框架内，这将使我们能够展示两种方法的极端相似之处。之后，我们将深入探讨 TD 的隐藏美，并了解为什么它简化了算盘的操作。在下文中，我们假设你已经了解算盘上的现代除法，如何上下修改等，例如，Kojima 的解释。

最初的方法

[编辑 | 编辑源代码]

以 1225÷35 = 35 为例。最简单的方法是重复减法，因为 35 大于被除数的前两位数字，我们将从 122 中减去 35，使用算盘上的一个列作为计数器。

1225÷35 = 35
算盘 注释
ABCDEFGHI
35   1225 开始，计数器在 D 中，
35 1  875 从 GH 中减去 35，将计数器 D 加 1，
35 2  525 从 GH 中减去 35，将计数器 D 加 1，
35 3  175 从 GH 中减去 35，将计数器 D 加 1，
35 31 140 从 HI 中减去 35，将计数器 E 加 1，
35 32 105 从 HI 中减去 35，将计数器 E 加 1，
35 33  70 从 HI 中减去 35，将计数器 E 加 1，
35 34  35 从 HI 中减去 35，将计数器 E 加 1，
35 35  00 从 HI 中减去 35，将计数器 E 加 1。
35 35 没有余数。完成，商是 35！

这很简单，但有点长。如果我们可以轻松地将除数加倍并将其保存在内存中，我们可以通过减去除数块的一两倍来缩短操作。

倍数 块
1 35
2 70
1225÷35 = 35
算盘 注释
ABCDEFGHI
35   1225 开始，计数器在 D 中，
35 2  525 从 GH 中减去 70，将计数器 D 加 2，
35 3  175 从 GH 中减去 35，将计数器 D 加 1，
35 32 105 从 HI 中减去 70，将计数器 E 加 2，
35 34  35 从 HI 中减去 70，将计数器 E 加 2，
35 35  00 从 HI 中减去 35，将计数器 E 加 1。
35 35 没有余数。完成，商是 35！


或者更好的是，如果我们可以像下面这样通过将除数加倍三次来建立一个表格[5]

倍数 块
1 35
2 70
4 140
8 280
1225÷35 = 35
算盘 注释
ABCDEFGHI
35   1225 开始，计数器在 D 中，
35 2  525 从 GH 中减去 70，将计数器 D 加 2，
35 3  175 从 GH 中减去 35，将计数器 D 加 1，
35 34  35 从 HI 中减去 140，将计数器 E 加 4，
35 35   0 从 HI 中减去 35，将计数器 E 加 1。
35 35 没有余数。完成，商是 35！

这稍微短一些，而且很明显，没有什么比拥有除数的完整乘法表更快了

35 的乘法表
倍数 块
1 35
2 70
3 105
4 140
5 175
6 210
7 245
8 280
9 315

然后

1225÷35 = 35
算盘 注释
ABCDEFGHI
35   1225 开始，计数器在 D 中，
35 3  175 从 GH 中减去 105，将计数器 D 加 3，
35 35  00 从 HI 中减去 175，将计数器 E 加 5。
35 35 没有余数。完成，商是 35！

毫无疑问，这是一种最佳的除法方法，一旦我们有了像上面这样的块表，就没有任何东西能更快、更舒适了……但是计算块表非常耗时，需要纸笔来写，只有当我们要对同一个除数进行大量除法时，这种额外的工作才合理。

1617 年，约翰·纳皮尔，对数之父，展示了他的发明来解决这个问题，发明了一系列称为纳皮尔的骨头的杆，上面写着一位数的乘法表，可以组合起来得到任何数字的乘法表。例如，在我们的例子中

中国一套纳皮尔骨头
使用纳皮尔骨头的 35 乘法表
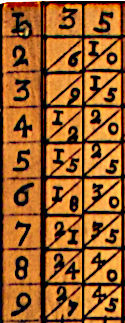
Napier's bones multiply by 35 1 35
2 70
3 105
4 140
5 175
6 210
7 245
8 280
9 315

毫无疑问，这样的发明传播到东方，并与算盘一起使用，但这种使用必须被认为是例外；并非每个人都随身携带纳皮尔骨头。需要另一种工具，那就是死记硬背的乘法表。

应该注意的是，以上过程并没有穷尽分块方法的所有可能性。如果你阅读了关于整数长除法的决定性高等数学指南[4] 文章，你将对可以执行的各种除法方法感到惊讶。算盘中使用的**MD** 和**TD** 都属于这一类，正如我们将要看到的。

现代除法（商除法）

[编辑 | 编辑源代码]

学习算盘的一个关键点是意识到这种工具使我们能够非常快速地纠正一些错误，而且不会留下痕迹，这在除法中特别有用。因此，如果我们要计算 634263÷79283，与其费尽心思地试图找到正确的商位，不如简单地通过将原始问题简化为 63÷7 来选择一个近似的临时或中间数字，然后尝试从被除数中减去块（中间商位）✕79283；将出现以下情况之一

  • 中间商位是正确的
  • 它过大，我们必须将其向下修改
  • 它不足，我们必须将其向上修改

让我们看看它应用于我们之前的示例。与其直接尝试解决 1225÷35，不如简化并尝试使用记忆中的 3 的乘法表解决 12÷3。

3×1 3
3×2 6
3×3 9
3×4 12
3×5 15
3×6 18
3×7 21
3×8 24
3×9 27
1225÷35 = 35
算盘 注释
ABCDEFGHI
35   1225 12÷3↦4，从上面的表格中得到 3×4=12
   +4 将中间商位输入 E
35  41225 现在尝试从 FGH 中减去块 4✕35，
    -12 首先从 FG 中减去 4✕3
35  40025 然后从 GH 中减去 4✕5
     -20 无法减去！
   -1 向下修改中间商位
35  30025
     +3 将从 FG 中减去的超额部分归还
35  30325
     -15 继续正常操作，从 GH 中减去 3✕5
35  3 175 17÷3↦5，从上面的表格中得到 3×5=15
    +5 将中间商位输入 F
35  35175 尝试从 GHI 中减去块 5✕35
     -15 首先从 GH 中减去 5✕3
35  35025
      -25 然后从 HI 中减去 5✕5
35  35 没有余数，完成！1225÷35 = 35

传统除法（帰除法）

[编辑 | 编辑源代码]

我们不直接尝试解决原始问题 1225 ÷ 35 或在 MD 中使用的近似值 12 ÷ 3，而是进一步简化，尝试解决 10 ÷ 3；也就是说，我们通过忽略被除数的第二位数字，对原始问题采用更粗略的方法，因此我们必须准备更频繁地修改中间商。通过将关注点从 12 ÷ 3 变为 10 ÷ 3，我们采用了 TD 的理念；它只是 MD 中使用的分块技术的微小变化。这就是为什么我们可以将两种除法机制视为近亲，它们都是分块算法家族的成员……这也说明了，如果你已经精通现代除法，那么你已经精通传统除法！但让我们继续...

继续我们的例子

1225 ÷ 35
算盘 注释
ABCDEFGHI
35   1225 10 ÷ 3 ↦ 3 来自乘法表
   +3 将中间商位输入 E
35  31225 尝试从 FGH 中减去块 3 × 35，
    -09 首先 3 × 3 从 FG 中减去
35  3 325
     -15 然后 3 × 5 从 GH 中减去
35  3 175 好的。
35  3 175 10 ÷ 3 ↦ 3
    +3 将中间商位输入 F
35  33175 尝试从 GHI 中减去 3 × 35，
     -09 首先 3 × 3 从 GH 中减去
35  33 85
      -15 然后 3 × 5 从 HI 中减去
35  33 70 余数大于除数 (35)
    +1-35 向上修正
35  34 35 余数等于除数 (35)
    +1-35 再次向上修正
35  35 没有余数，完成！1225÷35 = 35


请注意，正如我们迄今为止所解释的，MD 和 TD 可以在同一个除法问题中自由混合。这是一个有趣的推荐练习，可以让你将两种策略并排比较。

TS 比 MD 对原始问题采用了更简单、更低级的处理方法，因此我们可以预见到一些优缺点。

  • 优点
    • 有些人可能会认为这种方法更简单
    • 向下修正的频率会更低（向下修正通常比向上修正更困难，更容易出错）
  • 缺点
    • 我们需要更频繁地修改中间商，这是一个效率问题。

以上提到的两个优点可能在传统除法这种复杂技术的演变过程中发挥了作用，但要理解为什么它在几个世纪以来仍然是首选方法，尽管存在上述缺点，我们需要思考除法过程中所做的智力努力的起源，并发现 TD 中隐藏的美丽。

智力努力的来源

[edit | edit source]

当我们学习乘法表时，我们记住了诸如以下的短语序列：

“九九八十一”
“九八七十二”
...


学习这些短语的顺序可能有所不同，但短语的结构在所有语言中都是相似的，至少在汉语和日语中是这样的。它包含一个包含要相乘的两个因子的标签，后面跟着积。只要我们想到标签，它就像一个咒语，将积的值召唤到我们的意识中。让我们用以下方式表示它（将 ➡ 视为调用）

语言 标签 产品
英语 九乘九 ➡ 八十一
中文 九九 ➡ 八十一
日语 くく ➡ はちじゅういち
符号 9 × 9 ➡ 81

我们在除法过程中如何使用乘法表？让我们考虑一下上面的例子，使用商除法或现代除法方法：17 ÷ 3 ↦ 5，从三的乘法表中，我们需要找到可以从 17 中减去的最大积。我们需要在我们的记忆中扫描（用 ⤷ 表示）至少该表中的几行，对于每个找到的积，看看它是否小于 17，并选择那些小于 17 的最大积。这是一个复杂的过程，可以用以下方式表示：

3 × 1 ➡ 3
3 × 2 ➡ 6
⤷ 3 × 3 ➡ 9 是
⤷ 3 × 4 ➡ 12 是
⤷ 3 × 5 ➡ 15 是 选择这个！
⤷ 3 × 6 ➡ 18 否
3 × 7 ➡ 21
3 × 8 ➡ 24
3 × 9 ➡ 27

这个过程耗时费力。计算机专家可能会发现这个过程与在非索引列上搜索关系数据库表类似；这种搜索的低效率是众所周知的。根据列和搜索条件创建新的索引或键可以极大地改善情况。我们能否在我们的案例中做一些类似的事情，使除法更舒适？

索引乘法表（除法表）

[edit | edit source]

为了做一些类似于索引乘法表以方便搜索积的事情，我们应该记住新的短语，这些短语包含这些积作为标签；也就是说，以这些积开头的短语；例如

标签 商
3/3 1
6/3 2
9/3 3
12/3 4
15/3 5
18/3 6
21/3 7
24/3 8
27/3 9

也就是说，我们必须记住一个除法表，这是一个艰苦的工作。此外，请注意，上面的表格并不是最优的，因为 1 到 29 之间的大多数数字都缺失了；也许我们应该记住一个以下风格的表格：

标签 商 余数
1/3 0 1
2/3 0 2
3/3 1 0
4/3 1 1
5/3 1 2
… … …
27/3 9 0
28/3 9 1
29/3 9 2

其中第三列包含欧几里得除法的余数。你可能会同意，记忆这样一个表格是普通人无法做到的（想想 9 的表格！）。

传统除法的隐藏美丽

[edit | edit source]

如果我们花一生的时间使用 MD 方法用算盘进行除法，我们最终将面临所有类型为 ab ÷ c 的基本除法，其中 a、b 和 c 是数字，并且 ab < c0，总共大约 360 个。然而，如果我们使用 TD，我们将面临所有类型为 a0 ÷ c 或 (10 × a) ÷ c 的基本除法，总共只有 36 个！... 这使得记忆除法表变得可行。事实上，要除以 3，只需要记住

标签 商 余数
10/3 3 1
20/3 6 2

或者，以更简洁的符号形式

规则
1/3 > 3+1
2/3 > 6+2

我们可以直接使用这个规则来解决我们的示例，而无需任何思考，只需简单地选择规则建议的数字作为中间商。

1225÷35 = 35
算盘 注释
ABCDEFGHI
35   1225 使用规则 1/3 > 3 + 1
   +3 将中间商位输入 E
35  31225 尝试从 FGH 中减去块 3 × 35，
    -09 首先 3 × 3 从 FG 中减去
35  3 325
     -15 然后 3 × 5 从 GH 中减去
35  3 175 好的。
35  3 175 使用规则 1/3 > 3 + 1
    +3 将中间商位输入 F
35  33175 尝试从 GHI 中减去 3 × 35，
     -09 首先 3 × 3 从 GH 中减去
35  33 85
      -15 然后 3 × 5 从 HI 中减去
35  33 70 余数大于除数 (35)
    +1-35 向上修正
35  34 35 余数等于除数 (35)
    +1-35 再次向上修正
35  35 没有余数，完成！1225÷35 = 35

但我们还没有利用规则中加号后面的余数；这个以及其他问题将在下一章中介绍。

除法表

[edit | edit source]

最后，我们提供 TD 中使用的完整除法表。所有元素都通过 a0 ÷ c 项的欧几里得除法获得。

除法表 (八算, Hassan, Bā suàn)
1/9>1+1 2/9>2+2 3/9>3+3 4/9>4+4 5/9>5+5 6/9>6+6 7/9>7+7 8/9>8+8 9/9>9+9
1/8>1+2 2/8>2+4 3/8>3+6 4/8>5+0 5/8>6+2 6/8>7+4 7/8>8+6 8/8>9+8
1/7>1+3 2/7>2+6 3/7>4+2 4/7>5+5 5/7>7+1 6/7>8+4 7/7>9+7
1/6>1+4 2/6>3+2 3/6>5+0 4/6>6+4 5/6>8+2 6/6>9+6
1/5>2+0 2/5>4+0 3/5>6+0 4/5>8+0 5/5>9+5
1/4>2+2 2/4>5+0 3/4>7+2 4/4>9+4
1/3>3+1 2/3>6+2 3/3>9+3
1/2>5+0 2/2>9+2
1/1>9+1

参考资料

[edit | edit source]
  1. ↑ Xú Xīnlǔ (徐心魯) (1993) [1573]. Pánzhū Suànfǎ (盤珠算法) (in Chinese). Zhōngguó kēxué jìshù diǎnjí tōng huì (中國科學技術典籍通彙). {{cite book}}: Unknown parameter |trans_title= ignored (|trans-title= suggested) (help)
  2. ↑ 篠田正作 (1895). 実用算術 (Jitsuyo Sanjutsu) (日语). {{cite book}}: 未知参数 |trans_title= 被忽略（建议使用 |trans-title=) (帮助)
  3. ↑ Kojima, Takashi (1954), The Japanese Abacus: its Use and Theory, 东京: Charles E. Tuttle Co., Inc., ISBN 978-0-8048-0278-9
  4. ↑ a b "The Definitive Higher Math Guide on Integer Long Division (and Its Variants)". Math Vault. 存档于 原始 于 2021年5月14日. {{cite web}}: 未知参数 |accesdate= 被忽略（建议使用 |access-date=) (帮助); 未知参数 |name= 被忽略 (帮助)
  5. ↑ Wilson, Jeff. "Long Division Teaching Aid, "Double Division"". Double Division. 存档于 原始 于 2021年3月2日. {{cite web}}: 检查 |archivedate= 中的日期值 (帮助); 文本 "year 2005" 被忽略 (帮助); 未知参数 |accesdate= 被忽略（建议使用 |access-date=) (帮助)

进一步阅读

[编辑 | 编辑源代码]


下一页: 归除法指南 (Guide to traditional division (帰除法)) | 上一页: 除法 (Division)
主页: 传统算盘珠算/除法 (Traditional Abacus and Bead Arithmetic/Division)
取自 "https://wikibooks.cn/wiki/Traditional_Abacus_and_Bead_Arithmetic/Division/Modern_and_traditional_division;_close_relatives"
华夏公益教科书