传统算盘与珠算/简介

前言

东方算盘（简体中文：算盘；繁体中文：算盤；拼音：suànpán，日语： そろばん soroban，在本教科书中简称为算盘），作为一种固定珠子在算珠上滑动的算盘，起源于中国，具体日期尚不清楚，但到16世纪后期，算盘的使用完全取代了算筹，成为其母国的一种计算工具。从中国，算盘的使用传播到其他邻国，特别是日本、韩国和越南，一直是主要的计算工具，直到现代。算盘的使用方法，“传统方法”，至少保持了四个世纪的稳定，直到19世纪末，才开始向我们所说的“现代方法”演变，这种方法使用“现代算盘”。本教科书旨在介绍传统方法，目标读者是那些已经知道如何使用现代算盘进行现代方法计算的人。

现代算盘与传统算盘

现代4+1算盘

5+3 和 5+1 算盘

现代算盘是4+1型的，也就是说它在下层有四个算珠，在上层有一个算珠。

4+1 算盘数字表示

	0	1	2	3	4	5	6	7	8	9

这正是能够用算盘进行十进制运算所需要的全部。然而，传统的算盘有额外的算珠，最常见的是5+2型（尽管5+1型在日本也很流行），偶尔也有5+3型。

传统5+2 中国算盘，展示了悬珠的使用

用三个上层算珠，我们可以在一根算珠上存储最多20个数字，这对于传统的除法和乘法技术来说很方便。用两个上层算珠，我们可以通过使用悬珠技术（悬珠，中文：Xuán zhū，日语：kenshu）来实现同样的效果，这是一种模拟或虚拟的上层第三个算珠，在需要用到第三个算珠的罕见情况下使用（见图15到20）。

5+2 算盘数字表示

	0	1	2	3	4	5	5	6	7	8	9	10

	10	11	12	13	14	15	15	16	17	18	19	20

用一个下层第五个算珠，我们有两种不同的方法来表示数字5、10和15。这意味着我们可以选择最方便的方法。在加法和减法的情况下，能够在5和10的两种表示方法之间进行选择，将允许我们简化一些计算。

传统技术可以应用于任何类型的算盘，只是在4+1算盘上使用下层第五个算珠这一点例外，有没有额外的上层算珠的区别更多的是舒适度和可靠性问题，而不是效率或能力问题。

现代方法与传统方法

传统方法至少使用了四个世纪，涵盖了中国的明朝和清朝，以及日本的江户时代。从日本的明治维新开始，学习算盘的学生在学习算盘之前就已经掌握了书面数学，而早期的学生之前对数学一无所知。对于大多数人来说，算盘是他们唯一会学习的数学形式。这就导致了算盘的教学和方法随着时代和环境的变化而缓慢地适应，在几十年的时间里，逐渐形成了我们现在所说的现代方法，事实上，它是一种简化的方法。

在英语中，下面两部由高岛隆志（Takashi Kojima）撰写的著作经常被引用，用来参考现代方法

• 《日本算盘：使用方法和理论》（1954）
• 《高级算盘：理论与实践》（1963）

这两本书的几个版本仍然可以找到，包括电子书格式，第一本书可以在archive.org上查阅。在本维基教科书中，假定读者熟悉这两本书至少第一本的内容。

今天，现代方法在很多方面似乎是最优的，我们可能会认为传统方法中的一些“怪异之处”，特别是算盘上除法的组织方式，缺乏实际意义；但如果传统方法在几个世纪的时间里，尽管有数百万用户，包括像关孝和这样的人物，他大力推广了日本使用算盘，它仍然保持稳定，那么一定是因为它的用户也认为它是最优的。只是古人的最优标准与我们今天的标准不同。

不幸的是，过去没有人费心去写为什么事情是这样做的，他们只写了如何去做，我们只能推测这些古老技术背后的原因。

传统方法与现代方法的主要区别

以下三点是传统技术与现代技术最主要的区别

• 在加法和减法中使用下层第五个算珠，可以略微简化这两个操作，这扩展到可以用算盘做的一切，因为所有东西最终都依赖于加法和减法。
• 使用除法表进行除法，消除了确定商位所需的脑力劳动。这种方法（kijohou，guīchúfǎ 归除法）首先由朱世杰（1299）在其《算学启蒙》中使用算筹进行了描述，取代了旧的基于乘法表的除法方法，该方法的起源可以追溯到公元3到5世纪，即《孙子算经》。这种旧方法，作为书面除法短除法和长除法的基础，在现代已经取代了传统的除法方法。也就是说，现代社会又回到了旧方法！
• 传统方法和现代方法在算盘上组织除法的方式上也存在差异。传统的除法排列方式比现代的排列方式更加紧凑，但也更加麻烦，因为它需要（或受益于）使用额外的、更高的算珠。这种除法排列方式反过来影响了乘法和开根号的组织方式。

最小努力原则

如上所述，过去的作者都没有写过为什么事情是这样做的，只写了如何去做；所以我们只能猜测，试图理解背后的原因。但读者将在本书中看到，与现代技术相比，传统技术假设减少了使用算盘所需的脑力劳动。这一点在使用除法表的除法中尤为明显，在其他将要介绍的技术中也体现出来，因为这些技术有效地减少了完成一项操作所需的“手势”的数量和/或范围。我们在这里所说的手势是指

• 手指或算珠的动作
• 手部的移动
• 方向的改变
• 跳跃算珠（即，从一个起始算珠改变手部位置到其他非相邻的算珠）

而每一个手势，

• 作为一个物理过程，需要时间来完成，
• 由我们的大脑控制，需要我们的注意力，消耗（精神或生化）能量，
• 由人类（而不是机器）完成，有做错的可能性，从而导致错误。

因此，我们可以预期，通过减少这些手势的数量和范围，能够实现更快的、更轻松的、更可靠的计算。

鉴于上述情况，人们可能会认为，通过采用这种最小努力原则，传统技术在使算盘生活更轻松的意义上得到了发展，这可以解释其几个世纪以来的有效性，但这仅仅是一种没有文献支持的推测。

如果我们想到现代方法，它倾向于简单、速度和效率，我们可以说它是“短跑者方法”，而传统方法是“马拉松跑者方法”。

读者在阅读完本教材后，将能够得出自己的结论。

算盘操作表、一些术语和符号

像往常一样，在本书中，我们将使用表格来描述算盘上的操作，例如

算盘操作表的示例

算盘	注释
ABCDEFGHIJKLM
896 412	这次除数在左边，被除数在右边
896 512	E 列：规则 4/8>5+0，将 E 中的 4 更改为 5，将 0 添加到 F
896 512	无法从 FG 中减去 E×B=5×9=45，
-1	向下修改 E：从 E 中减去 1，
+8	将 8 添加到 F
896 492
等等。	等等。

左边显示了算盘状态的逐位演变，或者显示了当前的加减运算，以及相关注释；右边显示了正在执行的操作。算盘的列在顶部用字母标记（空白空间表示未使用的/清除的算珠）。

这种表示方法对于现代算盘来说是完美的，但需要进行一些调整以适应传统算盘。

• 传统算盘的一列可以包含大于 9 的数字，并且无法在表格中写入其两位数字而不会破坏其垂直对齐。为了解决这个问题，我们将对 10 到 19 之间的数字使用“下划线符号”，第一个数字（1）将用前一列的下划线表示（请参阅章节 处理溢出 获取原因）。例如，下面显示的情况出现在 998001 除以 999 的传统除法开始不久后

	A	B	C	D	E	F	G	H	I	K	J	L	M
	9	18	9	0	0	1	0	0	0	0	9	9	9

在操作表中表示为

使用下划线符号

算盘	注释
ABCDEFGHIJKLM
988001    999	B 列的值为 18

• 

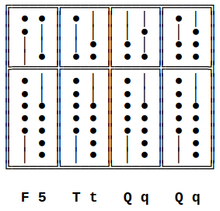
  与使用第五个下珠相关的符号

  如上所示，数字 5、10 和 15 有两种可能的表示形式：使用或不使用第五个下珠。当需要区分这两种情况时，我们将使用以下代码
  • F： 表示“下五”（激活五个下珠），与
  • 5： “上五”（激活一个上珠）相反。
  • T： 一列上的十（激活一个上珠和五个下珠）。在 5+2 型算盘上，它也是“下十”，与“上十”（激活两个上珠）相反。
  • Q： 一列上的“下十五”（激活两个上珠和五个下珠），与“上十五”（5+2 型算盘上的悬挂上珠，5+3 型算盘上的三个上珠）相反。

外部资源

算盘训练器

算盘训练器展示了一个使用悬挂上珠的 5+2 型算盘。

如果您对传统技术感兴趣，但还没有传统算盘，可以使用 JavaScript 应用程序

 Soroban Trainer 

• 您可以在浏览器中 直接从 GitHub 运行它
• 或者您可以从 GitHub 上的仓库 下载到您的计算机上。