三角函数/余弦加法公式

余弦公式

我们证明了正弦加法公式；现在我们将证明余弦加法公式。

$\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

在进行证明之前，我们将讨论减法公式。

减法公式 您无需学习或记忆正弦和余弦的特殊减法公式或“角差”公式。您可以使用正弦和余弦加法公式“立即”计算出它们，使用 $\sin(-x)=-\sin(x)$ 和 $\cos(-x)=\cos(x)$ 。 让我们将 $\displaystyle (-\beta )$ 代替 $\displaystyle \beta$ 代入两个加法公式 首先是正弦加法公式 $\sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )$ 变为 $\sin {\big (}\alpha +(-\beta ){\big )}=\sin(\alpha )\cos(-\beta )+\cos(\alpha )\sin(-\beta )$ $\sin(\alpha -\beta )=\sin(\alpha )\cos(\beta )-\cos(\alpha )\sin(\beta )$ 现在是余弦加法公式 $\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$ 变为 $\cos {\big (}\alpha +(-\beta ){\big )}=\cos(\alpha )\cos(-\beta )-\sin(\alpha )\sin(-\beta )$ $\cos(\alpha -\beta )=\cos(\alpha )\cos(\beta )+\sin(\alpha )\sin(\beta )$ 将四个公式结合起来 如果我们真的想的话，可以将四个加法和“角差”公式用更简洁的记号写成 $\cos(\alpha \pm \beta )=\cos(\alpha )\cos(\beta )\mp \sin(\alpha )\sin(\beta )$ $\sin(\alpha \pm \beta )=\sin(\alpha )\cos(\beta )\pm \cos(\alpha )\sin(\beta )$ 如果你喜欢这种风格，就用它吧。我们建议你还是先学习加法公式，当你需要差值公式时，再从加法公式推导出来。

现在要证明

$\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

如约所说。

证明

视频链接

有很多关于证明的视频

• 证明：$\cos(a+b)=\cos(a)\cos(b)-\sin(a)\sin(b)$

证明过程

我们需要证明

$\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

我们将使用上一页练习中使用的技巧，设置 $AB=1$，并使用与上次完全相同的图形。

由于$\triangle ABE$ 是一个直角三角形，斜边长度为 1，角 $\beta$，因此我们有

${\overline {BE}}=\sin(\beta )$

${\overline {AE}}=\cos(\beta )$

同样，因为$\triangle ABC$ 是一个直角三角形，斜边长度为 1，角 $(\alpha +\beta )$，因此我们有

${\overline {AC}}=\cos(\alpha +\beta )$

让我们用角度的余弦和正弦来表示${\overline {AF}}$ 和 ${\overline {DE}}$。你需要查看图表以了解我们正在使用哪些三角形。

对于${\overline {AF}}$ 的表达式 ${\overline {AF}}={\overline {AE}}\cos(\alpha )$ 所以 ${\overline {AF}}=\cos(\alpha )\cos(\beta )$

对于${\overline {DE}}$ 的表达式 ${\overline {DE}}={\overline {BE}}\sin(\alpha )$ 所以 ${\overline {DE}}=\sin(\alpha )\sin(\beta )$

$\cos(\alpha +\beta )={\overline {AC}}={\overline {AF}}-{\overline {CF}}={\overline {AF}}-{\overline {DE}}$

$\cos(\alpha +\beta )=\cos(\beta )\cos(\alpha )-\sin(\beta )\sin(\alpha )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$

完成！

另一种方法

这个证明看起来非常类似于 $\sin(\alpha +\beta )$

实例：从正弦加法公式推导出余弦加法公式

从

$\sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )$

我们使用 $\sin(x)=\cos(90^{\circ }-x)$ 和 $\cos(x)=\sin(90^{\circ }-x)$ （并在多个地方进行替换）

$\cos {\big (}90^{\circ }-(\alpha +\beta ){\big )}=\cos(90^{\circ }-\alpha )\cos(\beta )+\sin(90^{\circ }-\alpha )\sin(\beta )$

现在我们使用 $\cos(-x)=\cos(x)$ 和 $\sin(-x)=-\sin(x)$

$\cos {\big (}-(90^{\circ }-(\alpha +\beta )){\big )}=\cos {\big (}-(90^{\circ }-\alpha ){\big )}\cos(\beta )-\sin {\big (}-(90^{\circ }-\alpha ){\big )}\sin(\beta )$

$\cos(\alpha +\beta -90^{\circ })=\cos(\alpha -90^{\circ })\cos(\beta )-\sin(\alpha -90)\sin(\beta )$

这对所有$\alpha ,\beta$都成立，所以如果我们令$\alpha =A+90^{\circ }$和$\beta =B$，我们得到

$\cos(A+B)=\cos(A)\cos(B)-\sin(A)\sin(B)$

现在轮到您练习从旧公式中推导出新公式了

练习：从余弦加法公式推导出正弦加法公式 从 $\cos(\alpha +\beta )=\cos(\alpha )\cos(\beta )-\sin(\alpha )\sin(\beta )$ 证明 $\sin(\alpha +\beta )=\sin(\alpha )\cos(\beta )+\cos(\alpha )\sin(\beta )$

一个更难的练习

练习：正切加法公式 使用 $\tan(x)={\frac {\sin(x)}{\cos(x)}}$ 以及正弦和余弦的加法公式，证明 $\tan(A+B)={\frac {\tan(A)+\tan(B)}{1-\tan(A)\tan(B)}}$

现在轮到您进行加法公式的几何证明了。

练习：使用不同的图表进行证明 您可能想跳过此练习，并在使用余弦加法公式一段时间后再来做。这是让您自信地自己编写公式的几何证明的一个很好的练习。 从下图开始 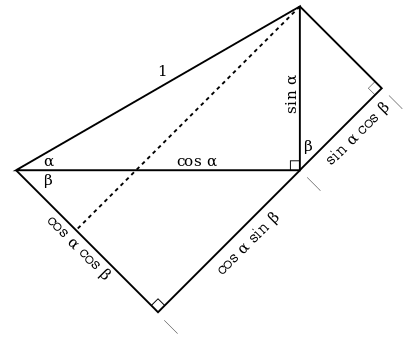添加标签，并写出证明 正弦加法公式 余弦加法公式 基于图表和您选择的字母。确保您通过追溯角度来解释为什么标有$\beta$的两个角度是相同的。给边缘长度的标签是为了帮助您。您的证明必须使用三角关系来解释为什么这些标签是正确的。 比较上面的证明中的图表。它们真的有多不同？