三角学/给爱好者/李萨如图形

李萨如曲线

在示波器上的李萨如图形

一个李萨如曲线是以下方程的图形

$x=A\sin(at+\delta ),\quad y=B\sin(bt),$

其中$\displaystyle a,b,A,B$ 和 $\displaystyle \delta$ 是选定的值，并且 $\displaystyle t$ 变化。

a = 5, b = 4 (5:4)

这是我们在练习绘制 cos t vs sin t中绘制的圆的图形的推广。

事实上，如果我们设置

$\displaystyle a=1,b=1,A=1,B=1$ 以及 $\displaystyle \delta =\pi /2$

在李萨如曲线方程中，就可以得到圆。

检查一下 不要只相信我们的说法，李萨如方程是圆方程的推广。将这些值代入方程并化简。利用你所知道的正弦和余弦之间的关系。然后回答以下问题 随着 $\displaystyle t$ 增加，以及这些$\displaystyle a,b,A,B$ 和 $\displaystyle \delta$ 的值，绘制的点是沿圆的相同方向还是与之前“单位圆”练习中的相反方向移动？

这组曲线由纳撒尼尔·鲍迪奇在 1815 年研究，后来由朱尔斯·安托万·李萨如在 1857 年更详细地研究。

例子

以下是李萨如图形的例子，所有图形的 δ = 0。

• 
  a = 1, b = 2 (1:2)
• 
  a = 3, b = 2 (3:2)
• 
  a = 3, b = 4 (3:4)
• 
  a = 5, b = 4 (5:4)
• 
  a = 5, b = 6 (5:6)
• 
  a = 9, b = 8 (9:8)

图形的外观对比率 a/b 非常敏感。对于比率为 1 的情况，图形是椭圆，特殊情况包括圆 (A = B, δ = π/2 弧度) 和直线 (δ = 0)。另一个简单的李萨如图形是抛物线 (a/b = 2, δ = π/2)。如果 δ = 0，曲线必须通过原点，因为在这种情况下，当 t = 0 时，x 和 y 都为 0。对于相同的 a/b 值，但不同的 δ 值，可能会出现截然不同的曲线。

检查一下 自己尝试一下直线。 你能使直线垂直吗？

其他比率会产生更复杂的曲线，只有当 a/b 是有理数时，这些曲线才是封闭的。这些曲线的视觉形式通常让人想起三维结，实际上，许多种结，包括被称为李萨如结的结，投影到平面上的就是李萨如图形。

对于 a = 1, b = N (N 是自然数) 和

$\delta ={\frac {N-1}{N}}{\frac {\pi }{2}}\$

的李萨如图形是切比雪夫多项式的第一类，其次数为 N。

生成

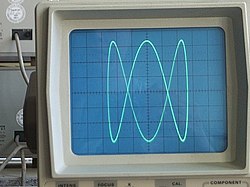
在现代计算机图形出现之前，李萨如曲线通常是用示波器生成的（如插图所示）。将两个相位移位的正弦波输入信号应用于示波器，在 X-Y 模式下，信号之间的相位关系将以李萨如图形的形式呈现。

在示波器上，我们假设 x 是 CH1，y 是 CH2，A 是 CH1 的幅度，B 是 CH2 的幅度，a 是 CH1 的频率，b 是 CH2 的频率，因此 a/b 是两个通道频率的比率，最后，δ 是 CH1 的相位移。

当 a = b 时的应用

当输入到LTI 系统的是正弦波时，输出将是具有相同频率的正弦波，但幅度可能不同，并且存在相移。使用可以绘制一个信号相对于另一个信号（而不是一个信号相对于时间）的示波器来绘制 LTI 系统的输出相对于 LTI 系统的输入，将产生一个椭圆，该椭圆是在特殊情况下a = b 的利萨如图形。所得椭圆的偏心率是输入和输出之间相移的函数，偏心率为 1 对应于相移为 $\pm 90^{\circ }$，偏心率为 $\infty$ 对应于 0 或 180 度的相移。下图总结了利萨如图形如何在不同的相移下变化。箭头显示利萨如图形的旋转方向。

纯相移会影响利萨如椭圆的偏心率。分析椭圆可以测量来自LTI 系统的相移。

利萨如图形最早由纳撒尼尔·鲍迪奇在 1815 年提到，并由朱尔斯·安托万·利萨如在 1857 年重新发现。如果周期相等，曲线始终是椭圆。如果一个周期是另一个周期的两倍，我们将得到一条四次曲线；一个特例是伯努利双纽线。