三角学/正弦平方图

正弦平方

下图显示了$(\sin(x))^{2}$ 或 $\sin ^{2}(x)$ 的图形，如通常所写。

这个函数

• 必须是非负的，因为负数的平方总是正的。
• 不能超过 1，因为 $\sin(x)$ 始终介于 -1 和 1 之间。

它看起来像一个平移压缩过的正弦或余弦波。它确实是。当我们查看二倍角公式并证明 $\sin ^{2}(x)={\frac {1-\cos(2x)}{2}}$ 时，我们将证明这一点。

练习：点检 图形正确吗？尝试一些实际值，看看它们是否被绘制在正确的位置。 在该图形中，任何$\sin(x)=0$ 的值也将为零。 在该图形中，任何$\sin(x)=\pm 1$ 的值将为 1。 在该图形上具有$y=0.5$ 的值呢？哪些$\sin(x)$ 值有效？

幅度、频率和相位 从$\sin(x)$ 到$\sin ^{2}(x)$ 幅度减半。（y 值介于 0 和 +1 之间，之前介于 -1 和 +1 之间）。 频率加倍。（在相同的 x 距离内有更多完整的循环）。 相位...好吧，我们可以说相位发生了变化，但只有比较两个相同频率的波的相位才有意义，因此很难说相位发生了什么变化。

余弦平方

下图对 $\cos ^{2}(x)$ 进行了同样的操作。

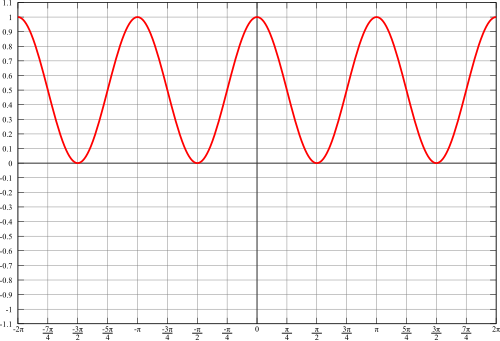
同样，这个函数

• 必须是非负的，因为负数的平方总是正的。
• 不能超过 1，因为 $\cos(x)$ 始终介于 -1 和 1 之间。

比较这两个图形，它们看起来会加起来为 1。它们确实如此。这是一种图形方式来展示我们之前已经看到的内容，即

$\cos ^{2}(x)+\sin ^{2}(x)=1$

余弦平方公式 利用我们已经证明的结论 $\cos ^{2}(x)+\sin ^{2}(x)=1$ 并假设稍后我们将证明的结果 $\sin ^{2}(x)={\frac {1-\cos(2x)}{2}}$ 求解表达式 $\cos ^{2}(x)=$ 注意符号和括号，因为你正在对一个负数取负数。确保简化公式 - 你的答案应该至少与$\sin ^{2}(x)$公式一样简单。 你得出的公式看起来与我们为$\cos ^{2}(x)$绘制的图形一致吗？