三角学/入门
三角学是研究三角形性质的学科。
- "Tri" 是古希腊语中的三个,
- "gon" 意思是角,
- "metry" 测量
合起来就是 "测量三角形的三个角"。
如果你知道一个三角形的一些信息,例如它的边长,那么使用三角学,你就可以找到关于它的其他信息。如果你知道边长,那么你可以找到角度。如果你知道一边的长度和两个角,那么你就可以计算出剩下的角,以及另外两边的长度。
因此,古希腊人能够利用三角学来计算地球到月球的距离。
我们学习三角学的第一件事就是如何在给定另外两个角的情况下计算三角形的第三个角。例如,在一个三角形中,如果两个角是 ,那么第三个角也必须是 ,因为我们知道它们必须加起来等于 。
但是,如果我们被告知两个边长,比如 7cm 和 10cm,并且没有被告知任何关于角的信息,那么第三个边长就有一系列的可能性,它可以在 0 到 17cm 之间。
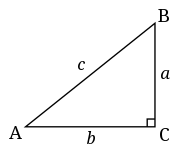
记住,一个直角三角形有一个角是 (一个 "直角")。计算直角三角形上缺失的第三个角要简单得多,所以我们将从考察一个直角三角形开始,预计在本书的其余部分会看到更多这样的三角形。
在直角三角形中,如果给出两个较短边的长度,我们可以计算出最长边的长度。在直角三角形中,边长之间有特别好的关系。这种关系的公式写成
边 和 是与 角相邻的边,而 是与之相对的较长的对角线。你可能有时会看到 被称为斜边。
参见 勾股定理,开始使用此公式来计算缺失边长的长度。
但是,如果三角形不是直角三角形呢?
更复杂的三角形可以很容易地分成直角三角形,因此我们学习直角三角形使我们能够处理其他类型的三角形。三角学和三角函数也可以用于更复杂的形状,例如正方形、六边形、圆形和椭圆形。最终,我们用来测量宇宙的最重要的数学工具是基于对三角形数学的研究。
三角学是你的数学教育中的一个基本步骤。从看似简单的形状,直角三角形,我们获得了工具和见解,帮助我们进行实际和理论上的努力。直角三角形、圆形、正弦波和指数曲线之间的微妙数学关系,只有在建立了坚实的三角学基础之后才能完全理解。
应用

由于许多物理问题可以用三角形来表达,因此三角学在物理科学和工程领域得到了广泛的应用。
三角学是测量和建筑所必需的,因为三角形中的长度和角度之间的关系直接使用。
土木工程师、机械工程师和物理学家使用三角学来理解力如何施加以及不同的物体在互相推或碰撞时将朝哪个方向运动。

由于三角函数映射到圆,而圆映射到波(我们将解释这一切是如何工作的!),电气工程师使用三角学来进行有关他们所处理的波形模式的计算,例如从墙壁上出来的交流电或手机的无线电信号。
电影和电子游戏中出现的计算机图形实际上是在你的屏幕上渲染了数百万个小三角形,尽管之后还有一些小技巧让画面看起来更加流畅和圆滑。







