三角学/勾股定理

在一个直角三角形中
斜边的平方
等于
另外两条边的平方和。

可汗学院

视频链接

可汗学院 有关于这个主题的视频资料，你可能会更容易理解。

• 勾股定理，给出了定理。
• 勾股定理 II，对这个主题进行了练习。

定理

直角三角形

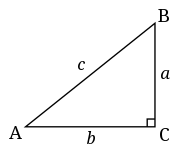
在一个直角三角形（直角三角形）中，最长的边总是离直角最远。它被称为斜边。斜边的长度可以从另外两条边的长度计算出来。在图中，c 是斜边，我们可以用a 和b 来计算它。

这是一个关于勾股定理或毕达哥拉斯定理的陈述 - 作为将边长a、b 和c 联系起来的等式：

$a^{2}+b^{2}=c^{2}$

其中c 代表斜边的长度，a 和b 代表另外两条边的长度。

这仅适用于直角三角形！

对于直角三角形，其角点用 A、B、C 表示，如下所示，以下表示的是同一个意思。

${\overline {BC}}^{2}+{\overline {AC}}^{2}={\overline {AB}}^{2}$

我们只是用不同的符号表示边长a、b 和c。

---

几何解释

勾股定理：两条直角边（a 和b）上正方形的面积之和等于斜边（c）上正方形的面积。

我们也可以用右侧的图来表示这个等式，其中直角三角形的每一侧都有一个正方形连接到它。这是勾股定理的几何解释，将定理视为关于面积的定理。较小的正方形的面积加起来等于较大正方形的面积。

就面积而言，勾股定理指出

在任何直角三角形中，以斜边（与直角相对的边）为边的正方形的面积等于以两条直角边（两条在直角处交汇的边）为边的正方形的面积之和。

关于勾股定理的两种说法完全相同，因为正方形的面积只是其中一边的长度的平方。

定理的历史

毕达哥拉斯， изображенный на монете III века

勾股定理以希腊数学家毕达哥拉斯命名，根据传统，他被认为是该定理的发现者和证明者，尽管人们经常争论说关于该定理的知识早于他。有许多证据表明巴比伦数学家理解了这个公式。

三个实例

在一个直角三角形中
斜边的平方
等于
另外两条边的平方和。

例子 1 勾股定理的一个常用例子是直角三角形，其中 $a=3$ 和 $b=4$，因为数字计算出来非常漂亮 ${\begin{matrix}a^{2}+b^{2}&=&\\3^{2}+4^{2}&=&\\9+16&=&25\end{matrix}}$ 所以 $c^{2}=25$ 和 $c={\sqrt {25}}$ 和 $c=5$

示例 2 另一个常用的例子是一个直角三角形，其中另外两个角分别是 $45^{\circ }$，且$a=1$ 和 $b=1$。这次答案不是一个整数 ${\begin{matrix}a^{2}+b^{2}&=&\\1^{2}+1^{2}&=&\\1+1&=&2\end{matrix}}$ 所以 $c^{2}=2$ 和 $c={\sqrt {2}}$ 我们可以就此止步，或者给出答案的小数形式。 $c\approx 1.414$ 符号 $\approx$ 表示“近似”。

示例 3 另一个例子是一个直角三角形，其中较短的边分别是 $p=11$ 厘米 和 $q=7$ 厘米。 关于 $p$ 和 $q$ 是什么呢？只要我们保持一致，使用什么字母来命名边的长度并不重要。蓝色框中的公式仍然成立。在这种情况下，我们可以将斜边称为 $r$，因此我们有 $p^{2}+q^{2}=r^{2}$。 ${\begin{matrix}p^{2}+q^{2}&=&\\11^{2}+7^{2}&=&\\121+49&=&170\end{matrix}}$ 所以 $r^{2}=170$ 和 $r={\sqrt {170}}$ 厘米 并将答案以小数形式给出。 $r\approx 13.04$ 厘米 答案合理吗？ 值得检查一下答案是否合理。如果短边分别为 11 厘米和 7 厘米，长边约为 13 厘米是否合理？是的，很合理。如果你得到的结果是 20 厘米（或 170 厘米），那就不合理了。另外两条边无法延伸那么远。或者，如果答案是 11 厘米或更小，你就知道你没有得到斜边的长度，即最长边。我们这里得到的结果是 13.04 厘米，这是合理的，我们可能应该将其四舍五入到 13 厘米。

三维

勾股定理在三维空间中将对角线 AD 与三个边联系起来。

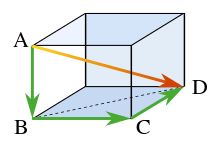
勾股定理可以应用于三维空间，如下所示。

考虑图中所示的矩形体。矩形体底面上的对角线 *BD* 的长度可以通过勾股定理求得，公式如下：

${\overline {BD}}^{2}={\overline {BC}}^{2}+{\overline {CD}}^{2}$

其中这三条边构成直角三角形。使用水平对角线 *BD* 和垂直边 *AB*，对角线 *AD* 的长度可以通过第二次应用勾股定理求得，公式如下：

${\overline {AD}}^{2}={\overline {AB}}^{2}+{\overline {BD}}^{2}$

或者，一步完成：

${\overline {AD}}^{2}={\overline {AB}}^{2}+{\overline {BC}}^{2}+{\overline {CD}}^{2}$

这个结果是对角线 ${\overline {AD}}$ 关于三个互相垂直边的三维表达式。

这个一步完成的公式可以看作是勾股定理对更高维度的推广。然而，这个结果实际上只是对原始勾股定理的重复应用。

卡夫拉金字塔

一个三维的例子 卡夫拉金字塔；高 274 肘；底面 412 x 412 肘 用于计算倾斜边 *AC* 长度的线条和标签 这个例子是三维的，我们再次需要使用勾股定理两次。 卡夫拉大金字塔高 274 肘，底面为正方形，边长为 412 肘。从一个角到顶点的倾斜对角线边的长度是多少？ 要回答这个问题，我们分两个阶段进行。请看图示。 直线 ${\overline {AO}}$ 是垂直的，直线 ${\overline {OB}}$ 是水平的，因此存在一个直角三角形，其边长为 ${\overline {AO}}$ 和 ${\overline {OB}}$。这使我们能够计算长度 ${\overline {AB}}$。 我们需要小心。 ${\overline {AO}}$ 是 274 肘，但 ${\overline {OB}}$ 是正方形边长的一半，所以 ${\overline {OB}}$ 是 ${\tfrac {412}{2}}=206$ 肘。 三角形 $\triangle AOB$ 的斜边 ${\overline {AB}}$ 的长度是多少？那么， ${\begin{matrix}{\overline {AO}}^{2}+{\overline {OB}}^{2}&=&\\274^{2}+206^{2}&=&\\75,076+42,436&=&117,512\end{matrix}}$ 所以 ${\overline {AB}}^{2}=117,512$ 和 ${\overline {AB}}={\sqrt {117,512}}$ 肘 我们已经取得了进展，但我们想要的是长度 ${\overline {AC}}$，而不是长度 ${\overline {AB}}$。 现在我们有另一个直角三角形，$\triangle ABC$，直角在 B 点。我们要求线段 ${\overline {AC}}$ 的长度。我们刚刚计算了 ${\overline {AB}}$ 的长度，并且我们知道，因为金字塔的底面是一个正方形，所以 ${\overline {BC}}$ 再次是 206 肘尺。这次 ${\overline {AC}}$ 是斜边（$\triangle ABC$ 的斜边）。所以 $\displaystyle {\begin{matrix}{\overline {AB}}^{2}+{\overline {BC}}^{2}&=&\\{\sqrt {117,512}}^{2}+206^{2}&=&\\117,512+42,436&=&159,948\end{matrix}}$ 所以 ${\overline {AC}}^{2}=159,948$ 和 ${\overline {AC}}={\sqrt {159,948}}$ 肘尺 ${\overline {AC}}\approx 400$ 肘尺

其他形式

如引言中所述，如果 c 表示斜边的长度，a 和 b 表示另外两边的长度，则勾股定理可以表示为勾股方程

$a^{2}+b^{2}=c^{2}$

或者，解出 c

$c={\sqrt {a^{2}+b^{2}}}$

这就是我们在上面所有例子中所做的。我们利用较短的边来计算斜边的长度。

如果已知斜边 c，并且需要找到其中一条直角边的长度，则可以使用以下公式

$b={\sqrt {c^{2}-a^{2}}}$

或者

$a={\sqrt {c^{2}-b^{2}}}$

勾股方程提供了一个关于直角三角形三条边的简单关系，因此如果已知任意两条边的长度，则可以求出第三条边的长度。

练习

一个立方体盒子用来运输一台打印机。如果一边长 90 厘米，盒子中任意两个顶点之间的最长距离是多少？

一个液晶电视屏幕从角到角测量为 26 英寸。屏幕高度为 13 英寸。屏幕宽度是多少？（精确到十分之一英寸）

该图中，最长线的长度是多少？ 勾股定理的再现 在此问题中，您可以假设所有看起来像直角的角都是直角。

来自四维空间的外星人正在将他们的全息电视装箱，准备前往地球。盒子尺寸为 1.5 埃 by 1.5 埃 by 1.5 埃 by 1.5 埃（它是一个 4 维超立方体）。最长对角线的长度是多少？

如果一个房间长 17 英尺，宽 14 英尺，高 10 英尺，那么(a)地板、(b)一端墙壁和(c)房间侧壁的对角线长度是多少？

找到缺失的边（毕达哥拉斯三元组） 在这些例子中，你都被告知 三角形的三边都是整数。 三角形是一个直角三角形 你被告知了两边。 找到第三边。哪边是斜边？ 你被告知的边是 4、5，第三边是多少？ 你被告知的边是 5、12，第三边是多少？ 你被告知的边是 6、8，第三边是多少？ 你被告知的边是 40、41，第三边是多少？

平方小数 $(-0.5)^{2}$ 是多少？ 在 -2 到 +2 之间的数字中，哪些数字平方后更接近于零？