三角学/证明：勾股定理

在直角三角形中
斜边的平方
等于
另外两边的平方之和。

通常称为：$c^{2}=a^{2}+b^{2}$ （其中 $c$ 是斜边）或 ${\text{hyp}}^{2}={\text{leg}}^{2}+{\text{leg}}^{2}$

这个定理可能比任何其他定理都有更多已知的证明；这本书《勾股定理》包含 370 种证明。^[1]

减法证明

使用四个相同直角三角形面积减法的证明

此证明使用重新排列。该图显示了两个相同的边长为 $a+b$ 的大方形。

• 顶部方形包含斜边上的方形加上四个相同直角三角形，位于它的四个角。
• 在底部，相同的方形包含另外两边上的方形加上相同的四个直角三角形，现在移动到形成两个长方形，边长为 $a,b$ ，位于底部两个角。

从两个相同的方形中，边长为 $a,b,c$ 的相同的四个直角三角形的面积被减去（彩色）。减去三角形会从面积相等的方形中移除相同的（彩色）面积，因此剩余的白色区域，$c^{2}$ 和 $a^{2}+b^{2}$，是相等的。

...就是这样！

欧几里得的证明

欧几里得《几何原本》中的证明

欧几里得的证明要复杂得多，它依赖于将图形细分为各个部分并表明这些部分是全等的。这是一个数学史的片段。你不必记住这个证明。事实上，如果你第一次读这本书，完全可以跳过它，直接进入“练习：拼图三角形”。

为什么这个证明在这里？部分原因是为了表明证明事物的方法不止一种。部分原因是，欧几里得非常谨慎地以小步进行，他之前已经证明了每一步。在“减法证明”中，我们使用了关于面积及其组成部分如何组合的知识，这些知识是真实的，但我们还没有真正证明过。

概括来说，欧几里得《几何原本》中的证明是这样的。方形被分成左右两个长方形。构建一个三角形，它的面积是左长方形的一半。然后构建另一个三角形，它的面积是左边的方形的一半。表明这两个三角形是全等的，证明了这个方形与左长方形面积相同。这个论点之后是关于右边长方形和剩余方形的类似版本。将两个长方形组合在一起以重新形成斜边上的方形，它的面积等于另外两个方形面积之和。细节如下。

设 $A,B,C$ 是直角三角形的三个顶点，直角位于 $A$。从 $A$ 向斜边上的方形的相对边画垂线。这条线将斜边上的方形分成两个长方形，每个长方形的面积都与一条腿上的方形面积相同。

对于形式证明，我们需要四个基本的引理（证明完整证明的一步）

1. 如果两个三角形有两条边分别相等，并且包含这两条边的角相等，那么这两个三角形是全等的（边角边）。
2. 三角形的面积等于以相同底边且具有相同高的任何平行四边形的面积的一半。
3. 长方形的面积等于两条相邻边的乘积。
4. 方形的面积等于其两条边的乘积（来自 3）。

接下来，每个顶部的正方形都与一个三角形相等，该三角形又与构成底部正方形的两个矩形之一相等。

包括新线条的插图

证明如下：

1. 令$\triangle ACB$ 为一个直角三角形，直角为 $\angle CAB$ 。
2. 在每条边 $BC,AB,CA$ 上绘制正方形，依次为 $CBDE,BAGF,ACIH$ 。绘制正方形需要欧几里得的先前定理，并且依赖于平行公设。
3. 从 $A$ 作一条平行于 $BD$ 和 $CE$ 的直线。该直线将垂直地与 $BC$ 和 $DE$ 相交于 $K$ 和 $L$ ，分别。
4. 连接 $CF$ 和 $AD$ ，形成三角形 $\triangle BCF,\triangle BDA$ 。
5. $\angle CAB,\angle BAG$ 都是直角；因此 $C,A,G$ 共线。类似地，$B,A,H$ 共线。

证明矩形 $BDLK$ 和正方形 $BAGF$ 面积的一半的两个全等三角形

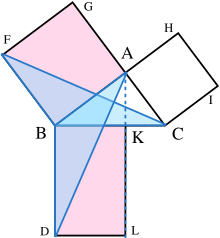
1. 角 CBD 和 FBA 都是直角；因此角 ABD 等于角 FBC，因为两者都是直角和角 ABC 的和。
2. 由于 AB 和 BD 分别等于 FB 和 BC，因此三角形 ABD 必须与三角形 FBC 全等。
3. 由于 A 与 K 和 L 共线，因此矩形 BDLK 的面积必须是三角形 ABD 的两倍，因为它与 BK 共高，与 BD 共底，而三角形的面积是其底和高的积的一半。
4. 由于 C 与 A 和 G 共线，因此正方形 BAGF 的面积必须是三角形 FBC 的两倍。
5. 因此，矩形 BDLK 的面积必须等于正方形 BAGF 的面积 = AB²。
6. 类似地，可以证明矩形 CKLE 的面积必须等于正方形 ACIH 的面积 = AC²。
7. 将这两个结果相加，得 AB² + AC² = BD × BK + KL × KC。
8. 由于 BD = KL，因此 BD* BK + KL × KC = BD(BK + KC) = BD × BC。
9. 因此 AB² + AC² = BC²，因为 CBDE 是一个正方形。

…我们完成了。

这个证明出现在欧几里得的《几何原本》中，作为第 1 卷第 47 题的证明，它证明了斜边上的正方形的面积等于另外两个正方形的面积之和。

鸣谢

• 感谢维基百科页面 勾股定理 提供了本页面的初始版本。更多注释和参考资料请参见该页面。