三角学/勾股定理

在一个直角三角形中
斜边的平方
等于
另外两边的平方和。

可汗学院

视频链接

可汗学院提供了与本主题相关的视频资料，您可能会发现这些资料更容易理解

• 勾股定理，介绍了定理本身。
• 勾股定理 II，提供了有关本主题的练习解题过程。

定理

直角三角形

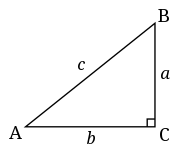
在一个直角三角形中（直角三角形），最长的边总是距离直角最远的边。它被称为斜边。斜边的长度可以通过另外两边的长度计算得出。在图中，c 是斜边，我们可以通过a 和b 计算得出。

这是一个勾股定理或毕达哥拉斯定理的陈述 - 作为连接边长a、b 和c 的方程式：

$a^{2}+b^{2}=c^{2}$

其中c 表示斜边的长度，a 和b 表示另外两边的长度。

这仅适用于直角三角形！

对于直角三角形，其角点分别标记为 A、B、C，如下所示，以下表达意味着相同的内容

${\overline {BC}}^{2}+{\overline {AC}}^{2}={\overline {AB}}^{2}$

我们只是对边a、b 和c 使用了不同的符号。

---

几何解释

勾股定理：两条直角边（a 和b）上正方形的面积之和等于斜边（c）上正方形的面积。

我们也可以用图示来展示这个方程式，如图所示，直角三角形的每条边都连接着一个正方形。这是勾股定理的几何解释，从面积的角度来看这个定理。较小的正方形的面积加起来等于较大正方形的面积。

从面积的角度来看，勾股定理说明

在任何直角三角形中，以斜边为边的正方形的面积（与直角相对的边）等于以两条直角边为边的正方形的面积之和。

关于勾股定理的两种说法完全相同，因为正方形的面积就是边长的平方。

定理的历史

毕达哥拉斯，描绘在一枚公元 3 世纪的硬币上

勾股定理以希腊数学家毕达哥拉斯的名字命名，传统上他被认为发现了并证明了这个定理， 尽管人们经常争论说对这个定理的认识早于他。有许多证据表明巴比伦数学家了解这个公式。

三个解题示例

在一个直角三角形中
斜边的平方
等于
另外两边的平方和。

示例 1 勾股定理的常用示例是直角三角形，其中 $a=3$ 和 $b=4$，因为数字计算结果非常简洁 ${\begin{matrix}a^{2}+b^{2}&=&\\3^{2}+4^{2}&=&\\9+16&=&25\end{matrix}}$ 所以 $c^{2}=25$ 和 $c={\sqrt {25}}$ 和 $c=5$

示例 2 另一个常用的例子是直角三角形，其中另外两个角是 $45^{\circ }$，并且 $a=1$ 和 $b=1$。这次答案不是整数。 ${\begin{matrix}a^{2}+b^{2}&=&\\1^{2}+1^{2}&=&\\1+1&=&2\end{matrix}}$ 所以 $c^{2}=2$ 和 $c={\sqrt {2}}$ 我们可以停在这里，也可以给出答案的小数形式。 $c\approx 1.414$ $\approx$ 符号表示“大约”。

示例 3 另一个例子是直角三角形，其中较短的边是 $p=11$ 厘米和 $q=7$ 厘米。 关于 $p$ 和 $q$ 呢？我们用什么字母来表示边的长度并不重要，只要我们保持一致就行。蓝色方框中的公式仍然适用。在这种情况下，我们可以将斜边称为 $r$，因此我们有 $p^{2}+q^{2}=r^{2}$。 ${\begin{matrix}p^{2}+q^{2}&=&\\11^{2}+7^{2}&=&\\121+49&=&170\end{matrix}}$ 所以 $r^{2}=170$ 和 $r={\sqrt {170}}$ 厘米 并给出答案的小数形式。 $r\approx 13.04$ 厘米 这个答案合理吗？ 值得检查一下答案是否合理。如果短边是 11 厘米和 7 厘米，长边大约是 13 厘米是否合理？是的，很合理。如果你得到 20 厘米（或 170 厘米）的答案，它将是不合理的。另外两条边不会延伸那么远。或者如果答案是 11 厘米或更小，你就会知道你没有得到斜边的长度，即最长的边。这里 13.04 厘米的答案是可以接受的，我们可能应该四舍五入到 13 厘米。

三维空间中

勾股定理在三维空间中将对角线 AD 与三条边联系起来。

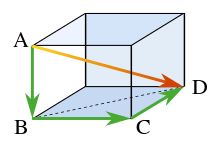
勾股定理可以应用于三维空间，方法如下。

考虑图中所示的矩形体。矩形体底面上的对角线 BD 的长度可以用勾股定理求得，如下所示：

${\overline {BD}}^{2}={\overline {BC}}^{2}+{\overline {CD}}^{2}$

其中这三条边构成一个直角三角形。使用水平对角线 BD 和垂直边 AB，对角线 AD 的长度可以通过第二次应用勾股定理求得，如下所示：

${\overline {AD}}^{2}={\overline {AB}}^{2}+{\overline {BD}}^{2}$

或者，一步到位：

${\overline {AD}}^{2}={\overline {AB}}^{2}+{\overline {BC}}^{2}+{\overline {CD}}^{2}$

此结果是对角线 ${\overline {AD}}$ 关于三个相互垂直边的三维表达式。

这个一步公式可以看作是勾股定理在更高维度的推广。然而，这个结果实际上只是对原始勾股定理的重复应用。

卡夫拉金字塔

一个三维空间中的例子 卡夫拉金字塔；高 274 肘；底面为 412 x 412 肘 用于计算斜边 AC 长度的线条和标签 这个例子是在三维空间中的，我们又必须两次使用勾股定理。 卡夫拉大金字塔高 274 肘。它有一个正方形底座，正方形边长为 412 肘。从一个角到顶点的斜对角边的长度是多少？ 要回答这个问题，我们分两个阶段进行。请看图。 线 ${\overline {AO}}$ 是垂直的，线 ${\overline {OB}}$ 是水平的，因此存在一个直角三角形，其边为 ${\overline {AO}}$ 和 ${\overline {OB}}$。这使我们能够计算长度 ${\overline {AB}}$。 我们需要小心。 ${\overline {AO}}$ 是 274 肘，但 ${\overline {OB}}$ 是正方形边长的一半，所以 ${\overline {OB}}$ 是 ${\tfrac {412}{2}}=206$ 肘。 三角形 $\triangle AOB$ 的斜边 ${\overline {AB}}$ 的长度是多少？嗯， ${\begin{matrix}{\overline {AO}}^{2}+{\overline {OB}}^{2}&=&\\274^{2}+206^{2}&=&\\75,076+42,436&=&117,512\end{matrix}}$ 所以 ${\overline {AB}}^{2}=117,512$ 和 ${\overline {AB}}={\sqrt {117,512}}$ 肘 我们取得了进展，但我们需要 ${\overline {AC}}$ 的长度，而不是 ${\overline {AB}}$ 。 现在我们又有一个直角三角形，$\triangle ABC$ ，在 B 点有一个直角。我们需要 ${\overline {AC}}$ 的长度。我们刚刚计算了 ${\overline {AB}}$ ，我们知道，因为金字塔的底座是正方形，所以 ${\overline {BC}}$ 再次是 206 肘。这次 ${\overline {AC}}$ 是斜边（$\triangle ABC$）。所以 $\displaystyle {\begin{matrix}{\overline {AB}}^{2}+{\overline {BC}}^{2}&=&\\{\sqrt {117,512}}^{2}+206^{2}&=&\\117,512+42,436&=&159,948\end{matrix}}$ 所以 ${\overline {AC}}^{2}=159,948$ 和 ${\overline {AC}}={\sqrt {159,948}}$ 肘 ${\overline {AC}}\approx 400$ 肘

其他形式

如引言中所述，如果 *c* 表示斜边的长度，*a* 和 *b* 表示其他两边的长度，则勾股定理可以表示为勾股方程

$a^{2}+b^{2}=c^{2}$

或者，解出 *c*

$c={\sqrt {a^{2}+b^{2}}}$

这就是我们在上面所有示例中所做的。我们正在使用较短的边来计算斜边的长度。

如果已知斜边 *c*，并且必须找到其中一条边的长度，则可以使用以下等式

$b={\sqrt {c^{2}-a^{2}}}$

或者

$a={\sqrt {c^{2}-b^{2}}}$

勾股方程提供了直角三角形三边之间的简单关系，因此，如果已知任意两边的长度，就可以找到第三边的长度。

练习

一个立方体盒子用来运送打印机。如果一边是 90 厘米，那么盒子的两个角之间的最长距离是多少？

一台 LCD 电视屏幕从角到角测量为 26 英寸。屏幕高度为 13 英寸。屏幕有多宽？（精确到十分之一英寸）

此图中，最长线的长度是多少？ 勾股定理再次出现 在此问题中，您可以假设所有看起来像直角的角都是直角。

来自四维空间的外星人正在将他们的全息电视包装到一个盒子里，准备前往地球。该盒子测量为 1.5 埃 by 1.5 埃 by 1.5 埃 by 1.5 埃（这是一个四维超立方体）。最长对角线的长度是多少？

如果一个房间长 17 英尺，宽 14 英尺，高 10 英尺，那么（a）地板，（b）一端墙壁，以及（c）房间侧墙的对角线的长度是多少？

找到缺失的边（勾股数） 在这些示例中，您都被告知 三角形的三条边都是整数。 三角形是直角三角形 您得到了两条边。 找到第三条边。哪条边是斜边？ 您被告知的边是 4,5，第三条边是多少？ 您被告知的边是 5,12，第三条边是多少？ 您被告知的边是 6,8，第三条边是多少？ 您被告知的边是 40,41，第三条边是多少？

平方小数 $(-0.5)^{2}$ ? 在 -2 和 +2 之间的数字中，哪些数字平方后更靠近零？