- 另见: 微积分/函数, 离散数学/函数和关系
函数是另一种用数学方法描述某些事物的途径。它们通常被描述为一个两端开口的盒子中的机器;你从一端放入一些东西,在中间发生一些事情,然后从另一端出来一些东西。函数是盒子内部的机器,它由它对任何输入执行的操作定义。
假设机器有一个刀片,它会将你放入的任何东西切成两半,并将其中一半从另一端送出。如果你放进去一根香蕉,你就会得到半根香蕉。如果你放进去一个苹果,你就会得到半个苹果。
关于这台机器的一个好问题可能是,另一半水果发生了什么?但是,由于这是代数,进入和走出函数的东西将是数字,因此我们很确定盒子不会被数字填满并破裂。让我们将该函数定义为接受你的输入并将其切成两半,即除以二。如果你放入 2,你将得到 1。如果你放入 57,你将得到 28.5。函数机器允许我们改变表达式。函数通常用单个字母命名。我们将这个叫做 h,代表 half(一半)。(我们选择的字母没有什么特别之处——我们也可以称这个函数为 f。这个字母不必代表任何东西。)
现在我们需要符号。要将 2 放入函数中,我们写  (读作 h of 2)。我们知道
(读作 h of 2)。我们知道

我们还可以计算

使用代数符号,我们可以描述这台机器的功能为

与其列出我们可以放入机器的所有东西,我们用变量  来表示它们。当我们写
来表示它们。当我们写  时,我们的意思是我们将
时,我们的意思是我们将  送入机器,它被切成两半。使用这种形式,我们不必计算当我们放入 57 个苹果或橘子时从机器出来的半数。我们知道,当我们将 57 或任何东西放入我们的机器时,只有 28.5 这些东西会从另一端出来。当使用代数符号来指定关系时;我们创建了一些称为代数函数定义的东西。(这个例子说明了数学与科学和工程之间的区别。由于这是一个假想的机器,我们只需要指定从盒子另一端出来的是什么。在真实的机器中,我们还需要考虑如何处理没有从另一端出来的部分)。
送入机器,它被切成两半。使用这种形式,我们不必计算当我们放入 57 个苹果或橘子时从机器出来的半数。我们知道,当我们将 57 或任何东西放入我们的机器时,只有 28.5 这些东西会从另一端出来。当使用代数符号来指定关系时;我们创建了一些称为代数函数定义的东西。(这个例子说明了数学与科学和工程之间的区别。由于这是一个假想的机器,我们只需要指定从盒子另一端出来的是什么。在真实的机器中,我们还需要考虑如何处理没有从另一端出来的部分)。
在指数中使用 ^
函数也可以被认为是关系的子集。关系是集合中数字之间的联系。

换句话说,你输入的每个数字都与你输出的每个数字相关联。区别在于在函数中,每个“输入”数字都与一个“输出”数字相关联,而在关系中,“输入”数字可能与多个或零个“输出”数字相关联。这是关于函数的一个重要事实。请注意,上面图表中所示的关系不是函数,因为它不满足此要求,不像下面第二个图表中所示的关系,它是一个函数。
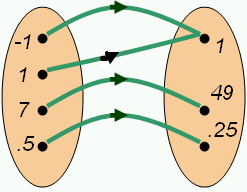
所有函数都是关系。并非所有关系都是函数。
函数的定义域是指该函数定义的“输入”数字的集合。定义域是函数定义的一部分。在上图中的函数中,定义域是{-1,1,7,1/2}。
自然定义域是指代数定义的函数中,函数定义的数字的集合。
在大多数代数公式中,x 通常是与定义域相关的变量。
例子
函数  的定义域是
的定义域是  ,因为平方根函数仅在正数时有定义(假设我们只处理实数)。
,因为平方根函数仅在正数时有定义(假设我们只处理实数)。
函数的值域是指对于给定输入,方程的结果或解的集合。一个真正的函数对于每个定义域值只有一个结果。
在大多数代数公式中,y 通常是与值域相关的变量。因此,它也可以表示为f(x),表示它的值是x 的函数。
例子
函数  的值域是
的值域是  ,因为数字的平方总是正数。
,因为数字的平方总是正数。
同时考虑定义域和值域,函数是指任何数学公式,对于每个输入值都产生一个且仅一个结果。因此,可以说在一个有效的函数中,定义域 (x) 和值域 (y) 具有多对一的关系,因此对于每个给定的定义域值,只有一个值域值作为结果,但反过来不一定如此。这是有道理的,因为结果可以重复,但输入不能重复。
因此,如果 x 是水平方向,y 是垂直方向,那么以 y 为自变量的函数(例如 y = mx + b)将产生一组结果,使得如果在 图 上的任何点处用垂直线与之相交,它将只穿过图形一次。渐近函数(至少有一个未定义结果)也被认为是有效的,因为它没有穿过图形的多个点。这被称为“垂直线”测试。
定义域和值域这两个术语可以应用于所有关系,而不仅仅是函数。关系是指在一个定义中,定义域中的一个元素映射到值域中的多个元素。我们使用定义域和值域这两个术语来定义函数和关系之间的区别。
在谈论或书写函数时,不同的术语被用来描述函数如何工作或它们的功能。
当我们写  时,我们说 f of x。因此,如果我们有一个用方程
时,我们说 f of x。因此,如果我们有一个用方程  定义的函数,那么我们说
定义的函数,那么我们说
g of x 等于 x 和 2 的和除以 7。
或者
g of x 是 x 加 2 全部除以 7。
当我们将一个值(比如 5)代入函数中的 x 时,我们写  ,但我们说
,但我们说
g of 5 等于 1.
代数符号是数学家表达由算术运算符定义的关系的最简单方法,如  指数和根式。一旦定义了其中一些函数,用函数名和上述函数值进行引用就更容易了。
指数和根式。一旦定义了其中一些函数,用函数名和上述函数值进行引用就更容易了。
如果我们有一个用方程  定义的函数,那么我们说 g 在 x 处的函数值是 x 和 2 的和除以 7。 这样,
定义的函数,那么我们说 g 在 x 处的函数值是 x 和 2 的和除以 7。 这样,
一个函数,其定义取决于输入。
f(x)=|x|
或者

可以将  解释为 x 和 0 之间的无向距离(始终是非负的)。继续,
解释为 x 和 0 之间的无向距离(始终是非负的)。继续, 可以解释为数轴上数字 x 和 y 之间的距离。
可以解释为数轴上数字 x 和 y 之间的距离。
偶函数定义为一个函数  ,满足
,满足  。
。
从几何意义上讲,偶函数可以定义为关于 y 轴(穿过原点的垂直线)具有镜像对称性的函数。
偶函数的一个例子是  ,因为
,因为  ,并且因为对于所有实数 x,都有
,并且因为对于所有实数 x,都有  。
。
奇函数定义为一个函数  ,满足
,满足  。
。
从几何意义上讲,奇函数可以定义为关于原点具有 180 度旋转对称性的函数。
一个 奇 函数的例子是  ,因为对于所有实数 x,都有
,因为对于所有实数 x,都有  ,例如
,例如 
复合函数  可以定义为两个函数
可以定义为两个函数  和
和  的复合,记为
的复合,记为  (读作 h of x 等于 f of g of x)或
(读作 h of x 等于 f of g of x)或  。
。

例子
Let 




 ∴
∴
例子
Let 





 Domain:
Domain:  Range:
Range: 
函数  是一个一对一函数
是一个一对一函数  的反函数,当且仅当以下条件成立
的反函数,当且仅当以下条件成立


函数  的逆函数用
的逆函数用  表示。
表示。
从几何角度来看, 是
是  关于直线
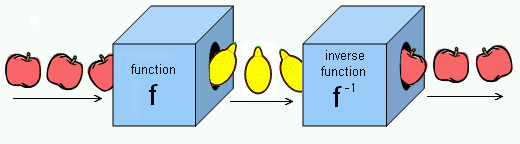
关于直线  的镜像。从概念上讲,使用 *盒子* 类比,函数的逆函数盒子 *撤销* 函数常规盒子的操作。
的镜像。从概念上讲,使用 *盒子* 类比,函数的逆函数盒子 *撤销* 函数常规盒子的操作。
 例子
例子








要找到函数的逆函数,请记住,当我们使用  作为
作为  的输入时,结果是
的输入时,结果是  。因此,首先写下
。因此,首先写下  并求解
并求解  。
。
例子
Suppose: Then
Then 



逆函数的定义域与原函数的值域完全相同。如果原函数的值域受到某种限制,则逆函数需要一个受限的定义域。
例子





 The Range of
The Range of  is
is  . So the Domain of
. So the Domain of  is
is  .
.
对于每个输入都存在一个唯一输出的函数。
等价地,我们可以说函数  被称为 *一一函数*,如果对于所有
被称为 *一一函数*,如果对于所有  意味着
意味着  ,其中 *A* 是 *f* 的定义域集合,*x* 和 *x'* 都是该集合的成员。
,其中 *A* 是 *f* 的定义域集合,*x* 和 *x'* 都是该集合的成员。
水平线测试
如果没有任何水平线与函数图交于一个以上的位置,则该函数为一一函数。
在上一章中,我们回顾了你已经了解的数学知识:数字、变量和关系。我们回顾了数字的类型、对数字可以执行的操作、这些操作的性质以及这些性质如何让你写出表达式,或者如果我们对表达式足够了解,你可以写出定义真实事物的方程和不等式。
在上面的部分中,我们已经了解了函数的概念。首先,我们展示了如何在等号运算符的一侧创建函数,而在另一侧创建表达式。然后,我们查看了使用函数符号的更复杂方法。
一旦你习惯了它们,函数就会让你以不同的方式看待数学。当你用数字思考数学时,你只是在思考一个答案。当你用函数思考数学时,你是在寻找关系,并且你在建立数学模型。
举一个 3x3 平方格和对角线的例子。对角线上的三角形面积是多少?应用面积函数:l x w,然后应用一半函数。










































































