当我们看到一个像  这样的函数时,我们称我们正在改变的变量——在本例中是
这样的函数时,我们称我们正在改变的变量——在本例中是  --为自变量。我们将函数的值赋给一个我们称为因变量的变量。我们说
--为自变量。我们将函数的值赋给一个我们称为因变量的变量。我们说  是自变量的原因是,我们可以为函数定义的任何值选择——在本例中是实数
是自变量的原因是,我们可以为函数定义的任何值选择——在本例中是实数  是隐含的——作为函数的输入。一旦我们选择自变量的值,函数就会始终输出相同的结果。我们说结果被赋予因变量,因为它取决于我们放入函数中的值。
是隐含的——作为函数的输入。一旦我们选择自变量的值,函数就会始终输出相同的结果。我们说结果被赋予因变量,因为它取决于我们放入函数中的值。
将  与我们的函数
与我们的函数  等同,则
等同,则  则
则  则
则 
自变量现在是  而因变量是
而因变量是 
- 注意:这是一个非常不常见的情况,其中有序对
 被反向映射
被反向映射  以及相应的反转(因变量,自变量),(值域,定义域),现在
以及相应的反转(因变量,自变量),(值域,定义域),现在  必须对于每个
必须对于每个  都是唯一的,对应于函数的水平线检验!旋转或交换轴的位置、坐标对
都是唯一的,对应于函数的水平线检验!旋转或交换轴的位置、坐标对  和(横坐标,纵坐标)的顺序将是不好的。
和(横坐标,纵坐标)的顺序将是不好的。
我们是否使用了代数来改变函数的性质?让我们看看三个函数的结果
 |
 |
 |
 |
 |
 |

|
 |

|
 |

|
|
 |
 |
 |

|
 |

|
 |

|
|
 |

|
 |

|
 |

|
 |

|
|
如果我们观察上面的表格,我们可以看到  的自变量给出的结果与
的自变量给出的结果与  的因变量相同。当我们查看
的因变量相同。当我们查看  的值时,我们可以看到这意味着什么。函数
的值时,我们可以看到这意味着什么。函数  与函数
与函数  相同,但是当我们在
相同,但是当我们在  和
和  之间切换我们使用的自变量时,我们发现
之间切换我们使用的自变量时,我们发现  和
和  是互逆函数。
是互逆函数。
让我们看看如何在  和
和  中绘制函数,然后回过头来再次看看自变量和因变量的概念。
中绘制函数,然后回过头来再次看看自变量和因变量的概念。
诸如  和
和  这样的变量,可以使用简单的代数来构成一个“关系”。
这样的变量,可以使用简单的代数来构成一个“关系”。 
 和
和  通常用来表示函数。函数记号
通常用来表示函数。函数记号  读作“f of x”,表示一个对自变量
读作“f of x”,表示一个对自变量  具有“显式”依赖关系的函数。通过将变量
具有“显式”依赖关系的函数。通过将变量  赋值为
赋值为 

 现在就成为使用方程记号表示的
现在就成为使用方程记号表示的  的“隐式”函数。如果
的“隐式”函数。如果  是
是  那么
那么  [
[  将表示
将表示  的“显式”函数]。当因变量对于每个自变量值都只有一个值时,关系也是一个函数。
的“显式”函数]。当因变量对于每个自变量值都只有一个值时,关系也是一个函数。
The Cartesian Coordinate System is a uniform rectangular grid used for plane graph plots. It's named after pioneer of analytic geometry, 17th century French mathematician René Descartes, whose Latinized name was Renatus Cartesius. Recall that each point has a unique location, different from every other point. We know that a line is a collection of points. If we pick a direction of travel for the line that starts at a point then all of the other points can be thought of as either behind our starting point or ahead of it. Finally, a plane can be thought of as a collection of lines that are parallel to each other. We can draw another line that is composed of one point from each of the lines that we chose to fill our plane. If we do this then we can locate the other lines as behind or ahead of the line with the point we chose to start on. Descartes decided to pick a line and call it the  -axis, and to then pick a line perpendicular to this line and call it the
-axis, and to then pick a line perpendicular to this line and call it the  -axis. He then labeled this intersection point
-axis. He then labeled this intersection point  and origin O. The points to the left (or behind) of this point each represent a negative number that we label as
and origin O. The points to the left (or behind) of this point each represent a negative number that we label as  The points to the right (or ahead) of this point each represent a positive number that we label as
The points to the right (or ahead) of this point each represent a positive number that we label as  The points on the
The points on the  -axis that are above
-axis that are above  are labeled as positive
are labeled as positive  and the points on the
and the points on the  -axis below
-axis below  are labeled as negative
are labeled as negative  A point is plotted as a location on the plane using its coordinates from the grid formed by the
A point is plotted as a location on the plane using its coordinates from the grid formed by the  and
and  -axes. If you draw a line perpendicular to the
-axes. If you draw a line perpendicular to the  -axis from a point you pick then that point has the same
-axis from a point you pick then that point has the same  -coordinate as the point where that line crosses the
-coordinate as the point where that line crosses the  -axis. If you draw a line perpendicular to the
-axis. If you draw a line perpendicular to the  -axis from your point then it has the same
-axis from your point then it has the same  -coordinate as the point where that line crosses the
-coordinate as the point where that line crosses the  -axis. If you need to sharpen your knowledge in this area, this link/section should help: The Coordinate (Cartesian) Plane
-axis. If you need to sharpen your knowledge in this area, this link/section should help: The Coordinate (Cartesian) Plane
方程及其图形可以被认为是相等的。这是正确的,因为图形是特定方程的表示。这是因为方程是由一个或多个变量以及一个或多个数字和一个等号组成( 
 以及
以及  都是方程的例子)。由于变量被引入作为表示可以代入方程的许多可能数字的一种方式。方程的图形是绘制可以输入的数字(自变量)和可能产生的输出之间关系的一种方式。例如,在方程中:
都是方程的例子)。由于变量被引入作为表示可以代入方程的许多可能数字的一种方式。方程的图形是绘制可以输入的数字(自变量)和可能产生的输出之间关系的一种方式。例如,在方程中:  我们可以选择使
我们可以选择使  成为自变量,并且输出数字每次都将比输入数字大二。该方程的图形将是显示此关系的图片。在图形上,每个
成为自变量,并且输出数字每次都将比输入数字大二。该方程的图形将是显示此关系的图片。在图形上,每个  -值(纵轴)将比代入的(横向)
-值(纵轴)将比代入的(横向)  -值高二,因为方程中的
-值高二,因为方程中的  。
。
本节展示了我们可以用代数方法写出线性函数的不同方法。我们将花一些时间来研究一种称为“斜率截距式”的方法,其方程为 
除非另有说明  的定义域,否则将假定线性函数的定义域为所有实数
的定义域,否则将假定线性函数的定义域为所有实数  ,因此所有线性函数的图形中的直线都无限地向两个方向延伸。此外,在所有实数定义域的线性函数中,线性函数的值域可以覆盖
,因此所有线性函数的图形中的直线都无限地向两个方向延伸。此外,在所有实数定义域的线性函数中,线性函数的值域可以覆盖  的整个实数集,一个例外是当斜率
的整个实数集,一个例外是当斜率  并且函数等于一个常数时。在这种情况下,值域只是该常数。另一种情况是平方函数,当
并且函数等于一个常数时。在这种情况下,值域只是该常数。另一种情况是平方函数,当  时,值域是非负的。
时,值域是非负的。
结果表明,  有无限个解(在英国,
有无限个解(在英国,  也很常见
也很常见 
 以及
以及  )。点
)。点  将被映射到自变量
将被映射到自变量  (假设为横轴)和
(假设为横轴)和  (假设为纵轴)在笛卡尔坐标系上。通过给
(假设为纵轴)在笛卡尔坐标系上。通过给  赋值并计算
赋值并计算  即可找到一个(单个)点坐标解。当
即可找到一个(单个)点坐标解。当  时,根据零积性质,项
时,根据零积性质,项  ,根据加法单位元,项
,根据加法单位元,项  。点
。点  是直线(线性方程的解)中唯一与y轴相交的点。更多关于截距的链接: The
是直线(线性方程的解)中唯一与y轴相交的点。更多关于截距的链接: The  和
和  截距
截距
当我们有方程 时,m告诉我们什么?
时,m告诉我们什么?
[编辑 | 编辑源代码] 是一个常数,称为直线的斜率。斜率表示直线的倾斜程度。
是一个常数,称为直线的斜率。斜率表示直线的倾斜程度。
任意两个不同的点都可以确定一条唯一的直线,并且这条直线包含这两个点。将本研究限制在平面几何( )内,并为唯一点固定坐标,例如
)内,并为唯一点固定坐标,例如  和
和  ,则一条直线就被定义为两个变量之间的关系,它可以用线性方程表示,并可以在图上绘制。当这两个点重合时,即使在同一个平面上,也会产生无限条直线。当
,则一条直线就被定义为两个变量之间的关系,它可以用线性方程表示,并可以在图上绘制。当这两个点重合时,即使在同一个平面上,也会产生无限条直线。当  时,定义的是一条垂直线的关系,而不是一个函数。函数是计算结果为唯一因变量的方程关系。只有当(当且仅当)
时,定义的是一条垂直线的关系,而不是一个函数。函数是计算结果为唯一因变量的方程关系。只有当(当且仅当)  时,包含这两个点的直线才是
时,包含这两个点的直线才是  的线性“函数”。
的线性“函数”。
对于线性函数,可以通过直线上任意两个已知点确定其斜率。斜率对应于直线上任意两个不同点之间垂直方向的增量或变化量除以水平方向的相应增量或变化量。
设  为
为  方向(垂直方向)上的增量或变化量,以及
方向(垂直方向)上的增量或变化量,以及
设  为
为  方向(水平方向)上的增量或变化量。
方向(水平方向)上的增量或变化量。
对于两个点  和
和  ,函数直线的斜率 m 由下式给出:
,函数直线的斜率 m 由下式给出: 
对于线性函数,固定直线上两个唯一的点或固定斜率和直线上任意一点就足以确定这条直线,并用方程表示它。线性函数有一种方程形式,称为直线的点斜式2,它使用斜率  和任意一点
和任意一点  来确定函数直线的有效方程:
来确定函数直线的有效方程: 
代数/斜率
勾股定理和距离公式
代数/标准式和求解斜率
我们将介绍另一种线性函数的一般形式。这就是直线的**截距式**,其中常数a和b使得(a,0)是x截距点,(0,b)是
y截距点。

其中a ≠ 0且b ≠ 0
常数a和b都不能等于0,因为不允许除以0。当线性函数具有简化形式y = m x时,不能应用直线的截距式,因为
y截距纵坐标不能等于0。
用常数a和b乘以直线的截距式将得到

然后它等价于一般线性方程形式A x + B y + C,其中A = b,B = a,C = ab。现在我们看到A和B都不能为0,因此截距式不能表示水平线或垂直线。仅用b乘以直线的截距式得到

如果我们减去

我们得到

这反过来可以重新排列为

这等价于斜截式,其中斜率m = -b/a。
示例:一条绘制的直线在x轴上与-3相交,在y轴上与-6相交。什么方程可以表示这条直线?斜率是多少?
解答:截距式:
乘以-6得到

所以我们看到斜率m = -2。
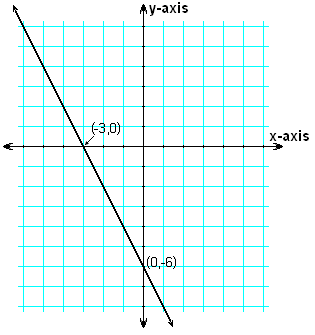 y = - 2x – 6的图形,显示截距。
y = - 2x – 6的图形,显示截距。
该直线也可以写成

示例:方程

能否转换为直线的截距式(x/a) + (y/b) =1来求截距?
解答:不能,任何有效的数学运算都不能将其转换为截距式。而是乘以4,然后减去2x得到

它具有y = m x的形式,其中m = -2。该直线与轴在(0,0)处相交。由于截距均为0,因此不能使用直线的一般截距式。

示例:求连接点(2,1)和(4,4)的直线的斜率和函数。
解答:当根据上述公式从两点计算直线的斜率时,哪一个是点1,哪一个是点2并不重要。让我们将(x1,y1)设为(2,1),将(x2,y2)设为(4,4)。然后使用两点斜率公式m

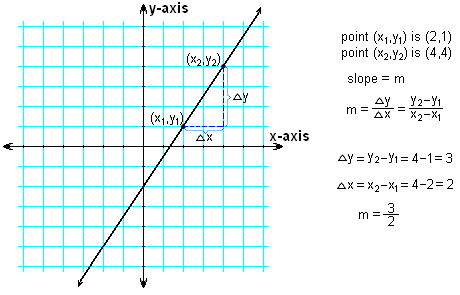
使用点斜式
将任一点的坐标代入点斜式作为x1和y1。为简单起见,我们使用x1=2和y1=1。



使用斜截式
或者,可以在一个变量的线性函数的一般形式y = m x + b中求解y截距纵坐标b。

已知斜率m,取直线上任意一点,并将该点的坐标和m代入线性函数的这种形式,计算b。在本例中,使用(x1,y1)。


现在常数m和b都已知,函数写成

或写成

__________例题结束__________
有关斜率的另一种解释,请参见此处
斜率
例题:画出方程5x + 2y = 10的图像并计算斜率。
解答:这符合线性方程的一般形式,因此找到两个不同的点足以确定直线。要找到x截距,令y = 0并解出x。


所以x截距点为(2,0)。要找到y截距,令x = 0并解出y。


所以y截距点为(0,5)。过(2,0)和(0,5)画一条直线,就会得到以下图形。
 5x + 2y = 10的图像,显示了截距
5x + 2y = 10的图像,显示了截距
要从这两点确定斜率m,可以将(x1,y1)设为(2,0),(x2,y2)设为(0,5),反之亦然,并按如下方式计算

__________例题结束__________
适用于二维笛卡尔坐标系上所有直线的最一般形式是

其中包含三个常数 A、B 和 C。这些常数对于直线来说不是唯一的,因为将整个方程乘以一个常数因子会得到一组新的有效常数,它们对应于同一条直线。当 B = 0 时,方程的其余部分表示一条垂直线,它不是函数。如果 B ≠ 0,则该直线为函数。这种线性函数可以用**斜截式**表示,斜截式包含两个常数。
斜截式

这两个常数 m 和 b 共同唯一地确定一条直线。换句话说,一条特定的直线在这种形式下只能有一对 m 和 b 的值。
这里给出的**点斜式**

使用了三个常数;m 对于给定直线是唯一的;x1 和 y1 不是唯一的,可以是直线上任意一点的坐标。点斜式不能表示垂直线。
这里给出的直线的**截距式**

a ≠ 0 且 b ≠ 0
使用了两个唯一的常数,它们是 x 和 y 截距,但不能用来表示水平线或垂直线,也不能表示穿过 (0,0) 的直线。在本文总结的几种一般形式中,它的适用性最低。
在最后三种线性函数的一般形式中,斜截式是最有用的,因为它只使用给定直线唯一的常数,并且可以表示任何线性函数。本书以及数学中所有问题都可以不使用点斜式或截距式来解决,除非问题中明确要求使用它们。通常,涉及线性函数的问题可以使用斜截式
(y = m x + b) 和斜率公式来解决。
设变量 y 依赖于自变量 x 的函数
 也即
也即 
y 也是函数 f,而 x 也是自变量 ( )。设 y 为表示的商函数

y 的解的图形绘制出一组连续的直线点,**除了**x 为 1 的点。用 计算分母会导致除以零,这是一个未定义的条件,不是R 的成员元素,并且在代数闭包之外。y 在点 1,-1 处存在**间断性**(断裂) 并且没有解。在高级研究中,分别处理断裂点两侧变得非常重要。
计算分母会导致除以零,这是一个未定义的条件,不是R 的成员元素,并且在代数闭包之外。y 在点 1,-1 处存在**间断性**(断裂) 并且没有解。在高级研究中,分别处理断裂点两侧变得非常重要。

y 的其他线性形式可以通过一个**去除**其**间断性**的方程来表示。从 分子中提取因子
分子中提取因子 (使用**综合除法**)。
(使用**综合除法**)。


 (对于除 1 之外的所有 x) 。
(对于除 1 之外的所有 x) 。
将它的 (x-1) 个乘法逆元因子(倒数)约简到乘法单位元(1),保留了 因子(隐含的通用因子为 1/1)。限制这个简化函数的定义域;'除了
因子(隐含的通用因子为 1/1)。限制这个简化函数的定义域;'除了 之外的所有
之外的所有 ,其中x未定义',或者简单地'且 x ≠ 1'(意味着'且R2');使其等同于原函数。此表达式是 x 的线性函数,斜率 m = 2,y 截距纵坐标为 -3。表达式
,其中x未定义',或者简单地'且 x ≠ 1'(意味着'且R2');使其等同于原函数。此表达式是 x 的线性函数,斜率 m = 2,y 截距纵坐标为 -3。表达式 在 x = 1 处计算结果为 -1,但在该点函数 y 未定义(除以零)。函数 y 在 x = 1 处存在间断点。实际上,该函数在该点有一个类似于单点孔(跳跃)的间断,在图上显示为围绕该点的小空心圆。直线、射线和线段(以及弧、弦和曲线)用虚线或点线表示不连续。
在 x = 1 处计算结果为 -1,但在该点函数 y 未定义(除以零)。函数 y 在 x = 1 处存在间断点。实际上,该函数在该点有一个类似于单点孔(跳跃)的间断,在图上显示为围绕该点的小空心圆。直线、射线和线段(以及弧、弦和曲线)用虚线或点线表示不连续。
注意:非线性方程也可能是不连续的——参见后续的倒数函数 y = 1/x 的图形绘制,其中 y 不仅在一个点上,而且在沿 y 轴的“双”渐近线极值极点上是不连续的。当 x 在更小的幅度(- 和 +)上逼近零时,y 在函数的 - 和 + 映射中均趋于无定义。
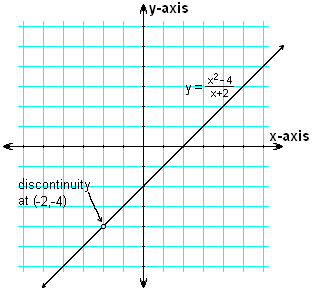
示例:以下函数的图形是什么样子的?

解答

将倒数 (x + 2) 因子约简到 1。这使得 y = x – 2 对所有 x 都成立,除了 x = -2,在该点存在间断点。直线 y = x – 2 的斜率 m = 1,y 截距纵坐标为 -2。因此,对于最终答案,我们绘制一条斜率为 1、y 截距为 -2 的直线,并在 x = -2 处显示一个间断点,否则 y 将等于 -4。
y-intercept ordinate of -2. So for the final answer , we graph a line with a slope of 1 and a y-intercept of -2, and we show a discontinuity at x = -2, where y would otherwise have been equal to -4.
示例:编写一个函数,其图形绘制的直线与 y = 2 x – 3 相同,但有两个间断点,一个在 x = 0 处,另一个在 x = 1 处。
解答:该函数必须有一个分母,其因子为
分母 = (x – 0)(x – 1) = x (x – 1) 。
在两个 x 值处具有“零点”。该函数的分子也获得保留整体因子 1 的因子,表达式相乘

__________例题结束__________
















































































































