微积分/连续性

定义连续性

现在我们准备好定义函数是**连续**的概念。这个想法是，我们想说一个函数是连续的，如果你可以在不抬起铅笔的情况下画出它的图形。但有时这对于图形的某些部分来说是正确的，而对于其他部分来说则不然。因此，我们想先定义函数在一个点上连续的含义。现在我们有了极限的概念，这个定义就简单了。

定义：（在一点处的连续性）

如果 $f(x)$ 在包含 $c$ 的一个开区间上定义，那么 $f(x)$ 被称为在**$c$ 处连续**当且仅当 $\lim _{x\to c}f(x)=f(c)$ 。

注意，对于 $f$ 在 $c$ 处连续，这个定义实际上要求三个条件

1. 即 $f$ 在 $c$ 处定义，因此 $f(c)$ 存在，
2. 当 $x$ 趋近于 $c$ 时，极限存在，并且
3. 极限和 $f(c)$ 相等。

如果这些条件中的任何一个不成立，那么 $f$ 在 $c$ 处不连续。

这个定义的意义是，对应于 $c$ 的图形点将接近对应于附近 $x$ 值的图形点。现在我们可以定义函数在一般情况下连续的含义，而不仅仅是在一个点上连续。

定义：（连续性）

如果一个函数在区间 $(a,b)$ 的每个点上都连续，那么称这个函数在 $(a,b)$ 上**连续**。

我们通常使用“函数是连续的”这句话来表示该函数在每个实数上都连续。这等同于说该函数在 $(-\infty ,\infty )$ 上连续，但简单地说“连续”更方便。

注意，根据我们已知的内容，只要有理函数、指数函数、三角函数或对数函数在某点定义，那么该函数在该点的极限值就等于其在该点的函数值。因此，所有这些函数在其定义域内都是连续的。（当然，它们在其未定义的地方不能是连续的！）

间断点

**间断点**是指函数不连续的点。当然，有很多可能导致这种情况发生的方式。在这里，我们只讨论两种简单的方式。

可去间断点

函数 $f(x)={\frac {x^{2}-9}{x-3}}$ 在 $x=3$ 处不连续。它在该点不连续，因为此时分数变为 ${\frac {0}{0}}$，这是未定义的。因此，该函数不满足我们在点 3 处连续性的三个条件中的第一个条件；3 根本不在其定义域内。

然而，我们说这种间断点是**可去**的。这是因为，如果我们在这个点修改函数，就可以消除间断点，使函数连续。为了了解如何使函数 $f(x)$ 连续，我们需要简化 $f(x)$，得到 $f(x)={\frac {x^{2}-9}{x-3}}={\frac {(x+3)(x-3)}{(x-3)}}={\frac {x+3}{1}}\cdot {\frac {x-3}{x-3}}$。我们可以定义一个新的函数 $g(x)$，其中 $g(x)=x+3$。注意，函数 $g(x)$ 与原始函数 $f(x)$ 不同，因为 $g(x)$ 在 $x=3$ 有定义，而 $f(x)$ 没有。因此，$g(x)$ 在 $x=3$ 是连续的，因为 $\lim _{x\to 3}(x+3)=6=g(3)$。但是，只要 $x\neq 3$，$f(x)=g(x)$；我们对 $f$ 做的只是使它在 $x=3$ 有定义。

事实上，这种简化对于有理函数的间断点来说通常是可能的。我们可以用公因数（在我们这个例子中是 $x-3$）来约分分子和分母，得到一个除了公因数为 0 的点（在我们这个例子中是 $x=3$）以外与原函数相同的函数。这个新函数将与旧函数相同，只是它在以前除以 0 的点被定义。

但是，并非所有情况下都可行。例如，函数 $f(x)={\frac {x-3}{x^{2}-6x+9}}$ 在分子和分母中都有一个公因子 $x-3$，但当您简化它时，会得到 $g(x)={\frac {1}{x-3}}$，它在 $x=3$ 处仍然没有定义。在这种情况下，$f(x)$ 和 $g(x)$ 的定义域相同，并且它们在其定义的每个地方都是相等的，因此它们实际上是同一个函数。原因是 $g(x)$ 与 $f(x)$ 在第一个例子中有所不同，是因为我们可以假设它有一个更大的定义域，而不是仅仅是定义 $f(x)$ 和 $g(x)$ 的公式不同。

跳跃间断

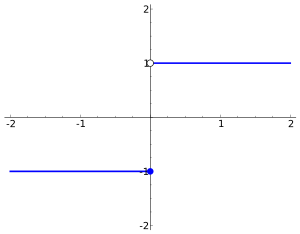
并非所有间断都可以从函数中去除。考虑这个函数

$k(x)={\begin{cases}1&{\text{if }}x>0\\-1&{\text{if }}x\leq 0\end{cases}}$

因为 $\lim _{x\to 0}k(x)$ 不存在，因此无法重新定义 $k$ 在一点处，使其在 0 处连续。这种间断被称为 *不可去除* 间断。

但是请注意，单边极限都存在；$\lim _{x\to 0^{-}}k(x)=-1$ 和 $\lim _{x\to 0^{+}}k(x)=1$。问题是它们不相等，因此图形在 0 的两侧之间“跳跃”。在这种情况下，我们说函数有一个 *跳跃* 间断。（注意，跳跃间断是一种不可去除的间断。）

单边连续

正如函数可以具有单边极限一样，函数也可以从特定的一侧连续。为了使函数在一点处从给定的一侧连续，我们需要满足以下三个条件

1. 该函数在该点处定义。
2. 该函数在该点处从该侧有一个极限。
3. 单边极限等于函数在该点处的值。

当且仅当函数在该点处从两侧都连续时，它才在该点处连续。现在我们可以定义函数在闭区间上连续的含义。

定义：（闭区间上的连续性）

当且仅当满足以下条件时，我们称一个函数在 $[a,b]$ 上 **连续**：

1. 它在 $(a,b)$ 上是连续的。
2. 它在 $a$ 处右连续。
3. 它在 $b$ 处左连续。

请注意，如果一个函数是连续的，那么它在其定义域内的每个闭区间上都是连续的。

介值定理

关于连续函数的一个有用定理如下

介值定理

如果一个函数 $f$ 在闭区间 $[a,b]$ 上是连续的，那么对于 $f(a)$ 和 $f(b)$ 之间的每个值 $y$ ，存在一个值 $c\in (a,b)$ 使得 $f(c)=y$ 。

应用：二分法

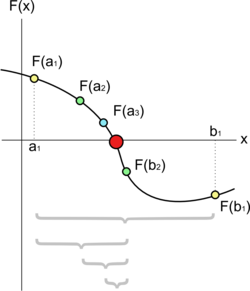在起始范围 $[a_{1},b_{1}]$ 上应用二分法的几个步骤。红色的大圆点是函数的根。

二分法是寻找连续函数零点的最简单、最可靠的算法。

假设我们要解方程 $f(x)=0$ 。给定两个点 $a$ 和 $b$ 使得 $f(a)$ 和 $f(b)$ 的符号相反，中间值定理告诉我们，只要 $f$ 在区间 $[a,b]$ 上是连续的，$f$ 必须在 $a$ 和 $b$ 之间至少有一个根。如果我们知道 $f$ 一般来说是连续的（例如，因为它由有理函数、三角函数、指数函数和对数函数组成），那么只要 $f$ 在 $a$ 和 $b$ 之间的每个点都被定义了，这将起作用。所以，让我们通过计算 $c={\frac {a+b}{2}}$ 将区间 $[a,b]$ 分为两半。现在有三种可能。

1. $f(c)=0$ ,
2. $f(a)$ 和 $f(c)$ 的符号相反，或者
3. $f(c)$ 和 $f(b)$ 的符号相反。

在第一种情况下，我们已经完成了。在第二和第三种情况下，我们可以对发生符号变化的子区间重复该过程。通过这种方式，我们将缩小到包含 0 的一个小子区间。小子区间的中间点通常被认为是 0 的一个很好的近似值。

请注意，与你在代数中学习到的方法不同，这种方法适用于你（或你的计算器）知道如何计算的任何连续函数。