微积分/积分技巧/三角代换
三角代换背后的想法很简单:用涉及标准三角函数的表达式替换涉及平方根的表达式,但不涉及平方根。涉及三角函数的积分通常比涉及平方根的积分更容易求解。
让我们在实践中演示这个想法。考虑表达式 。可能最基本的三角恒等式是 对于任意角度 。如果我们用 替换此表达式中的 ,借助这个三角恒等式,我们看到
注意我们可以写 因为我们用 替换了 。
需要指出的是,从技术角度而言,应该写出 的绝对值,换句话说,就是 作为最终答案,因为对于所有可能的 都有 。但是,只要我们对所有可能的 的定义域以及 在最终计算中的使用方式保持谨慎,省略绝对值符号并不会构成问题。但是,我们不能直接将简单的表达式 与复杂的 在任何地方互换,我们必须记住,在用换元法积分时,需要考虑导数。也就是说,我们需要记住 ,为了得到只包含 的积分,我们还需要用 来替换 。因此,如果我们看到一个形如
的积分,我们可以将其改写为
请注意左侧表达式中第一个 来自于替换 ,而 来自于用 替换。
由于 ,我们最初的积分简化为
- .
最后这两个积分很容易处理。对于第一个积分,我们得到
对于第二个积分,我们做一个替换,即 ,得到
最后我们看到
然而,这是以 为变量,而不是 ,所以我们必须代回去,才能用 重写答案。
也就是说,我们算出了
因此我们得到了最终答案
正如你所见,即使对于一个看起来相当简单的积分,这种方法也可能涉及到大量的计算。通常在使用三角代换之前,先看看是否可以用更简单的方法来求解是很有帮助的。另一方面,在涉及平方根的被积函数中,这通常是最有效的方法。首先,我们将给出一些经验规则来帮助你决定哪些三角代换可能会有所帮助。
如果被积函数包含以下形式的单个因子之一: 我们可以尝试三角代换。
- 如果被积函数包含 ,令 ,并使用恒等式 。
- 如果被积函数包含 ,令 ,并使用恒等式 。
- 如果被积函数包含 ,令 ,并使用恒等式 。


正弦代换
[edit | edit source]
如果被积函数包含形式为 的部分,我们使用以下代换
这将把被积函数转换为三角函数。如果新的被积函数无法直接积分,那么下面描述的半角正切代换通常会将它转换为一个更容易处理的代数被积函数。
例如,如果被积函数是,
如果被积函数是,我们可以将其改写为
然后我们可以进行以下替换
正切替换
[edit | edit source]
当被积函数包含形式的部分时,我们使用以下替换
例如,如果被积函数是 ,那么在进行这种代换后,我们发现
如果积分是
那么在进行这种代换后,我们发现
经过分部积分和使用三角恒等式后,我们得到了一个包含原始积分的表达式。在这种情况下,我们现在必须重新排列方程,以便原始积分仅出现在一边
正如我们从被积函数中预期的那样,当 很大时,它近似于 。
在某些情况下,即使积分中没有出现 ,也可以进行三角代换。
例如
该函数的分母等于 。这表明我们可以尝试用 代换,并使用恒等式 。用这种代换,我们得到 ,因此
使用初始替换 得到
正割代换
[edit | edit source]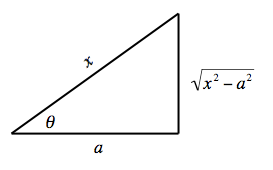
如果被积函数包含 形式的因子,我们使用以下替换
示例 1
[edit | edit source]求 。
求 .
现在我们可以用分部积分法
使用适当的三角代换求解以下积分。










































![{\displaystyle {\begin{aligned}\int \limits _{0}^{a}{\frac {1+x}{\sqrt {1-x^{2}}}}dx&=\int \limits _{0}^{\alpha }{\frac {1+\sin(\theta )}{\cos(\theta )}}\cos(\theta )d\theta &0<a<1\\&=\int \limits _{0}^{\alpha }{\bigl (}1+\sin(\theta ){\bigr )}d\theta &\alpha =\arcsin(a)\\&=\alpha +{\Big [}-\cos(\theta ){\Big ]}_{0}^{\alpha }\\&=\alpha +1-\cos(\alpha )\\&=1+\arcsin(a)-{\sqrt {1-a^{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d34bea926b8fc779d112222829c812acd2aa7561a)


![{\displaystyle {\begin{aligned}\int \limits _{0}^{z}(x^{2}+a^{2})^{-{\frac {3}{2}}}dx&=a^{-2}\int \limits _{0}^{\alpha }\cos(\theta )d\theta &z>0\\&=a^{-2}{\Big [}\sin(\theta ){\Big ]}_{0}^{\alpha }&\alpha =\arctan \left({\tfrac {z}{a}}\right)\\&=a^{-2}\sin(\alpha )\\&=a^{-2}{\frac {\frac {z}{a}}{\sqrt {1+{\frac {z^{2}}{a^{2}}}}}}\\&={\frac {z}{a^{2}{\sqrt {a^{2}+z^{2}}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4664e0be89a175f0c7b393341bd8ad28bbeb24c)

![{\displaystyle {\begin{matrix}I&=&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &&&\alpha =\tan ^{-1}(z/a)\\&=&a^{2}\int _{0}^{\alpha }\sec \theta \,d\tan \theta &&&\\&=&a^{2}[\sec \theta \tan \theta ]_{0}^{\alpha }&-&a^{2}\int _{0}^{\alpha }\sec \theta \tan ^{2}\theta \,d\theta &\\&=&a^{2}\sec \alpha \tan \alpha &-&a^{2}\int _{0}^{\alpha }\sec ^{3}\theta \,d\theta &+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\&=&a^{2}\sec \alpha \tan \alpha &-&I&+a^{2}\int _{0}^{\alpha }\sec \theta \,d\theta \\\end{matrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/313f2a452d4c096c9221cc6445317c894bb7eec0)


![{\displaystyle ={\tfrac {a^{2}}{2}}{\Bigg (}\sec(\alpha )\tan(\alpha )+{\bigg [}\ln {\Big (}\sec(\theta )+\tan(\theta ){\Big )}{\bigg ]}_{0}^{\alpha }{\Bigg )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09ca73ab74b8a68988b561b211957b826c9bcc9f)






















![{\displaystyle ={\bigg [}\tan(\theta )-\theta {\bigg ]}_{0}^{\alpha }\qquad \qquad \qquad \tan(\alpha )={\sqrt {\sec ^{2}(\alpha )-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eaf30ca894dfeaff2a765bb3ddb822a60753c656)





![{\displaystyle =-{\bigg [}\tan(\theta )\cos(\theta ){\bigg ]}_{0}^{\alpha }+\int \limits _{0}^{\alpha }\sec(\theta )d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/abddc762382184a13946dc8522620aa0ad23dff4)
![{\displaystyle =-\sin(\alpha )+{\bigg [}\ln {\bigl (}\sec(\theta )+\tan(\theta ){\bigr )}{\bigg ]}_{0}^{\alpha }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b45d861d862f65be50d6cf40c62770494cfa763)



