微积分/优化

简介

优化是微积分在现实世界中的应用之一。也许我们是一家比萨店，希望最大化利润。也许我们有一块平坦的硬纸板，我们需要用它制作体积最大的盒子。如何才能实现这个目标呢？

这需要用到最大值和最小值。我们知道，我们可以通过导数来找到最大值和最小值。因此，我们可以得出结论，微积分将成为最大化或最小化（统称为“优化”）某个情况的有用工具。

通常，优化问题有一个约束条件，它会改变我们看待问题的方式。问题的措辞（无论多么微妙）也会极大地改变我们看待问题的方式。约束条件是我们绝对不会改变的东西（例如，一般形状，或者我们愿意为整个操作支付的金额等等）。如果我们能够识别出我们将要改变什么以及我们将要求保持不变的东西，那么我们就将开始解决问题。

如何解决

为了完成优化问题，应该按照以下步骤进行。

1. 写出问题中给出的必要公式和其他信息。
   • 问题应该有一个你可以控制的变量和一个你想要最大化/最小化的变量。
   • 你找到的公式可能包含额外的变量。根据问题的解决方式，这些变量可能会被替换掉，或者可以忽略（稍后将进行解释）。
2. 将公式组合起来，使你想要最大化/最小化的变量位于等式的左侧，所有其他变量位于右侧。
3. 对公式求导。如果你的方程包含多个变量，可以选择任何变量进行求导，只要它不是你控制的变量（即，选择你无法从公式中消除的变量）。
   • 请注意，在求导过程中，如果你遇到一个你没有选择的变量，将其视为一个数字并应用必要的求导规则。在这种情况下，不要将其视为变量。
4. 将求导后的公式设为 0，并求解你控制的变量。
5. 你在这里得到的值就是你的答案。如果你得到另一个公式，这意味着你的答案取决于其他变量，这通常是你最初遇到这种情况时，问题所要求的。

这种算法之所以有效，是因为几个数学定理，而这些定理你可能在解决这些问题时并不需要知道。通常给出的问题在数学上都很简单（换句话说，没有很多情况需要测试）。但是，如果你想了解，它们是这样的

• 导数为 0 的点，要么是全局最大值或最小值，要么是局部最大值或最小值。通常问题会倾向于在没有太多困难的情况下回答这个问题（例如，总是正数）。

示例

体积示例

一个盒子制造商想要制作一个表面积为 100 平方英寸的封闭盒子，该盒子具有正方形底座，但侧面为矩形。将这种材料弯成盒子后，可以形成的最大体积是多少？

• 写出已知的公式和信息

$A_{base}=x^{2}$

$A_{side}=x\cdot h$

$A_{total}=2x^{2}+4x\cdot h=100$

$V=l\cdot w\cdot h=x^{2}\cdot h$

• 将变量 $h$ 写成体积方程中 $x$ 的表达式。

$2x^{2}+4xh=100$

$x^{2}+2xh=50$

$2xh=50-x^{2}$

$h={\frac {50-x^{2}}{2x}}$

${\begin{aligned}V&=\left(x^{2}\right)\left({\frac {50-x^{2}}{2x}}\right)\\&={\frac {50x-x^{3}}{2}}\end{aligned}}$

• 为了最大化体积，求体积方程的导数

${\frac {dV}{dx}}={\frac {50-3x^{2}}{2}}$

• 令${\frac {dV}{dx}}=0$，并解出$x$

${\frac {50-3x^{2}}{2}}=0$

$50-3x^{2}=0$

$3x^{2}=50$

$x=\pm {\frac {\sqrt {50}}{\sqrt {3}}}$

• 将$x$值代入体积方程并化简

${\begin{aligned}V&={\frac {1}{2}}\left[50{\sqrt {\frac {50}{3}}}-\left({\sqrt {\frac {50}{3}}}\right)^{3}\right]\\&=68.04138174...\end{aligned}}$

答案：$V_{max}=68.04138174...$

体积示例二

想要用一块边长为$\alpha$的正方形锡片制作一个最大容积的无盖箱子，方法是在角上剪去相同的正方形，然后折起锡片形成箱子的侧面。剪去的正方形的边长应该为多少？

如果我们将切口正方形的边长称为$x$，那么折叠盒底部的每条边都是$\alpha -2x$，高度是$x$。因此，体积函数是$V(x)=x(\alpha -2x)^{2}=x(\alpha ^{2}-4\alpha x+4x^{2})=\alpha ^{2}x-4\alpha x^{2}+4x^{3}$。我们必须通过对体积函数求导并将其设置为0来优化体积。由于它不改变，$\alpha$被视为常数，而不是变量。

$V(x)=\alpha ^{2}x-4\alpha x^{2}+4x^{3}$

${\begin{aligned}0&=V'(x)=\alpha ^{2}-8\alpha x+12x^{2}\\&=12x^{2}-8\alpha x+\alpha ^{2}\end{aligned}}$

现在我们可以使用二次公式来求解$x$

$x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}$

${\begin{aligned}x&={\frac {-(-8\alpha )\pm {\sqrt {(-8\alpha )^{2}-4(12)(\alpha ^{2})}}}{2(12)}}\\&={\frac {8\alpha \pm {\sqrt {64\alpha ^{2}-48\alpha ^{2}}}}{24}}\\&={\frac {8\alpha \pm {\sqrt {16\alpha ^{2}}}}{24}}\\&={\frac {8\alpha \pm 4\alpha }{24}}\end{aligned}}$

$x={\frac {\alpha }{6}},{\frac {\alpha }{2}}$

我们拒绝$x={\frac {\alpha }{2}}$，因为它是最小值（它会导致底边长度$\alpha -2x$为0，使体积为0）。

因此，答案是$x={\frac {\alpha }{6}}$。

体积示例 III

需要一个圆柱形罐子来盛放$1.024{\text{ L}}$ 的液体。确定能使制造指定体积罐子所需的材料量最小的尺寸。

这是一个经典的优化问题。问题是我们没有任何指定的尺寸。幸运的是，我们给出了国际单位制，因此我们可以相应地写出我们给出的内容。

• 转换因子：$1{\text{ L}}=1000{\text{ cm}}^{3}$。这意味着通过量纲分析（或基本代数）：$1.024{\text{ L}}=1024{\text{ cm}}^{3}$。请记住，这是体积！
• 圆柱体积：$V=\pi r^{2}h$
• 圆柱表面积：$S=2\pi rh+2\pi r^{2}$

请记住我们要最小化什么：“制造指定体积罐子所需的材料量”。这意味着表面积需要最小化！不幸的是，我们有两个变量（它不是常数）。幸运的是，我们可以使用体积来写$h$ 关于$r$ 的表达式。

$1024{\text{ cm}}^{3}=\pi r^{2}h$

$\Rightarrow {\frac {1024{\text{ cm}}^{3}}{\pi {r{\text{ cm}}}^{2}}}={\frac {1024}{\pi r^{2}}}{\text{ cm}}=h$

我们可以将此信息代入表面积公式并最小化（将一阶导数设为零）

$S(r)=2\pi r\left({\frac {1024}{\pi r^{2}}}\right)+2\pi r^{2}$。消除$\pi$ 和$r$。

$\Rightarrow S(r)=2\cdot {\frac {1024}{r}}+2\pi r^{2}$ 将一阶导数设为零。

${\begin{aligned}\Rightarrow 0=S'(r)&={\frac {d}{dr}}\left({\frac {2048}{r}}+2\pi r^{2}\right)\\&={\frac {d}{dr}}\left({\frac {2048}{r}}\right)+{\frac {d}{dr}}\left(2\pi r^{2}\right)\\&={\frac {d}{dr}}\left(2048\cdot {r}^{-1}\right)+2\pi {\frac {d}{dr}}\left(r^{2}\right)\\&=2048\cdot {\frac {d}{dr}}\left({r}^{-1}\right)+2\pi \left(2r\right)\\&=2048\cdot (-1){r}^{-2}+4\pi r\\&=-{\frac {2048}{{r}^{2}}}+4\pi r\\&={\frac {4\pi r^{3}-2048}{{r}^{2}}}\end{aligned}}$

接下来要做的就是找到操作的临界值。 这最终意味着让分子等于零，并找到什么值 $r$ 使分母等于零。 这是分子运算

$4\pi r^{3}-2048=0$

$\Leftrightarrow 4\pi r^{3}=2048$

$\Leftrightarrow r^{3}={\frac {2048}{4\pi }}={\frac {512}{\pi }}$

$\Leftrightarrow r={\sqrt[{3}]{\frac {512}{\pi }}}={\frac {8}{\sqrt[{3}]{\pi }}}\approx 5.4623$

这是分母的运算

${r}^{2}=0$

$r=\pm 0$

需要注意的是，我们并不关心其中一个临界值是否等于零。这个问题要求我们找到使条件成立且最小化的值。虽然零确实最小化了建造罐头所需的材料量，但如果我们不显示一个罐头，我们就无法建造罐头。然而，如果我们被问及 $S(r)$ 的图形，这个解就会很有趣。尽管如此，我们的最终答案不一定就是 $r\approx 5.4623{\text{ cm}}$ 和 $h\approx 10.9245{\text{ cm}}$。我们需要验证我们找到的临界值是否为正确答案。这时，我们需要将 $r\in \left(0,\,{\frac {8}{\sqrt[{3}]{\pi }}}\right)$ 和 $r\in \left({\frac {8}{\sqrt[{3}]{\pi }}},\,\infty \right)$ 的值代入一阶导数。

对于 $r\in \left(0,\,{\frac {8}{\sqrt[{3}]{\pi }}}\right)$，令 $r=5$：$S'(5)={\frac {4\pi (5)^{3}-2048}{(5)^{2}}}<0$。对于 $r\in \left({\frac {8}{\sqrt[{3}]{\pi }}},\,\infty \right)$，令 $r=6$：$S'(6)={\frac {4\pi (6)^{3}-2048}{(6)^{2}}}>0$。

根据以上结果，很明显 $r={\frac {8}{\sqrt[{3}]{\pi }}}$ 是一个最小化函数的值，同时允许我们建造罐头。请记住，如果你没有证明我们找到的值是极小值，那么这个值也可能是极大值。想象一下，如果情况是这样的，我们建议公司生产一个最大化材料用量的罐头。潜在的数百万美元的材料成本将抵消最佳利润。无论哪种情况，我们都找到了答案。

答案：半径为 $5.4623{\text{ cm}}$，高度为 $10.9245{\text{ cm}}$。

销售示例

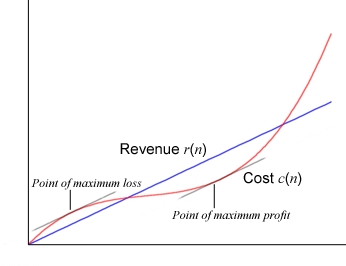
一家小型零售商可以以 $n$ 的数量售出一件产品，其收入为 $r(n)=8.1n$，成本为 $c(n)=n^{3}-7n^{2}+18n$，所有金额均以千计。它需要售出多少单位才能使其利润最大化？

零售商的利润由等式 $p(n)=r(n)-c(n)$ 定义，它表示产生的净收入。问题要求利润最大化，或者上述等式的最大值。如前所述，图形的最大值和最小值是在图形的斜率等于零时找到的。要找到斜率，需要找到感兴趣的函数的导数——这里，$p(n)$。利用减法法则 $p'(n)=r'(n)-c'(n)$

$p(n)=r(n)-c(n)$

$p'(n)={\frac {d}{dn}}[8.1n]-{\frac {d}{dn}}\left[n^{3}-7n^{2}+18n\right]=-3n^{2}+14n-9.9$

因此，当 $-3n^{2}+14n-9.9=0$ 时，利润将被最大化或最小化。使用 二次公式 求解根，得到 $n=0.869,3.798$。要找到这两个中的哪一个是最大值和最小值，可以对函数进行测试

$p(0.869)=-3.97321,p(3.798)=8.58802$

因为我们只考虑所有 $n\geq 0$ 的函数（即，你不可能有 $n=-5$ 个单位），唯一可能成为最小值或最大值的点是上面列出的这两个点。为了证明 $3.798$ 实际上是一个最大值（以及该函数在这一点之后不保持恒定），检查 $p'(n)$ 的符号在这一点上是否发生变化。

在这里，它确实如此，并且对于大于$3.798$的$n$，$P'(n)$ 将继续下降。这表明公司将在$n=3.798$ 处实现利润最大化。销售$3.798$ 个单位的零售商将获得 $$8,588.02$ 的利润。

然而，答案是$n=3.798$.

收入示例

最大化收入

一家小部件公司具有线性需求函数 $D(q)=-{\frac {1}{5}}q+10$，其中 $q$ 是运送给客户的小部件（以百计）的公斤数。小部件应该以什么价格出售才能使收入最大化？

公司的收入是通过将销售数量乘以价格来计算的。由于$D(q)$ 是价格，而 $q$ 是销售数量，$R(q)=q\cdot D(q)$。问题要求我们找到将数量最大化的价格。这意味着找到数量是第一个目标。最终目标是找到的价格。

我们的第一个目标是找到使收入最大化的数量。如果切线的斜率在某一点为零，并且该点周围斜率的符号从正变为负，则收入函数将被最大化。这是通过求导数并应用一阶导数检验来实现的。当收入函数分配$q$ 时，这将更容易

${\begin{aligned}R(q)&=q\cdot D(q)\\&=q\cdot \left(-{\frac {1}{5}}q+10\right)\\&=-{\frac {1}{5}}q^{2}+10q\end{aligned}}$

现在让我们求一阶导数

${\frac {d}{dq}}\left[R(q)\right]={\frac {d}{dq}}\left[-{\frac {1}{5}}q^{2}+10q\right]$

${\begin{aligned}R'(q)&={\frac {d}{dq}}\left[-{\frac {1}{5}}q^{2}\right]+{\frac {d}{dq}}\left[10q\right]\\&=-{\frac {1}{5}}{\frac {d}{dq}}\left[q^{2}\right]+10{\frac {d}{dq}}\left[q\right]\\&=-{\frac {1}{5}}\left[2q\right]+10\left[1\right]\\&=-{\frac {2}{5}}q+10\end{aligned}}$

将一阶导数设为零以找到临界值

$R'(q)=0=-{\frac {2}{5}}q+10$

$\Leftrightarrow -10=-{\frac {2}{5}}q$

$\Leftrightarrow 25=q$

请注意原始的收入函数。因为收入函数是一个二次函数，其 $q^{2}$ 项乘以小于 0 的因子，因此保证只有一个临界值，并且它必须是最大值。基于微积分的方法只是证实了这一事实（使用一阶导数检验）

对于任何 $q<25$，$R'(q)>0$。对于任何 $q>25$，$R'(q)<0$。因此，临界值 $q=25$ 必须是最大值。

剩下的就是将这个域输入到需求函数中，以找到小部件的售价。这是一个简单的替换练习

${\begin{aligned}D(25)&=-{\frac {1}{5}}(25)+10\\&=-5+10\\&=5\end{aligned}}$

小部件应该以 $$5$ 的价格出售以使收入最大化。

函数到原点的距离

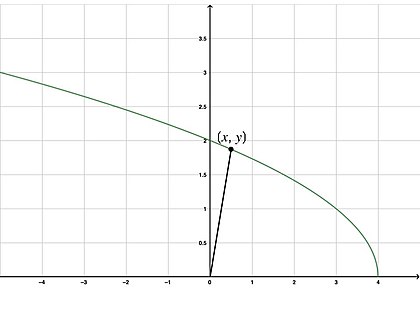
一个典型的优化问题，尽管有点抽象。

函数 $f(x)={\sqrt {4-x}}$ 在 $xy$ 平面上绘制。函数上的一个粒子应该停在函数的哪个点，使得该点到原点的直线距离最小化？

让我们写下所有可能需要记住的相关方程

• $D={\sqrt {\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}}}$
• $y=f(x)$

优化问题的一个难点在于，大多数情况下我们处理的是两个变量而不是一个变量。然而，主要思路和重点是将二元方程转化为一元方程。这里需要将变量联系起来。最好的方法是利用问题的设置来发挥优势。

我们希望将函数保留在 $(x,y)$，并最小化到达原点的距离。这意味着我们设 $\left(x_{2},y_{2}\right)=(x,y)$。回顾一下，原点位于 $(0,0)$，所以 $\left(x_{1},y_{1}\right)=(0,0)$。有了这里的所有信息，让我们用单变量 $x$ 来写出距离函数。因为 $y=f(x)$

${\begin{aligned}D(x)&={\sqrt {\left(x-0\right)^{2}+\left(f(x)-0\right)^{2}}}\\&={\sqrt {x^{2}+\left({\sqrt {4-x}}\right)^{2}}}\\&={\sqrt {x^{2}+4-x}}\\&={\sqrt {x^{2}-x+4}}\end{aligned}}$

我们将展示两种求导方法：标准方法和非标准方法。标准方法需要使用链式法则，让我们演示一下这个过程。

标准方法

$D(x)={\sqrt {x^{2}-x+4}}$

$\Rightarrow {\frac {d}{dx}}\left[D(x)\right]={\frac {d}{dx}}\left({\sqrt {x^{2}-x+4}}\right)$

${\begin{aligned}\Rightarrow D'(x)&={\frac {d}{dx}}\left({\sqrt {x^{2}-x+4}}\right)&\left({\text{Recall the chain rule: }}{\frac {d}{dx}}\left[f\left(g(x)\right)\right]={\frac {df}{dg}}\cdot {\frac {dg}{dx}}\right)\\&={\frac {d}{dx}}\left(x^{2}-x+4\right)\cdot {\frac {df}{dg}}\left({\sqrt {x^{2}-x+4}}\right)\\&=\left(2x-1\right)\cdot {\frac {1}{2{\sqrt {x^{2}-x+4}}}}\\&={\frac {2x-1}{2{\sqrt {x^{2}-x+4}}}}\end{aligned}}$

现在我们有了距离公式的一阶导数。为了最小化 $(x,y)$ 与原点之间的距离，我们将一阶导数设为零。到目前为止，你应该知道为什么要这样做。

令 $D'(x)=0$.

${\frac {2x-1}{2{\sqrt {x^{2}-x+4}}}}=0$ 意味着分子为零。因此

令 $2x-1=0$.

$2x-1=0$

$\Leftrightarrow 2x=1$

$\Leftrightarrow x={\frac {1}{2}}$

回想一下，如果分母可以被设为零，那么使之成立的 $x$ 值是一个临界值。因此，令 $2{\sqrt {x^{2}-x+4}}=0$

$2{\sqrt {x^{2}-x+4}}=0$

$\Rightarrow {\sqrt {x^{2}-x+4}}=0$

$\Rightarrow x^{2}-x+4=0$

对于 $x$，不存在任何使上述方程成立的实际值。这可以通过行列式小于零来证明：$b^{2}-4ac<0$。因此，

唯一的临界值为 $x={\frac {1}{2}}$。现在，你应该会想到我们需要使用一阶导数测试

对于任何 $x<{\frac {1}{2}}$，$D'(x)<0$。对于任何 $x>{\frac {1}{2}}$，$D'(x)>0$。这意味着临界值之前的函数在递减，临界值之后的函数在递增。这说明临界值处的函数为局部最小值。

因此，$x$的值将使 $(x,y)$ 与原点之间的距离最小，值为 $x={\frac {1}{2}}$。

然而，你还没有完成这个问题。你还需要找到粒子需要停止的函数点。这只是将 $x$ 代入函数 $f(x)$ 的问题。

${\begin{aligned}f\left({\frac {1}{2}}\right)&={\sqrt {4-\left({\frac {1}{2}}\right)}}\\&={\sqrt {{\frac {8}{2}}-{\frac {1}{2}}}}\\&={\sqrt {\frac {7}{2}}}\end{aligned}}$

大多数微积分课程的老师并不介意你将答案保留为 $\left({\frac {1}{2}},{\sqrt {\frac {7}{2}}}\right)$。然而，对于少数关心分母有理化的老师或考试机构，${\sqrt {\frac {7}{2}}}$ 的工作如下

${\begin{aligned}{\sqrt {\frac {7}{2}}}&={\frac {\sqrt {7}}{\sqrt {2}}}\\&={\frac {\sqrt {7}}{\sqrt {2}}}\cdot {\frac {\sqrt {2}}{\sqrt {2}}}\\&={\frac {{\sqrt {7}}\cdot {\sqrt {2}}}{2}}\\&={\frac {\sqrt {14}}{2}}\\\end{aligned}}$

这就是为什么大多数老师不介意分母保留为平方根的原因；它会分散对微积分的注意力（虽然只是略微分散）。这让我们得到了最终答案

为了使粒子到达原点的距离最小，粒子必须在 $\left({\frac {1}{2}},{\frac {\sqrt {14}}{2}}\right)$ 离开函数。 $\blacksquare$

非标准方法：隐式微分

由于除了隐式微分之外的任何计算都会导致与之前概述的相同过程，因此这里只展示隐式微分。回想一下 $D(x)={\sqrt {x^{2}-x+4}}$。将两边平方得到以下函数

$\left[D(x)\right]^{2}=x^{2}-x+4$

对上述函数关于 $x$ 求导需要我们进行隐式微分（尽管这种微分被巧妙地掩盖了）。下面的计算展示了这一过程

${\frac {d}{dx}}\left[\left(D(x)\right)^{2}\right]={\frac {d}{dx}}\left(x^{2}-x+4\right)$

${\begin{aligned}\Rightarrow 2D(x){\frac {dD}{dx}}&={\frac {d}{dx}}\left(x^{2}\right)-{\frac {d}{dx}}\left(x\right)+{\frac {d}{dx}}\left(4\right)\\&=2x-1+0\\\end{aligned}}$

$2D(x){\frac {dD}{dx}}=2x-1$

${\begin{aligned}\Leftrightarrow {\frac {dD}{dx}}&={\frac {2x-1}{2D(x)}}\\&={\frac {2x-1}{2{\sqrt {x^{2}-x+4}}}}\end{aligned}}$

请注意，上面的计算得出的结果与用标准方法求出的第一个导数相同，这意味着从这里开始的计算将是相同的。有了这个，让我们进入下一个问题。

最大化弯曲架子形成的矩形区域

这里的问题是另一个问题的伪装变体。

假设有一个函数 $f(x)=15\log(x)$ 描述了一个风格化货架一部分的曲线。这条曲线在距离垂直墙壁水平方向 $100$ 厘米处结束。制造商希望这部分货架的前表面有一个大的矩形凹槽，凹槽的左上角形成一个与货架底部平行的水平部分。为了满足制造商的要求，这个凹槽所形成的垂直墙壁距离货架左侧多远？可以使用计算器进行计算。

这个问题看起来很奇怪。但实际上，这是一个经过伪装的常见优化问题变种，即函数问题中形成的最大矩形区域。如果用这种思路来考虑问题，问题会变得更容易处理。毕竟，制造商想要的是最大化凹槽尺寸。他没有询问尺寸的体积，只是询问在哪里可以找到满足要求的部分。

右侧所示的图像实际上就是所形成的最大区域。然而，如果问题没有提供图像（以及轴上的数字），那么就无法进行近似。

令 $x$ 表示距离货架左侧的距离，令所形成的矩形的高度为 $y=f(x)$。这种构造意味着 $(100-x)$ 是矩形的长度，而高度是 $15\log(x)$。因此，面积函数为

$A(x)=15(100-x)\log(x)$

我们要找到该函数的最大值。让我们求出面积函数的导数并令其等于零

$A(x)=15(100-x)\log(x)$

$\Rightarrow {\frac {d}{dx}}\left[A(x)\right]={\frac {d}{dx}}\left[15(100-x)\log(x)\right]$

${\begin{aligned}\Rightarrow A'(x)&=15{\frac {d}{dx}}\left((100-x)\log(x)\right)&\left({\text{Recall the product rule: }}{\frac {d}{dx}}\left[f(x)\cdot g(x)\right]=f\cdot {\frac {dg}{dx}}+g\cdot {\frac {df}{dx}}\right)\\&=15\left[(100-x)\cdot {\frac {d}{dx}}\left(\log(x)\right)+\log(x)\cdot {\frac {d}{dx}}\left(100-x\right)\right]\\&=15\left[{\frac {100-x}{x\ln(10)}}-\log(x)\right]\\&=15\left[{\frac {100-x}{x\ln(10)}}-{\frac {\ln(x)}{\ln(10)}}\right]&\left({\text{Multiply by }}{\frac {x}{x}}{\text{ to the right fraction.}}\right)\\&=15\left[{\frac {100-x}{x\ln(10)}}-{\frac {x\ln(x)}{x\ln(10)}}\right]\\&=15\left[{\frac {100-x-x\ln(x)}{x\ln(10)}}\right]=0\\\end{aligned}}$

然而，在找到一阶导数后，很明显，我们目前还不知道在这种特定情况下如何求解 $x$ 的值，因为我们还不知道 Lambert-W 函数。因此，现在可以使用图形计算器（通常，许多老师希望在允许你使用计算器求解之前看到尽可能多的步骤）。如果没有图形计算器，可以使用 Desmos 或 Geogebra 或其他许多在线图形计算器。

这些网站获得的答案是 $x\approx 23.94721$ 或精确解 $x=e^{W(100e)-1}$。我们知道这也是我们正在寻找的最大值，因为导数函数在 $x<23.94721$ 时为正，但在之后变为负。对于那些好奇的人来说，最大面积是 $1573.44277$ 平方厘米。

答案：$x\approx 23.94721$

不同区域的速度

我们试图找到的示意图：到达目的地所需的最短距离 $\Lambda$。

根据费马最小时间原理，光线以最短时间跨越最短距离（即，光线以最少浪费时间的方式传播）。光波的速度定义为光速除以传播介质的折射率，即 $v={\frac {c}{n}}$。假设一束光波穿过两种材料，从 $n_{1}$ 开始，在 $n_{2}$ 结束，其中 $n_{1}<n_{2}$。入射角和折射角在右边的图中给出。光线穿过两种不同材料之间的关系是什么？

这看起来不像一个优化问题。实际上，看起来尝试将其变成一个优化问题会不合常理。然而，这个物理学中的漂亮结果仅仅是通过将其变成一个优化问题而发现的巧妙发现。

让我们写下我们所知道的

• 入射点和材料变化之间的距离是 $\Upsilon$（图中使用的是斜体大写的upsilon）。
• 使传播时间最短的距离是 $\Lambda$（图中使用的是斜体大写的lambda）。这意味着根据图示，剩余的水平距离是 $d-\Lambda$。
• 材料变化和折射材料末端之间的距离是 $\Gamma$（图中使用的是斜体大写的gamma）。

剩下的就是把所有东西拼凑起来了。我们想要找到光线传播的距离。

• 入射光线传播的距离是 ${\sqrt {(\Lambda )^{2}+(\Upsilon )^{2}}}$.
• 折射光线传播的距离是 ${\sqrt {(d-\Lambda )^{2}+(\Gamma )^{2}}}$.

让我们回顾一下我们所知道的。我们试图操作 $\Lambda$ 使得传播时间尽可能短，从而反映和模拟光线穿过两种不同材料的方式。除 $\Lambda$ 以外的所有其他非函数项都是常数。由于我们试图模拟光线穿过两种不同材料所需的时间，因此我们应该操作距离使其模拟时间。

回想一下，速度是距离和时间的比值 $\left(v={\frac {D}{\Delta t}}\right)$，因此使用给定距离模拟光线传播所需的时间，只需要进行一些重新排列即可。由于光线穿过两种不同的材料，速度不同。设 $v_{1}>v_{2}$，其中 $v_{1}$ 是光线在折射率为 $n_{1}$ 的第一种材料中传播的速度（$v_{2}$ 也是如此）。

• $t_{1}={\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}$
• $t_{2}={\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}$

光线穿过这两种材料所需的时间以 $\Lambda$ 的函数形式给出，因此

• $T(\Lambda )=t_{1}+t_{2}={\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}+{\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}$

现在我们终于有了优化问题。我们想要最小化传播时间。将 $T(\Lambda )$ 的一阶导数设为零。记住，除了 $\Lambda$ 以外的所有其他项都是常数。

$T(\Lambda )={\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}+{\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}$

${\frac {d}{d\Lambda }}\left[T(\Lambda )\right]={\frac {d}{d\Lambda }}\left({\frac {\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}{v_{1}}}+{\frac {\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}{v_{2}}}\right)$

回顾我们想要解决的问题。我们不是要解出$\Lambda$；我们试图对情况进行建模。如果我们确实需要解出$\Lambda$，那将是一场噩梦（我们甚至可以将其留作读者的一个非平凡练习），但无论如何，我们可以开始对情况进行建模。首先，将负项移到另一边

${\frac {1}{v_{1}}}\cdot \left({\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}\right)-{\frac {1}{v_{2}}}\cdot \left({\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}\right)=0$

${\frac {1}{v_{1}}}\cdot \left({\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}\right)={\frac {1}{v_{2}}}\cdot \left({\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}\right)$

该图显示了应用不同几何特性后涉及的角度之间的关系。

接下来我们应该尝试重写表达式，以便清理那些分数（毕竟它们很吓人，而且建模也不实用）。

我们可以在这里使用三角函数来帮助我们。因为三角函数只是直角三角形比率的关系，所以这将是一个非常好的解决方案。

法线被定义为垂直于给定“表面”的线。由于距离$\Upsilon$平行于法线，因此它所产生的角度也是$90^{\circ }$。由于光传播的水平距离$d$平行于“表面”，因此光线的入射角$\theta _{1}$，是距离$\Upsilon$和入射光矢量$\mathbf {I}$之间的角度，并且光矢量$\mathbf {I}$是横截线，根据同位角定理，距离$\Upsilon$和入射光矢量$\mathbf {I}$之间的角度也是$\theta _{1}$（参见图的左上角以供参考）。

这种几何推导的结果很简单：我们找到了直角三角形的一部分的角度。因此，我们可以将距离写成三角函数的等价形式

• $\sin(\theta _{1})={\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}$

我们可以用类似的逻辑来证明

• $\sin(\theta _{2})={\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}$

因此，我们可以将相关的方程式改写成更易于管理和计算的形式，而无需测量比率。

${\frac {1}{v_{1}}}\cdot \left({\frac {\Lambda }{\sqrt {\Lambda ^{2}+\Upsilon ^{2}}}}\right)={\frac {1}{v_{2}}}\cdot \left({\frac {d-\Lambda }{\sqrt {(d-\Lambda )^{2}+\Gamma ^{2}}}}\right)$

$\Leftrightarrow {\frac {1}{v_{1}}}\cdot \sin(\theta _{1})={\frac {1}{v_{2}}}\sin(\theta _{2})$

我们实际上还没有解决这个问题。尽管我们可能已经将两个不同的光向量联系起来，但我们并没有根据折射率对这种情况进行建模。这留下了最后两个步骤。回顾一下，光线穿过折射率为 $n$ 的特定材料的速度为 $v={\frac {c}{n}}$。这等同于说 ${\frac {1}{v}}={\frac {n}{c}}$。由于速度与折射率有关，我们可以将上面的方程式改写为

${\frac {n_{1}\cdot \sin(\theta _{1})}{c}}={\frac {n_{2}\cdot \sin(\theta _{2})}{c}}$

两边都乘以 $c$，我们终于找到了 *斯涅尔定律*

答案：$n_{1}\sin(\theta _{1})=n_{2}\sin(\theta _{2})$

请记住，这个结果仍然是一个导数。但是，我们允许根据微分方程对现实生活中的场景进行建模。有时，可能无法在没有微分方程的情况下对情况进行建模。我们允许这样写我们的方程（物理学当然不在乎这里）。最后，虽然这不是严格意义上的优化问题，但从这个角度思考使我们能够获得一个关于世界的良好规则（科学中的 *定律*）。我们证明了这种行为，所以光似乎将根据这个方程保持一致。实际上，这使我们能够在 2003 年确认负折射率的存在（即使通过实验观察），并使我们能够发现自旋波的性质。