电路理论/卷积积分/示例/example49

串联 LRC 电路... 找出电阻两端的电压

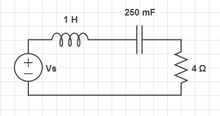
已知电源电压为 (2t-3t²)，求电阻两端的电压。

可以专注于 V_r 或者：电流，V_c，或 V_L，然后转换为 V_r.. 以下是 V_R 的解。

概要

传递函数

$H(s)={\frac {V_{R}}{V_{S}}}={\frac {4}{4+s+{\frac {1}{0.25s}}}}$

simplify(4/(4 + s + 1/(0.25*s)))

$H(s)={\frac {4s}{s^{2}+4s+4}}$

齐次解

solve(s^2 + 4.0*s + 4.0,s)

在 s = -2 处有两个相等的根，所以解的形式为

$V_{R_{h}}(t)=Ae^{-2t}+Bte^{-2t}+C_{1}$

特解

在长时间连接到一个单位阶跃函数源之后，电感器短路，电容器开路。所有电压降落在电容器上。电流为零。

$V{R_{p}}=0$

这也意味着 C₁ 必须为零。

初始条件

到目前为止，完整的方程是

$V_{R}(t)=Ae^{-2t}+Bte^{-2t}$

由于假设的电感器的初始条件，串联支路的初始电流为零。这意味着 V_R = 0

$V_{R}(0)=0=A$

$A=0$

假设电容器上的初始电压为零，则没有电流流动，因此电阻上的压降为零。

$i(t)={\frac {V_{R}}{4}}$

$V_{L}(t)=L{di(t) \over dt}={\frac {1}{4}}((-2A+B)e^{-2t}-2Bte^{-2t})$

$V_{L}(0)=1={\frac {B}{4}}$

$B=4$

$V_{R}(t)=4te^{-2t}$

脉冲解

对上面求导得到

$V_{R}\delta (t)=4e^{-2t}-8te^{-2t}$

卷积积分

$V_{R}(t)=\int _{0}^{t}(4e^{-2(t-x)}-8(t-x)e^{-2(t-x)})(2x-3x^{2})dx$

f := (4*exp(-2*(t-x)) - 8*(t-x)exp(-2*(t-x)))*(2*x-3*x^2);
S :=int(f,x=0..t)

$V_{R}(t)=8-8e^{-2t}-10te^{-2t}-6t$

由于V_R(t)在长时间后等于0，并且电容打开，所以这里不会有常数项。