电路理论/相量/示例/示例 7

示例 7 的串联 RL 电路

已知电压源由 $V_{s}(t)=120{\sqrt {2}}cos(377t+120^{\circ })$ 定义，求所有其他电压、电流并检查功率。

标注回路和节点

标记用于分析的串联 RL 电路

重要的是，即使源在振荡，也不会有任何变化。+ 和 - 仍然必须捕捉电路拓扑并融入方程。

关于这个问题值得注意的是，它正在谈论一个墙上插座。

角频率 377 $\omega$ 是 60 Hz $f$

$f={\frac {\omega }{2\pi }}={\frac {377}{2\pi }}=60$

The $V_{RMS}={\frac {V_{peak}}{\sqrt {2}}}$ so $V_{peak}=V_{RMS}*{\sqrt {2}}$，因此，该问题的大小与北美标准的 120 伏特 rms 墙上插座相匹配。

已知量、未知量和方程

已知量：$V_{s},R,L$

未知量：$i,v_{R},v_{L}$

方程：$v_{R}(t)=R*i(t),v_{L}=L*{d \over dt}i(t),v_{R}(t)+v_{L}(t)-V_{s}(t)=0$

相量符号

时域

将端点方程代入回路方程得到：

$R*i(t)+L*{d \over dt}i(t)-V_{s}(t)=0$

假设 ${V_{s}}$ 可以写成 $\operatorname {Re} (V_{m}e^{j(\omega t+\phi )})$

相量域

现在将方程变换到相量域..

${V_{s}}(t)\rightarrow {\mathbb {V} _{s}}=V_{m}\angle \phi$

$i(t)\rightarrow \mathbb {I}$

${d \over dt}i(t)\rightarrow j\omega \mathbb {I}$

所以

$R*\mathbb {I} +L*j\omega \mathbb {I} -{\mathbb {V} _{s}}=0$

求解 $\mathbb {I}$

$\mathbb {I} ={\frac {\mathbb {V} _{s}}{R+L*j\omega }}$

如果

$R+L*j\omega ={\sqrt {R^{2}+(L\omega )^{2}}}\angle arctan({\frac {L\omega }{R}})$

那么

$\mathbb {I} ={\frac {\mathbb {V} _{s}}{R+L*j\omega }}={\frac {V_{m}\angle \phi }{{\sqrt {R^{2}+(L\omega )^{2}}}\angle arctan({\frac {L\omega }{R}})}}={\frac {V_{m}}{\sqrt {R^{2}+(L\omega )^{2}}}}\angle (\phi -\angle arctan({\frac {L\omega }{R}}))$

为了便于理解上述定义，我们将引入两个新的符号来表示电流相量的幅值和相位。

$\mathbb {I} =I_{m}e^{j\alpha }$

那么

$I_{m}={\frac {V_{m}}{\sqrt {R^{2}+(L\omega )^{2}}}}$

以及

$\alpha =\phi -\angle arctan({\frac {L\omega }{R}})$

返回时域

$i(t)=\operatorname {Re} (\mathbb {I} e^{j\omega t})=\operatorname {Re} (I_{m}e^{j\alpha }e^{j\omega t})=\operatorname {Re} (I_{m}e^{j(\omega t+\alpha )})=I_{m}cos(\omega t+\alpha )$

$v_{R}(t)=R*i(t)$

$v_{L}(t)=L*{d \over dt}i(t)$

相量数值

RL电路的相量matlab解法.... m文件

时域

将端点方程代入回路方程得到：

$R*i(t)+L*{d \over dt}i(t)-V_{s}(t)=0$

$R=10$

$L=.01$

$\omega =377$

$V_{s}=\operatorname {Re} (120{\sqrt {2}}e^{j(377t+120^{\circ })})$

相量域

现在将方程变换到相量域..

${V_{s}}(t)\rightarrow {\mathbb {V} _{s}}=120{\sqrt {2}}\angle 120^{\circ }$

$V_{m}=120{\sqrt {2}}$

$\phi =\angle 120^{\circ }$

$\mathbb {I} ={\frac {\mathbb {V} _{s}}{R+L*j\omega }}={\frac {V_{m}}{\sqrt {R^{2}+(L\omega )^{2}}}}\angle (\phi -\angle arctan({\frac {L\omega }{R}}))=I_{m}e^{j\alpha }$

那么

$I_{m}={\frac {V_{m}}{\sqrt {R^{2}+(L\omega )^{2}}}}$

以及

$\alpha =\phi -\angle arctan({\frac {L\omega }{R}})$

回到时域

$\mathbb {I} =I_{m}e^{j\alpha }$

所以

$i(t)=\operatorname {Re} (15.9e^{j(377t+1.73)})=15.9cos(377t+1.73)$

$v_{R}(t)=R*i(t)=159cos(377t+1.73)$

$v_{L}(t)=L*{d \over dt}i(t)=-59.9sin(377t+1.73)$

检查

在 $t=0$ 时，电压是否加起来为零？

$159cos(1.73)-59.9sin(1.73)-120*{\sqrt {2}}cos(1.73)$

是的！… 可能是因为计算机的四舍五入误差，因为所有数值解都是近似值

拉普拉斯符号

时域

$R*i(t)+L*{d \over dt}i(t)-V_{s}(t)=0$

重写

$R*i(t)+L*{d \over dt}i(t)=V_{s}(t)$

拉普拉斯域

现在将两者都转换为拉普拉斯域…

${V_{s}}(t)\rightarrow {\mathcal {L}}\left\{{V_{s}}(t)\right\}$

$i(t)\rightarrow {\mathcal {L}}\left\{i(t)\right\}$

${d \over dt}i(t)\rightarrow s{\mathcal {L}}\left\{i(t)\right\}-i(0)\$

所以

$R*{\mathcal {L}}\left\{i(t)\right\}+L*(s{\mathcal {L}}\left\{i(t)\right\}-i(0))={\mathcal {L}}\left\{{V_{s}}(t)\right\}$

求解 ${\mathcal {L}}\left\{i(t)\right\}$

${\mathcal {L}}\left\{i(t)\right\}=$${\frac {{{\mathcal {L}}\left\{{V_{s}}(t)\right\}}+L*i(0)}{R+L*s}}$

至此，拉普拉斯符号解必须停止。接下来的步骤取决于 ${{\mathcal {L}}\left\{{V_{s}}(t)\right\}}$ 的形式。

返回时域

没有 ${{\mathcal {L}}\left\{{V_{s}}(t)\right\}}$ 就无法进行。函数 ${{\mathcal {L}}\left\{{V_{s}}(t)\right\}}$ 的形式决定了逆映射。

拉普拉斯数值解

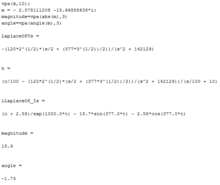matlab 拉普拉斯变换解法 .... m 文件

时域

将端点方程代入回路方程得到：

$R*i(t)+L*{d \over dt}i(t)-V_{s}(t)=0$

$R=10$

$L=.01$

$\omega =377$

$V_{s}=120{\sqrt {2}}cos(377t+120^{\circ })$

拉普拉斯域

现在转换为拉普拉斯域..

${V_{s}}(t)\rightarrow {\mathcal {L}}\left\{{V_{s}}(t)\right\}={\mathcal {L}}\left\{120{\sqrt {2}}cos(377t+120^{\circ })\right\}=-{\frac {(170.0*(0.5*s+326.0))}{(s^{2}+142129)}}$

${\mathcal {L}}\left\{i(t)\right\}={\frac {{\frac {-170.0*(0.5*s+326.0)}{(s^{2}+142129)}}+.01*i(0)}{10+.01*s}}$

回到时域

$i(t)={\mathcal {L}}^{-1}\left\{i(t)\right\}=(c+2.58)*e^{-{\frac {t}{.001}}}-15.7sin(377t)-2.58cos(377*t)$

将 cos 和 sin 项合并

$i(t)=15.9cos(377t+1.73)$

这与稳态（特解）相同。

必须等待特解来证明 C 为零以及 2.58 的来源。

16.7 毫秒的周期超过 5 个时间常数（5 毫秒）。这意味着在经历三分之一的振荡之前，99% 的初始能量不平衡已经消失。

sin 项必须为正，以便保持电感电压领先于电流的物理现实。有关此的更多讨论，请参见下面的相位检查。

模拟

上图中模拟的 Vs、VL 和 I 图。

周期检查

上面的周期看起来介于 16 毫秒和 17 毫秒之间，更接近 17 毫秒。这与以下公式一致

$\omega =2\pi *f$

$f={\frac {\omega }{2\pi }}$

$T={\frac {1}{f}}={\frac {2\pi }{\omega }}={\frac {2\pi }{377}}=16.7ms$

幅值检查

上面的 Vs 幅值看起来介于 150 伏和 200 伏之间，可能在 175 伏左右。这与以下数学计算一致

$120*{\sqrt {2}}=169.7$

i(t) 的幅值看起来介于 10 安培和 20 安培之间，更接近 15 安培。这与上面预测的 15.9 安培一致。

VL 的幅值看起来介于 0 伏和 100 伏之间，接近 50 伏。这与上面预测的 59.9 伏一致。

由于接地的选择，无法绘制 Vr。这在现实世界中也是如此。如果将接地放在电阻器和电感器之间，那么 Vr 和 VL 可以用示波器或上面的模拟器测量，但它们的相位关系将显示为$\pi$ 相位差。

瞬态响应检查

瞬态响应显然是模拟的一部分，因为所有值都从零开始，但到第一个周期结束时，值已经分开，并且在同一时间从不为零。将周期 16.7 毫秒与时间常数（在拉普拉斯反变换中与 C 相关的指数中看到）0.001 或 1 毫秒进行比较。在五个时间常数（2 毫秒）之后，瞬态响应小于其原始值 2.58（C 的值）的 99%。这意味着在第一个周期的 5/16.7 = 35% 的时间内，瞬态的值为

$2.58*e^{-2}=.35volts$

并在第一个周期结束时达到 0.0000001 伏。

相位检查

相位是描述计算中角度的词。电压始终领先于电感器中的电流（想想端子关系或 ELI），超前 $90^{\circ },{\frac {pi}{2}}$ 或 ${\frac {1}{4}}$ 个周期。

电感器的电压为橙色，电感器的电流位于上面底部的图形中。电压确实领先于电流。它们峰值之间的时间约为 4 毫秒，这大约是 ${\frac {1}{4}}$ 个周期 16.7 毫秒。

电阻器的电压在上面不可见，但它的相位与电流相同。源电压必须介于电阻器和电感器电压之间（来自基尔霍夫定律的回路）。它在上面。电路受电阻器支配（电压为 159，而 59 则为电感器电压），（电阻器为 10 欧姆，电感器为 0.01 * 377 = 3.77 欧姆），因此源电压更接近电阻器（电流波）。

功率分析

功率分析植根于相量域！相量域仅限于正弦驱动源。这就是为什么 RMS 功率及其计算的讨论不属于此分析的一部分。

$\mathbb {V} _{s}=120{\sqrt {2}}\angle 2.09$

$\mathbb {I} =15.9\angle 1.73$

$\mathbb {I} ^{*}=15.9\angle -1.73$

如果 :$\mathbb {V} =M_{v}\angle \phi _{v}\quad$，以及 $\quad \mathbb {I} =M_{i}\angle \phi _{i}$ 那么

$\mathbb {S} =\mathbb {V} \mathbb {I} ^{*}={\frac {M_{v}M_{i}}{2}}\angle (\phi _{v}-\phi _{i})={\frac {120{\sqrt {2}}*15.9}{2}}\angle (2.09-1.73)=135\angle 0.36=126+47.6j$

以及

$cos(.36)=.936$

总结

值	单位	描述
$135$	伏安 va	视在功率，公用事业公司管理的内容：他们设计的峰值功率，他们必须提供的峰值功率
$.936$	无量纲	功率因数，有功功率与视在功率之比，理想值为 1
$126$	瓦特 W	有功功率、平均功率、有效功率...消费者愿意支付的功率（瓦特小时）
$47.6$	无功功率 var	无功功率...为什么一个房间里的插座不能都在同一个断路器上

直观理解

ELI... 电压领先电流通过电感器

导数导致滞后...时间上的延迟...在正弦曲线中是正角度。