电路理论/传递函数目标

戴维南/诺顿阻抗完全表征了电路从负载的角度来看。微分方程完全描述了电路。电路的脉冲响应是使用卷积积分所需的全部信息。相量和复频完全描述了电路。即使在计算瞬态响应时，也出现了与稳态正弦响应相关的复频。它们之间有关系吗？是的。

目标是将上述所有内容理解为传递函数。为什么？大多数工程使用这个概念。以下是一些电气应用

目标是在电子学背景下介绍传递函数。

传递函数定义

传递函数是系统输出与系统输入之比。如果我们有一个输入函数 X(s) 和一个输出函数 Y(s)，我们定义传递函数 H(s) 为

H(s)={Y(s) \over X(s)}

在 RLC 电路中，传递函数是相量/复频/拉普拉斯域的概念。它们不是时域概念。它们独立于激励函数/源。有四种可能的 RLC 传递模式

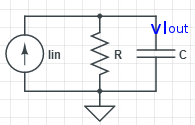传递函数有很多应用，我们很快就会看到。但它最直接的好处是消除了查找微分方程的必要性。回顾前面的例子

例子	微分方程	传递函数
卷积积分问题给定电压源，求总电流	: $v(t)=L{di(t) \over dt}+Ri(t)$	导纳: $H(s)={\frac {\mathbb {I} (s)}{\mathbb {V} (s)}}={\frac {1}{sL+R}}$
二阶，源激励求 i_o 给定 Is	$I_{s}={d^{2}i_{o} \over dt^{2}}+2{di_{o} \over dt}+2i_{o}$	分流 $H(s)={\frac {\mathbb {I} _{o}(s)}{\mathbb {I} _{s}(s)}}={\frac {\frac {1}{R+Ls}}{{\frac {1}{R+Ls}}+{\frac {1}{R}}+Cs}}$ $H(s)={\frac {\mathbb {I} _{o}(s)}{\mathbb {I} _{s}(s)}}={\frac {1}{s^{2}+2s+2}}$ R :=1; L :=1; C :=1; simplify((1/(R + Ls))/(1/(R + Ls) + 1/R + C*s))
二阶，源激励给定 V_s，求 V_cr	$V_{s}(t)=L{d({\frac {V_{CR}}{R}}) \over dt}+LC{d^{2}(V_{CR} \over dt^{2}})+V_{CR}$	分压器 $H(s)={\frac {\mathbb {V} _{cr}(s)}{\mathbb {V} _{s}(s)}}={\frac {\frac {1}{{\frac {1}{R}}+Cs}}{{\frac {1}{{\frac {1}{R}}+Cs}}+Ls}}$ $H(s)={\frac {1}{CLs^{2}+{\frac {Ls}{R}}+1}}$

找到传递函数后，下一步是找到时间常数或复频根，并根据这些推测解的形式。

齐次解是通过将传递函数的分母设置为零来找到的。对分母进行因式分解并找到复频根被称为找到“零点”。

分子（在所有上述例子中都是 1）可能有一个复频多项式（在复杂的电路中），它也可以被设置为零。根被称为“极点”。极点影响电路对不同频率的响应，而不是时域响应。

这标志着常规电路理论课程的结束。时域分析可以继续，在下例中有所提示。二战之前，为了用模拟计算机模拟物理系统，继续进行时域分析非常重要。但如今，数字计算机可以更精确地进行建模。因此，在此停止时域分析，并将进一步研究留给专门的课程。让我们总结一下我们在时域中关于电路的学习内容。

叠加原理允许将多个电源替换为一次一个电源（将其他电源归零），然后将所有电源的结果相加。
阻抗、导纳、分压器和分流器公式直接得出微分方程...这与相量/复频域和拉普拉斯变换域的数学相同。
卷积积分消除了将驱动函数（特别是正弦函数）转换为相量/复频域/拉普拉斯变换域的需要。相反，电源被替换为 1 伏或 1 安，特解变成一个直流最终条件（t = ∞），放在齐次解上，并在微分方程常数中出现。