控制系统/波德图

波德图

波德图是一个有用的工具，它显示了给定线性时不变 (LTI) 系统在不同频率下的增益和相位响应。波德图通常与给定系统的傅里叶变换一起使用。

波德幅值和相位图集的一个示例。幅值图通常位于顶部，相位图通常位于图集的底部。

波德图的频率绘制在对数频率轴上。频率轴上的每个刻度标记表示前一个值的 10 倍幂。例如，在标准波德图上，标记的值从 (0.1, 1, 10, 100, 1000, ...) 开始。因为每个刻度标记都是 10 的幂，所以它们被称为一个**十年**。请注意，随着您向右移动图表，十年的“长度”会减小。（注意，此描述与上图不符……每个十年有 10 个刻度标记，而不是一个，但由于它是对数图表，因此它们不是等间距的）。

波德幅值图用称为**分贝**的特殊单位测量系统的输入/输出比率。波德相位图测量相移，单位为度（通常，但也使用弧度）。

分贝

**分贝**是两个数字在对数刻度上的比率。要将两个数字（A 和 B）之间的比率表示为分贝，我们对表示幅值的数字应用以下公式（表示功率测量的数字使用因子 10 而不是 20）

$dB=20\log \left({A \over B}\right)$

其中 dB 是分贝结果。

或者，如果我们只想获取单个数字 C 的分贝值，我们可以很容易地写成

$dB=20\log(C)$

频率响应表示法

如果我们有一个系统传递函数 T(s)，我们可以将其分离成一个分子多项式 N(s) 和一个分母多项式 D(s)。我们可以这样写

$T(s)={\frac {N(s)}{D(s)}}$

为了获得幅值增益图，我们必须首先使用变量更改将传递函数转换为频率响应

$s=j\omega$

从这里，我们可以说我们的频率响应由两个部分组成，一个实部 R 和一个虚部 X

$T(j\omega )=R(\omega )+jX(\omega )$

我们将在下面使用这些形式。

直线逼近

波德幅值和相位图可以通过使用一系列直线快速轻松地近似。可以通过遵循一些简短、简单的规则（如下所列）来生成这些近似图。确定直线图后，实际的波德图是一条平滑的曲线，它遵循直线，并穿过**转折点**。

转折点

如果频率响应采用零极点形式

$T(j\omega )={\frac {\prod _{n}|j\omega +z_{n}|}{\prod _{m}|j\omega +p_{m}|}}$

我们说所有 z_n 和 p_m 的值称为波德图的**转折点**。这些是波德图方向发生最大变化的值。

转折点有时也称为“转折频率”、“截止点”或“拐点”。

波德增益图

**波德增益图**或**波德幅值图**显示每个输入频率下系统增益的比率。

波德增益计算

传递函数 T 的幅值定义为

$|T(j\omega )|={\sqrt {R^{2}+X^{2}}}$

然而，将“分子/分母”形式的函数转换为“实部+虚部”形式通常很困难。幸运的是，我们的分贝计算派上了用场。假设我们有一个频率响应，它被定义为一个分数，其分子和分母多项式定义为

$T(j\omega )={\frac {\prod _{n}|j\omega +z_{n}|}{\prod _{m}|j\omega +p_{m}|}}$

如果我们将两边都转换为分贝，则分贝计算中的对数会将参数的乘法转换为加法，并将除法转换为减法。

$Gain=\sum _{n}20\log(|j\omega +z_{n}|)-\sum _{m}20\log(|j\omega +p_{m}|)$

并且计算每一项的增益并将它们加在一起将给出系统在该频率下的增益。

博德增益近似

博德幅频图上直线的斜率以dB/十倍频程为单位测量，因为纵轴的单位是dB，横轴的单位是十倍频程。

ω = 0位于博德图的无限左侧（因为对数刻度永远不会达到零），因此在ω = 0处找到增益的值实际上将该值设置为从图的最左侧到第一个断点处的博德图的增益。ω = 0处直线的斜率值为0 dB/十倍频程。

从每个极点断点开始，直线的斜率下降20 dB/十倍频程。直线一直延伸到下一个断点。从每个零点断点开始，直线的斜率增加20 dB/十倍频程。重复极点和零点的双倍、三倍或更高倍数会使增益乘以相应的倍数。以下是一些示例

• 2个极点：-40 dB/十倍频程
• 10个极点：-200 dB/十倍频程
• 5个零点：+100 dB/十倍频程

博德相频图

博德相频图是系统输入频率特性相关的输入波形的相移图。同样，拉普拉斯变换不考虑系统的相移特性，但傅里叶变换可以。以“实部+虚部”形式表示的复函数的相位给出为

$\angle T(j\omega )=\tan ^{-1}\left({\frac {X}{R}}\right)$

博德图绘制过程

给定一个零极点形式的频率响应

$T(j\omega )=A{\frac {\prod _{n}|j\omega +z_{n}|}{\prod _{m}|j\omega +p_{m}|}}$

其中A是一个非零常数（可以是负数或正数）。

以下是绘制博德幅频图近似值的步骤

博德幅频图

步骤1

将传递函数分解为零极点形式。

步骤2

从传递函数中找到频率响应。

步骤3

使用对数将频率响应分离成分贝项的和

步骤4

使用$\omega =0$找到起始幅值。

步骤5

每个极点和每个零点的位置称为断点。在零点断点处，直线的斜率增加20dB/十倍频程。在极点处，直线的斜率减少20dB/十倍频程。

步骤6

在零点断点处，实际图的值与直线图的值相差3dB。零点比直线高3dB，极点比直线低3dB。

步骤7

将实际的博德图绘制成一条平滑曲线，使其遵循前一点的直线，并穿过断点。

以下是绘制博德相频图的步骤

博德相频图

步骤1

如果A为正，则从0度开始绘制图形（斜率为零）。如果A为负，则从180度（或-180度，它们是相同的）开始绘制图形，斜率为零。

步骤2

对于每个零点，当$\omega ={\frac {z_{n}}{10}}$（断频之前的一个十倍频程）时，将直线向上倾斜45度/十倍频程。多个零点意味着斜率更陡。

步骤3

对于每个极点，当$\omega ={\frac {p_{m}}{10}}$（断频之前的一个十倍频程）时，将直线向下倾斜45度/十倍频程。多个极点意味着斜率更陡。

步骤4

当相位变化了90度（对于零点）或-90度（对于极点）（或更大的值，对于多个极点或多个零点）时，再次使斜率变平。

示例

示例：恒定增益

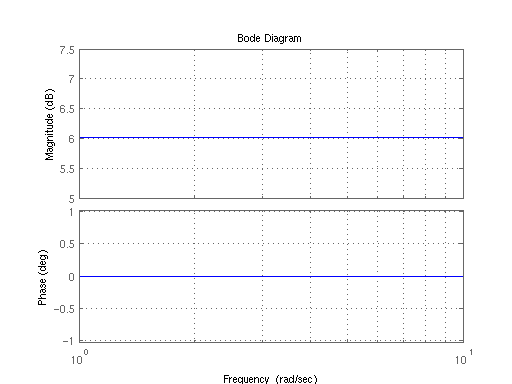
绘制一个放大器系统的博德图，该系统具有6dB的恒定增益增加。

因为增益值是恒定的，并且不依赖于频率，所以我们知道幅值图在图上的所有位置都是恒定的。没有断点，因此图的斜率永远不会改变。我们可以将图形绘制成一条位于6dB处的水平直线。

示例：积分器

绘制由以下传递函数给出的完美积分器系统的博德图：

$T(s)={\frac {2}{s}}$

首先，我们通过变量替换找到系统的频率响应：

$T(j\omega )={\frac {2}{j\omega }}$

然后我们将幅值转换为对数：

$Gain=20\log(2)-20\log(|j\omega |)$

注意，极点的断点位置位于 ω → 0，也就是图的最左边。此外，我们注意到将 0 代入 ω 会得到一个未定义的值（当极限趋近于负无穷大时）。我们知道，由于在零点有一个单极点，因此零点右边的图形（也就是所有地方）的斜率为 -20dB/十倍频程。通过将 ω → 1 代入幅值计算，我们可以确定第二项消失，此时幅值为 6dB。现在我们有了线的斜率和它与之相交的一个点，就可以绘制图形了。

示例：微分器

$T(j\omega )=2j\omega$

示例：一阶低通滤波器（1个断点）

$T(j\omega )={\frac {2.14}{j\omega +1}}$

进一步阅读

• 电路理论/博德图
• ControlTheoryPro.com 上的博德图

← 信号流图

控制系统

尼科尔斯图 →