信号流图 是另一种用来直观表示系统的图形方法。信号流图特别有用,因为它们允许使用特定的分析方法,比如 梅森增益公式。
信号流图通常使用曲线表示电线 和系统,而不是使用直角线和方框。每条曲线都被认为具有一个乘数值,这个值可以是恒定的增益值,也可以是整个传递函数。信号从曲线的一端传播到另一端,串联的曲线其总乘数值相乘(就像在框图中一样)。
信号流图帮助我们识别系统中被称为“回路”的结构,这些结构可以被单独分析以确定系统的完整响应。
 信号流图的示例。
信号流图的示例。
前向路径 是信号流图中连接输入和输出的路径,并且不超过任何单个节点或路径一次。单个系统可以有多个前向路径。
回路 是信号流图中返回自身的结构。回路不包含起点和终点,并且回路的终点与回路的起点是同一个节点。
如果回路共用一个节点或一条线,则称这些回路相交。
回路增益 是回路的总增益,即从一个点开始,绕回路一周,回到起点。
系统的增量值,用希腊字母 Δ 表示,计算如下

其中
- A 是所有单个回路增益的总和
- B 是所有不相交回路对的乘积之和
- C 是所有不相交回路三元组的乘积之和
- D 是所有不相交回路四元组的乘积之和
- 等等。
如果给定系统没有不相交的回路对,例如,B 和 B 后面的所有字母都将为零。
梅森公式 是确定系统增益的规则。梅森公式可以与框图一起使用,但它最常(最容易)与信号流图一起使用。
如果我们已经计算出增量值(上面),那么我们可以使用 梅森增益规则 来找到系统的完整增益

其中 M 是系统的总增益,表示为系统输出增益 (yout) 与输入增益 (yin) 的比率。Mk 是第 kth 个前向路径的增益,Δk 是第 kth 个回路的回路增益。
通过系统简化解决信号流图 : 两个相互交织的回路
[编辑 | 编辑源代码]此示例展示了如何使用系统化约简规则求解包含五个未知数的五个方程组。自变量为  。因变量为
。因变量为  ,
, ,
, ,
, ,
, 。系数分别标记为
。系数分别标记为  。
。
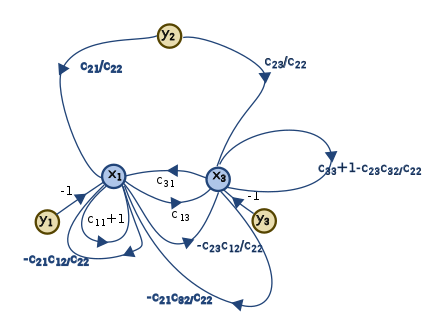
以下是起始信号流图


求解  的步骤如下。
的步骤如下。
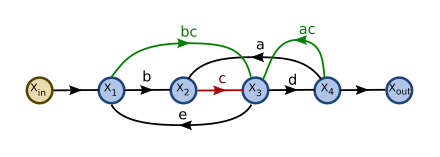


 没有输出流,也不是感兴趣的节点。
没有输出流,也不是感兴趣的节点。 

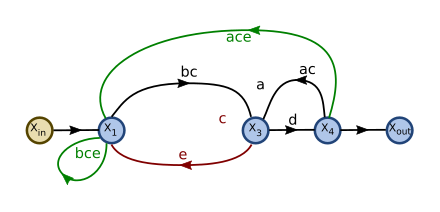



节点  没有输出流,也不是感兴趣的节点。它将与其输入流一起被删除。
没有输出流,也不是感兴趣的节点。它将与其输入流一起被删除。







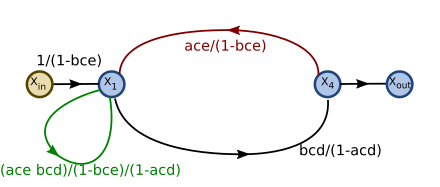


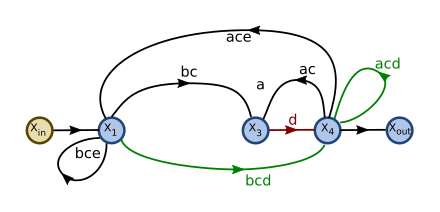
 的输出则被消除:
的输出则被消除: 直接连接到
直接连接到  ,使用两条替换边增益的乘积。
,使用两条替换边增益的乘积。
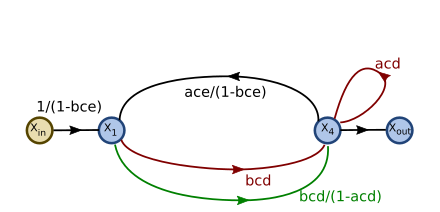
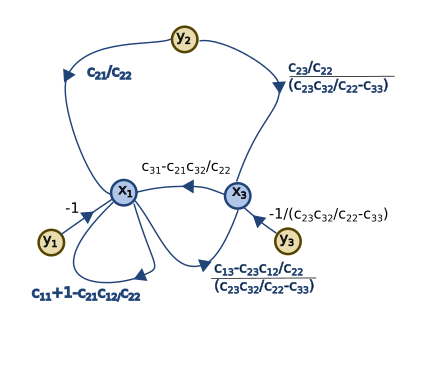
 不是一个感兴趣的变量;因此,它的节点及其输入被消除。
不是一个感兴趣的变量;因此,它的节点及其输入被消除。






 不是感兴趣的变量;
不是感兴趣的变量; 及其流入被消除
及其流入被消除




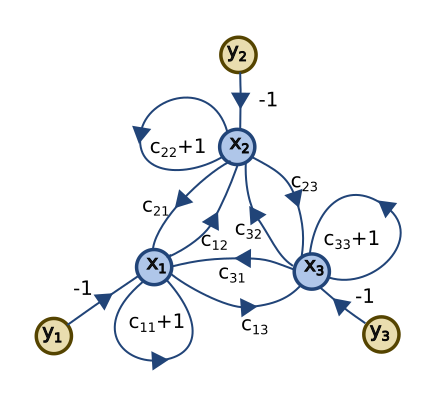
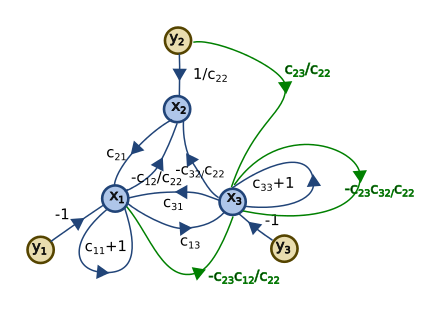
这个例子展示了如何使用系统缩减规则求解三个方程三个未知数的系统。
自变量是  ,
, ,
, 。因变量是
。因变量是  ,
, ,
, 。系数标记为
。系数标记为  。求解
。求解  的步骤如下
的步骤如下








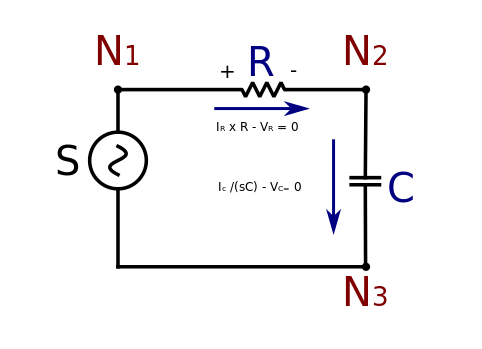
此插图展示了电路的物理连接。独立电压源 S 与电阻器 R 和电容器 C 串联连接。该示例从物理电路方程发展而来,并使用信号流图技术求解。极性很重要
- S 是一个电源,正极端子位于 N1,负极端子位于 N3
- R 是一个电阻器,正极端子位于 N1,负极端子位于 N2
- C 是一个电容器,正极端子位于 N2,负极端子位于 N3。
感兴趣的未知变量是电容器 C 两端的电压。
解决方案方法
- 从物理网络中找到方程组。这些方程本质上是无因果的。
- 电容器和电阻器的支路方程。方程将使用拉普拉斯变换作为传递函数开发。
- 基尔霍夫电压定律和电流定律
- 根据方程构建信号流图。
- 求解信号流图。
 展示了 R 和 C 的支路方程。
展示了 R 和 C 的支路方程。
电阻器 R (分支方程  )
)
[编辑 | 编辑源代码]电阻器在时域中的分支方程为

在拉普拉斯变换后的信号空间中

电容器 C (分支方程  )
)
[编辑 | 编辑源代码]电容器在时域中的分支方程为

假设电容器最初是放电的,则该方程变为

对方程求导并乘以C,得到导数形式

在拉普拉斯变换后的信号空间中

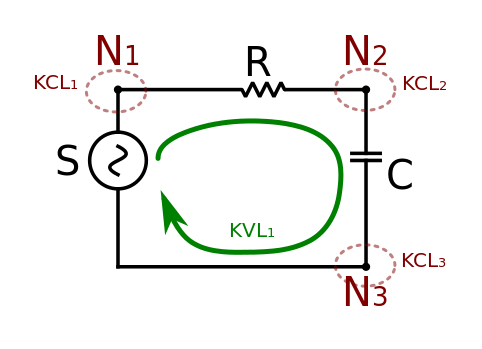
基尔霍夫电压定律方程 
[编辑 | 编辑源代码]该电路只有一个独立回路。其在时域中的方程为

在拉普拉斯变换后的信号空间中

基尔霍夫电流定律方程 
[编辑 | 编辑源代码]该电路具有三个节点,因此有三个基尔霍夫电流方程(此处表示为从节点流出的电流)。

在拉普拉斯变换后的信号空间中

必须选择一组独立的方程。对于电流定律,需要删除其中一个方程。在本例中,让我们选择  。
。
然后我们查看方程清单以及每个方程所关联的信号。
| 方程 |
信号 |

|

|

|

|

|

|

|

|

|

|
下一步是为每个方程分配一个信号,该信号将表示为一个节点。每个独立的源信号在信号流图中表示为一个源节点,因此没有方程分配给独立的源信号 。从这组方程中可以得到许多有效的信号流图。每个方程只能使用一次,并且必须表示感兴趣的变量。
。从这组方程中可以得到许多有效的信号流图。每个方程只能使用一次,并且必须表示感兴趣的变量。
| 方程 |
信号 |
分配的信号节点 |

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

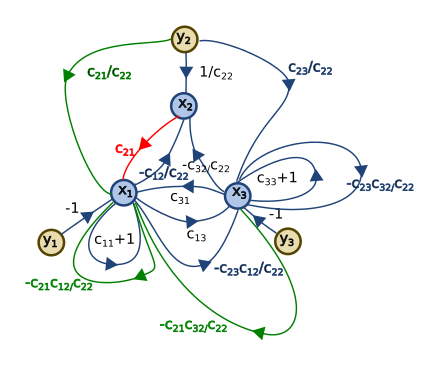
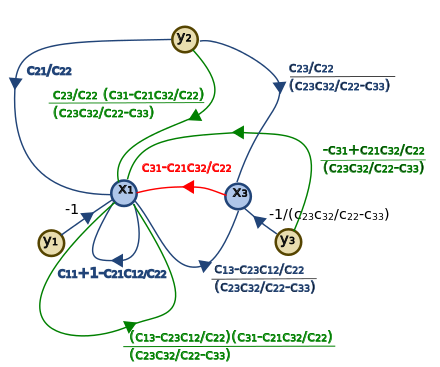
下一步是求解信号流图。
使用 Mason 或系统简化,得到的信号流图是

 角度位置伺服和信号流图。θC = 期望角度指令,θL = 实际负载角度,KP = 位置环路增益,VωC = 速度指令,VωM = 电机速度感应电压,KV = 速度环路增益,VIC = 电流指令,VIM = 电流感应电压,KC = 电流环路增益,VA = 功率放大器输出电压,LM = 电机电感,VM = 电机电感上的电压,IM = 电机电流,RM = 电机电阻,RS = 电流感应电阻,KM = 电机转矩常数 (Nm/amp) ,T = 转矩,M = 所有旋转部件的惯性矩 α = 角加速度,ω = 角速度,β = 机械阻尼,GM = 电机反电动势常数,GT = 测速计转换增益常数。有一个前向路径(以不同的颜色显示)和六个反馈回路。驱动轴被认为足够坚固,不需要作为弹簧处理。常数以黑色显示,变量以紫色显示。
角度位置伺服和信号流图。θC = 期望角度指令,θL = 实际负载角度,KP = 位置环路增益,VωC = 速度指令,VωM = 电机速度感应电压,KV = 速度环路增益,VIC = 电流指令,VIM = 电流感应电压,KC = 电流环路增益,VA = 功率放大器输出电压,LM = 电机电感,VM = 电机电感上的电压,IM = 电机电流,RM = 电机电阻,RS = 电流感应电阻,KM = 电机转矩常数 (Nm/amp) ,T = 转矩,M = 所有旋转部件的惯性矩 α = 角加速度,ω = 角速度,β = 机械阻尼,GM = 电机反电动势常数,GT = 测速计转换增益常数。有一个前向路径(以不同的颜色显示)和六个反馈回路。驱动轴被认为足够坚固,不需要作为弹簧处理。常数以黑色显示,变量以紫色显示。

































































































